Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều, một tài liệu ôn tập vô cùng quan trọng dành cho học sinh lớp 7. Đề thi này được biên soạn theo chương trình sách giáo khoa Cánh diều, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Với đề thi này, các em có thể tự đánh giá năng lực của mình, xác định những kiến thức còn yếu và tập trung ôn luyện để đạt kết quả tốt nhất trong kỳ thi sắp tới.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1.D | 2.C | 3.C | 4.D | 5.C | 6.A | 7.D | 8.C | 9.C | 10.D |
Câu 1
Phương pháp:
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
Tập hợp các số hữu tỉ được kí hiệu là \(\mathbb{Q}\).
Cách giải:
Ta có:
+ \(\frac{1}{2} \in \mathbb{Q}\) nên phương án A. \(\frac{1}{2} \notin \mathbb{Q}\)là sai do đó, loại đáp án A.
+ \(\frac{{ - 8}}{0}\) không đúng với dạng số hữu tỉ (do mẫu số bằng \(0\)) nên phương án B. \(\frac{{ - 8}}{0} \in \mathbb{Q}\)là sai do đó, loại đáp án B.
+ \(5 = \frac{5}{1}\) là một số hữu tỉ và \(5 \in \mathbb{Q}\) nên phương án C. \(5 \notin \mathbb{Q}\) là sai do đó, loại đáp án C.
+ \(\frac{4}{{ - 5}}\) là một số hữu tỉ nên \(\frac{4}{{ - 5}} \in \mathbb{Q}\)do đó, phương án D đúng.
Chọn D.
Câu 2
Phương pháp:
Tính lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Tính tích của hai lũy thừa cùng cơ số: Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
Cách giải:
\({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\)\( = {\left( {0,3} \right)^{3.4}}.{\left( {0,3} \right)^3} = {\left( {0,3} \right)^{12}}.{\left( {0,3} \right)^3} = {\left( {0,3} \right)^{12 + 3}} = {\left( {0,3} \right)^{15}}\)
Chọn C.
Câu 3
Phương pháp:
Đổi hỗn số sang phân số, từ phân số đổi sang số thập phân.
Tính căn bậc hai của một số.
Tính giá trị tuyệt đối của một số.
So sánh các số để sắp xếp thứ tự tăng dần của các số.
Cách giải:
Ta có:
\(\begin{array}{l}2\frac{1}{4} = \frac{9}{4} = 2,25\\\sqrt {16} = \sqrt {{4^2}} = 4\\ - \left| { - \sqrt {196} } \right| = - \left| {\sqrt {196} } \right| = - \sqrt {196} \end{array}\)
*Vì \(2,25 < 4\) nên \(2\frac{1}{4} < \sqrt {16} \) (*)
*Vì \(83 < 196\) nên \(\sqrt {83} < \sqrt {196} \) suy ra \( - \sqrt {83} > - \sqrt {196} \) hay \( - \sqrt {83} > - \left| { - \sqrt {196} } \right|\) (1)
Vì \(0,0\left( {51} \right) < 1 = \sqrt 1 < \sqrt {83} \) suy ra \( - \sqrt {83} < - 1 < - 0,0\left( {51} \right)\) (2)
Từ (1) và (2), suy ra \( - \left| { - \sqrt {196} } \right| < - \sqrt {83} < - 0,0\left( {51} \right)\) (**)
Từ (*) và (**), suy ra \( - \left| { - \sqrt {196} } \right| < - \sqrt {83} < - 0,0\left( {51} \right) < 2\frac{1}{4} < \sqrt {16} \)
Vậy thứ tự tăng dần của các số là: \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\frac{1}{4}\,\,;\,\,\sqrt {16} .\)
Chọn C.
Câu 4
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{4} = \frac{y}{{ - 7}} = \frac{{x - y}}{{4 - \left( { - 7} \right)}} = \frac{{33}}{{11}} = 3\)
Khi đó, \(\frac{x}{4} = 3\) suy ra \(x = 4.3 = 12\)
\(\frac{y}{{ - 7}} = 3\) suy ra \(y = - 7.3 = - 21\)
Vậy \(x = 12;y = - 21\).
Chọn D.
Câu 5
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: \(\frac{a}{b} = \frac{c}{d}\) suy ra \(\frac{a}{b} = \frac{c}{d} = \frac{{2c}}{{2d}}\) hay \(\frac{a}{b} = \frac{{2c}}{{2d}} = \frac{{a + 2c}}{{b + 2d}}\) (1) (tính chất của dãy tỉ số bằng nhau)
Mặt khác, suy ra \(\frac{a}{b} = \frac{c}{d} = \frac{{2a}}{{2b}}\) hay \(\frac{a}{b} = \frac{c}{d} = \frac{{2a - c}}{{2b - d}}\) (2) (tính chất của dãy tỉ số bằng nhau)
Từ (1) và (2) suy ra \(\frac{{a + 2c}}{{b + 2d}} = \frac{{2a - c}}{{2b - d}}\)
Do đó, đáp án C đúng.
Chọn C.
Câu 6
Phương pháp:
Gọi số tiền (triệu đồng) được chia của An và Bình lần lượt là \(x\) và \(y\) (điều kiện: \(x > 0,y > 0\))
Xác định hai đại lượng tỉ lệ thuận, lập tỉ lệ thức.
Áp dụng tính chất của dãy tỉ số bằng nhau, tìm \(x\) và \(y\).
Cách giải:
Gọi số tiền (triệu đồng) được chia của An và Bình lần lượt là \(x\) và \(y\) (điều kiện: \(x > 0,y > 0\))
Do số tiền và số gà nuôi của hai bạn là hai đại lượng tỉ lệ thuận với nhau nên ta có: \(\frac{x}{{10}} = \frac{y}{8}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{10}} = \frac{y}{8} = \frac{{x + y}}{{10 + 8}} = \frac{{3,6}}{{18}} = \frac{1}{5}\)
Khi đó, \(\frac{x}{{10}} = \frac{1}{5}\) suy ra \(x = 10.\frac{1}{5} = 2\,\left( {tm} \right)\)
\(\frac{y}{8} = \frac{1}{5}\) suy ra \(y = 8.\frac{1}{5} = 1,6\,\left( {tm} \right)\)
Vậy An nhận được 2 triệu đồng và Bình nhận được 1,6 triệu đồng.
Chọn A.
Câu 7
Phương pháp:
Diện tích xung quanh của hình lập phương có một cạnh là \(a\): \({S_{xq}} = 4{a^2}\).
Diện tích hình vuông có độ dài một cạnh là \(a\): \(S = {a^2}\)
Cách giải:
Diện tích tấm bìa tạo thành con xúc xắc đó bao gồm diện tích xung quanh của hình lập phương và tổng diện tích hai mặt đáy của hình lập phương.
Vậy diện tích tấm bìa tạo thành con xúc xắc là:
\({4.5^2} + {2.5^2} = 150\,\left( {c{m^2}} \right)\)
Chọn D.
Câu 8
Phương pháp:
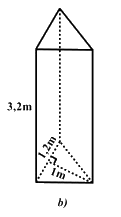
Thể tích của hình lăng trụ đứng tam giác: \(V = S\)đáy\(.h\)
Cách giải:
Thể tích của gàu xúc hình lăng trụ đứng tam giác là: \(V = S\)đáy\(.h = \frac{1}{2}.1.1,2.3,2 = 1,92\,\left( {{m^3}} \right)\)
Ta có: \(\frac{{40}}{{1,92}} = \frac{{125}}{6} \approx 20,8\left( 3 \right)\)
Vậy xe phải xúc ít nhất \(21\) gàu để hết \(40{m^3}\) cát.
Chọn C.
Câu 9
Phương pháp:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Cách giải:
Từ các hình vẽ, ta nhận thấy Hình 3 là hình vẽ của hai góc đối đỉnh.
Chọn C.
Câu 10
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Cách giải:
Vì \(yy'//zz'\) nên \(\angle xAy' = \angle xBz' = {60^0}\) (hai góc đồng vị)
Vì \(\angle xBz'\) và \(\angle zBx'\) là hai đối đỉnh nên \(\angle xBz' = \angle zBx' = {60^0}\).
Vậy \(\angle zBx' = {60^0}\)
Chọn D.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
a) Đổi hỗn số sang phân số.
Thực hiện các phép toán với số hữu tỉ.
b) Tích và thương của hai lũy thừa cùng cơ số:
+ Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
+ Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\)
Lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Tính \({\left( {a.b} \right)^m} = {a^m}.{b^m}\)
c) Tính căn bậc hai số học của một số thực
Thực hiện các phép toán với số hữu tỉ.
d) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) \(\left( {2\frac{5}{6} + 1\frac{4}{9}} \right):\left( {10\frac{1}{{12}} - 9,5} \right)\)
\(\begin{array}{l} = \left( {\frac{{17}}{6} + \frac{{13}}{9}} \right):\left( {\frac{{121}}{{12}} - \frac{{19}}{2}} \right)\\ = \left( {\frac{{51}}{{18}} + \frac{{26}}{{18}}} \right):\left( {\frac{{121}}{{12}} - \frac{{114}}{{12}}} \right)\\ = \frac{{77}}{{18}}:\frac{7}{{12}} = \frac{{77}}{{18}}.\frac{{12}}{7}\\ = \frac{{22}}{3}\end{array}\)
b) \(\frac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
\(\begin{array}{l} = \frac{{{{\left( {{2^5}} \right)}^3}.{{\left( {{3^2}} \right)}^5}}}{{{{\left( {{2^3}} \right)}^3}.{{\left( {2.3} \right)}^6}}} = \frac{{{2^{5.3}}{{.3}^{2.5}}}}{{{2^{3.3}}{{.2}^6}{{.3}^6}}}\\ = \frac{{{2^{15}}{{.3}^{10}}}}{{{2^9}{{.2}^6}{{.3}^6}}} = \frac{{{2^{15}}{{.3}^{10}}}}{{{2^{9 + 6}}{{.3}^6}}}\\ = \frac{{{2^{15}}{{.3}^{10}}}}{{{2^{15}}{{.3}^6}}} = \frac{{{3^{10}}}}{{{3^6}}}\\ = {3^{10 - 6}} = {3^4} = 81\end{array}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\frac{{25}}{{16}}} \)
\(\begin{array}{l} = \sqrt {{8^2}} + 2.\sqrt {{3^2}} - 8.\sqrt {{{\left( {\frac{5}{4}} \right)}^2}} \\ = 8 + 2.3 - 8.\frac{5}{4}\\ = 8 + 6 - 10\\ = 4\end{array}\)
d) \(\left| {\frac{1}{{ - 5}}} \right| - \frac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \frac{{\left| 2 \right|}}{5}\)
\(\begin{array}{l} = \frac{1}{5} - \frac{4}{5} - \frac{2}{5}\\ = \frac{{ - 5}}{5} = - 1\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
b) Biến đổi về dạng \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\)
c) Tính căn bậc hai số học của số thực
Đổi hỗn số sang phân số
Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(x - \frac{1}{2} = 3\frac{1}{2}:\frac{7}{2}\)
\(\begin{array}{l}x - \frac{1}{2} = \frac{7}{2}:\frac{7}{2}\\x - \frac{1}{2} = \frac{7}{2}.\frac{2}{7} = 1\\x = 1 + \frac{1}{2} = \frac{2}{2} + \frac{1}{2}\\x = \frac{3}{2}\end{array}\)
Vậy \(x = \frac{3}{2}\)
b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
\(\begin{array}{l}{3^{ - 1 + x}} + {5.3^{x - 1}} = 162\\{3^{x - 1}}.\left( {1 + 5} \right) = 162\\{3^{x - 1}}.6 = 162\\{3^{x - 1}} = 162:6\\{3^{x - 1}} = 27\\{3^{x - 1}} = {3^3}\\ \Rightarrow x - 1 = 3\\\,\,\,\,\,\,\,x = 3 + 1\end{array}\)
\(x = 4\) (thỏa mãn \(x\) là số nguyên)
Vậy \(x = 4\)
c) \(\sqrt {1,96} + 3\frac{x}{4} = \sqrt {0,04} + \frac{1}{4}.\sqrt {{{\left( {\frac{{89}}{5}} \right)}^2}} \)
\(\begin{array}{l}\sqrt {{{\left( {1,4} \right)}^2}} + \frac{{12 + x}}{4} = \sqrt {{{\left( {0,2} \right)}^2}} + \frac{1}{4}.\frac{{89}}{5}\\1,4 + \frac{{12 + x}}{4} = 0,2 + \frac{{89}}{{20}}\\\frac{{12 + x}}{4} = 0,2 + \frac{{89}}{{20}} - 1,4\\\frac{{12 + x}}{4} = \frac{4}{{20}} + \frac{{89}}{{20}} - \frac{{28}}{{20}}\\\frac{{12 + x}}{4} = \frac{{13}}{4}\\ \Rightarrow 12 + x = 13\\\,\,\,\,\,\,\,x = 13 - 12\\\,\,\,\,\,\,\,x = 1\end{array}\)
Vậy \(x = 1\)
d) \(\left| {2x:\frac{4}{5} - \frac{{1,6}}{4}} \right| = \frac{7}{5}\)
\(\left| {2x:\frac{4}{5} - \frac{2}{5}} \right| = \frac{7}{5}\)
Trường hợp 1:
\(\begin{array}{l}2x:\frac{4}{5} - \frac{2}{5} = \frac{7}{5}\\2x:\frac{4}{5} = \frac{7}{5} + \frac{2}{5}\\2x:\frac{4}{5} = \frac{9}{5}\\2x = \frac{9}{5}.\frac{4}{5} = \frac{{36}}{{25}}\\x = \frac{{36}}{{25}}:2 = \frac{{36}}{{25}}.\frac{1}{2}\\x = \frac{{18}}{{25}}\end{array}\)
Vậy \(x \in \left\{ {\frac{{18}}{{25}};\frac{{ - 2}}{5}} \right\}\)
Trường hợp 2:
\(\begin{array}{l}2x:\frac{4}{5} - \frac{2}{5} = \frac{{ - 7}}{5}\\2x:\frac{4}{5} = \frac{{ - 7}}{5} + \frac{2}{5}\\2x:\frac{4}{5} = \frac{{ - 5}}{5} = - 1\\2x = - 1.\frac{4}{5} = \frac{{ - 4}}{5}\\x = \frac{{ - 4}}{5}:2 = \frac{{ - 4}}{5}.\frac{1}{2}\\x = \frac{{ - 2}}{5}\end{array}\)
Bài 3
Phương pháp:
Gọi số học sinh của lớp 7A, 7B, 7C lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Xác định hai đại lượng tỉ lệ nghịch, lập tỉ lệ thức.
Áp dụng tính chất của dãy tỉ số bằng nhau, tìm \(x,y,z\).
Cách giải:
Gọi số học sinh của lớp 7A, 7B, 7C lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Do với khối lượng công việc như nhau thì số học sinh và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên \(3x = 4y = 5z\) suy ra \(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{4}}} = \frac{z}{{\frac{1}{5}}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{4}}} = \frac{z}{{\frac{1}{5}}} = \frac{{x + y + z}}{{\frac{1}{3} + \frac{1}{4} + \frac{1}{5}}} = \frac{{94}}{{\frac{{47}}{{60}}}} = 120\)
Do đó, \(\frac{x}{{\frac{1}{3}}} = 120\) suy ra \(x = \frac{1}{3}.120 = 40\,\) (tm \(x \in {\mathbb{N}^*}\))
\(\frac{y}{{\frac{1}{4}}} = 120\) suy ra \(x = \frac{1}{4}.120 = 30\) (tm \(y \in {\mathbb{N}^*}\))
\(\frac{z}{{\frac{1}{5}}} = 120\) suy ra \(z = \frac{1}{5}.120 = 24\) (tm \(z \in {\mathbb{N}^*}\))
Vậy số học sinh của lớp 7A, 7B, 7C lần lượt là 40 học sinh, 30 học sinh, 24 học sinh.
Bài 4
Phương pháp:
a) Thể tích của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c:V = abc\)
b) Diện tích bìa cứng dùng để là hộp bao gồm diện tích xung quanh và tổng diện tích hai đáy của hộp.
Diện tích xung quanh của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\): \({S_{xq}} = 2.\left( {a + b} \right).c\)
Diện tích hình chữ nhật có chiều dài là \(a\), chiều rộng đáy là \(b\): \(S = ab\)
Cách giải:
a) Thể tích của hộp là: \(22.11.9 = 2178\,\left( {c{m^3}} \right)\)
b) Diện tích bìa cứng dùng để là hộp bao gồm diện tích xung quanh và tổng diện tích hai đáy của hộp.
Diện tích xung quanh của hộp là: \({S_{xq}} = 2.\left( {22 + 11} \right).9 = 594\,\left( {c{m^2}} \right)\)
Diện tích hai đáy của hộp là: \(S = 2.22.11 = 484\,\left( {c{m^2}} \right)\)
Diện tích bìa cứng dùng để làm hộp là: \({S_{xq}} + S = 594 + 484 = 1078\,\left( {c{m^2}} \right)\)
Bài 5
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}} = \frac{{a - b}}{{2020 - 2021}} = \frac{{b - c}}{{2021 - 2022}} = \frac{{c - a}}{{2022 - 2020}}\)
Suy ra \(\frac{{a - b}}{{ - 1}} = \frac{{b - c}}{{ - 1}} = \frac{{c - a}}{2}\) hay \(c - a = - 2\left( {a - b} \right) = - 2\left( {b - c} \right)\)
Do đó, \(\left( {c - a} \right).\left( {c - a} \right) = \left[ { - 2\left( {a - b} \right)} \right].\left[ { - 2\left( {b - c} \right)} \right]\)
Suy ra \({\left( {c - a} \right)^2} = 4\left( {a - b} \right)\left( {b - c} \right)\) (đpcm)
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Chọn phương án đúng?
A. \(\frac{1}{2} \notin \mathbb{Q}\)
B. \(\frac{{ - 8}}{0} \in \mathbb{Q}\)
C. \(5 \notin \mathbb{Q}\)
D. \(\frac{4}{{ - 5}} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\) là:
A. \({\left( {0,3} \right)^4}\)
B. \({\left( {0,3} \right)^{10}}\)
C. \({\left( {0,3} \right)^{15}}\)
D. \({\left( {0,3} \right)^{12}}\)
Câu 3: Sắp xếp các số sau theo thứ tự tăng dần: \(2\frac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
A. \(2\frac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
B. \(\sqrt {16} \,\,;\,\,2\frac{1}{4}\,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,\,\, - \sqrt {83} \,\,;\, - \left| { - \sqrt {196} } \right|\,.\)
C. \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\frac{1}{4}\,\,;\,\,\sqrt {16} .\)
D. \(\sqrt {16} \,\,;\,\,2\frac{1}{4}\,\,;\,\,\, - 0,0\left( {51} \right)\,\,;\,\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,.\)
Câu 4: Tìm hai số \(x;y\) biết: \(\frac{x}{4} = \frac{y}{{ - 7}}\) và \(x - y = 33\).
A. \(x = 10;y = - 23\)
B. \(x = 24;y = - 9\)
C. \(x = 15;y = - 18\)
D. \(x = 12;y = - 21\)
Câu 5: Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\), ta có thể suy ra được tỉ lệ nào trong các đáp án sau:
A. \(\frac{a}{c} = \frac{d}{b}\)
B. \(\frac{a}{b} = \frac{c}{d} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}}\)
C. \(\frac{{a + 2c}}{{b + 2d}} = \frac{{2a - c}}{{2b - d}}\)
D. \(\frac{{a + 5}}{{b + 5}} = \frac{{c + 5}}{{d + 5}}\)
Câu 6: An và Bình cùng nhau nuôi gà, An nuôi 10 con, Bình nuôi 8 con. Sau khi bán hết số gà thu được tổng cộng 3,6 triệu đồng, hai bạn quyết định số tiền tỉ lệ với số con gà mỗi bạn đã nuôi. Tính số tiền mỗi bạn nhận được.
A. An nhận được 2 triệu đồng và Bình nhận được 1,6 triệu đồng.
B. An nhận được 1,6 triệu đồng và Bình nhận được 2 triệu đồng.
C. An nhận được 2,4 triệu đồng và Bình nhận được 1,2 triệu đồng.
D. An nhận được 1,2 triệu đồng và Bình nhận được 2,4 triệu đồng.
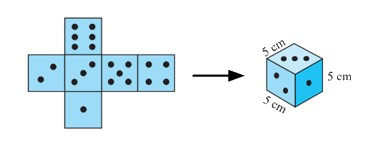
Câu 7: Bạn Lan làm một con xúc xắc hình lập phương từ tấm bìa có kích thước như hình vẽ bên dưới.
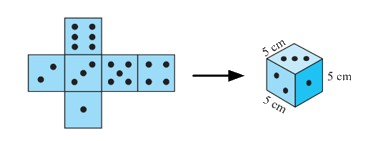
Diện tích tấm bìa tạo thành con xúc xắc đó là bao nhiêu?
A. \(100c{m^2}\)
B. \(125c{m^2}\)
C. \(136c{m^2}\)
D. \(150c{m^2}\)
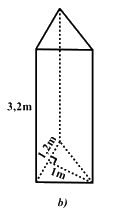
Câu 8: Gàu xúc của một xe xúc (Hình a) có dạng gần như một hình lăng trụ đứng tam giác với các kích thước đã cho ở hình b). Để xúc hết \(40{m^3}\) cát, xe phải xúc ít nhất bao nhiêu gàu?
A. \(19\)gàu
B. \(20\,\)gàu
C. \(21\) gàu
D. \(22\)gàu
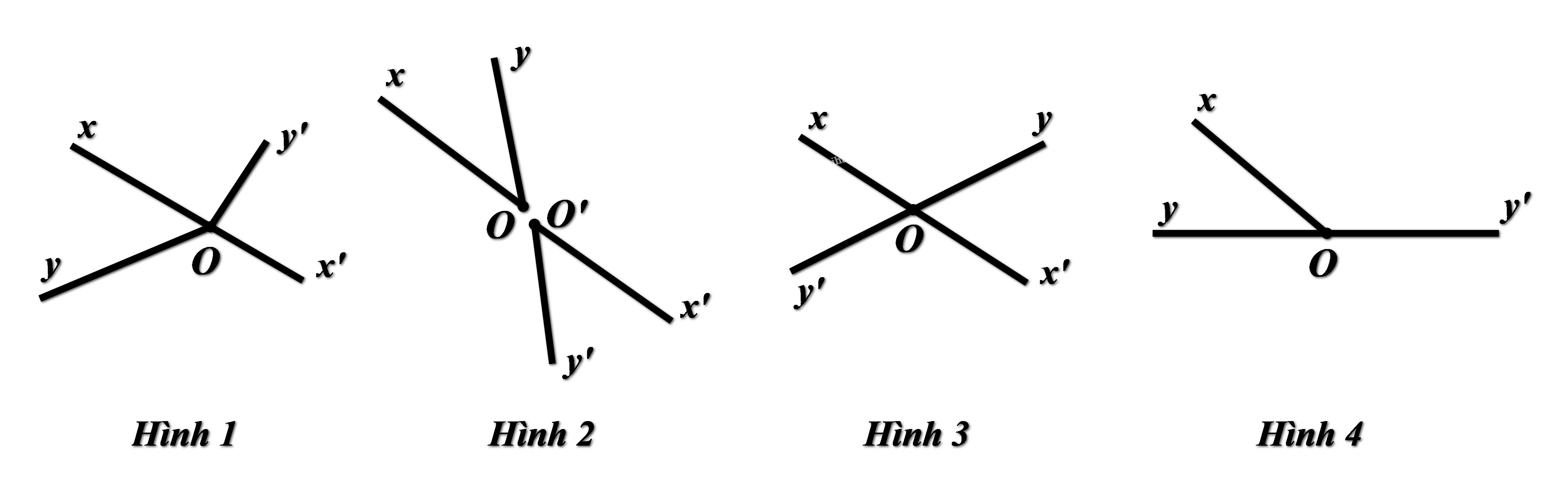
Câu 9: Hai góc nào dưới đây là hai góc đối đỉnh?
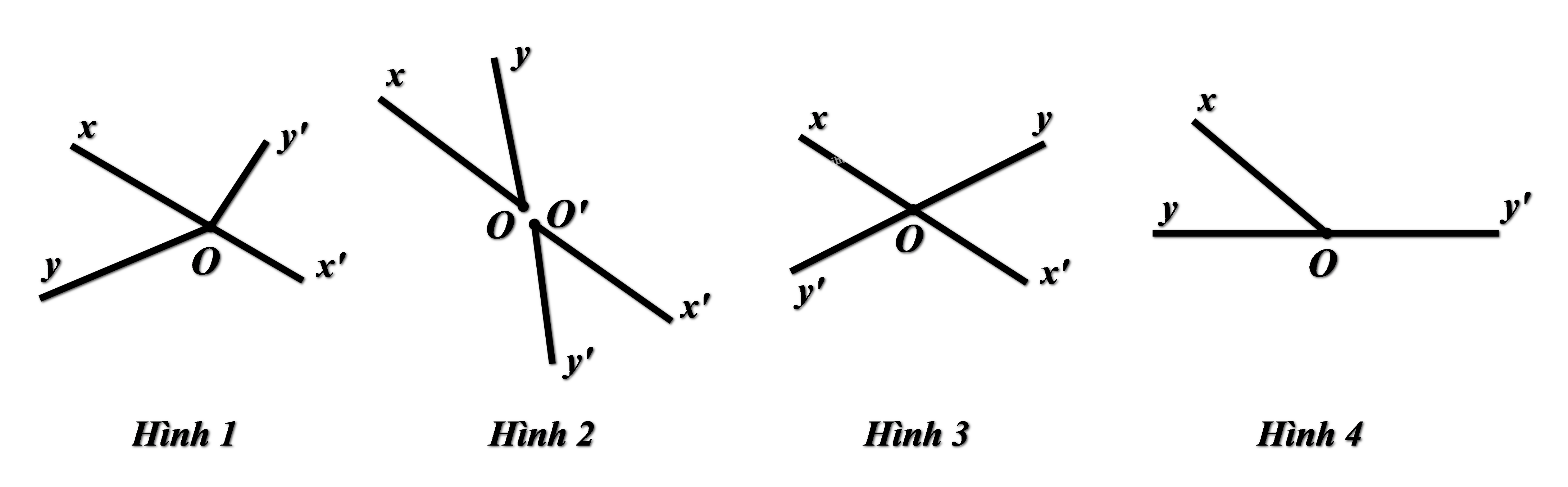
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 10: Cho hình vẽ bên dưới, biết \(yy'//zz',\angle xAy' = {60^0}\). Tính số đo của \(\angle zBx'.\)
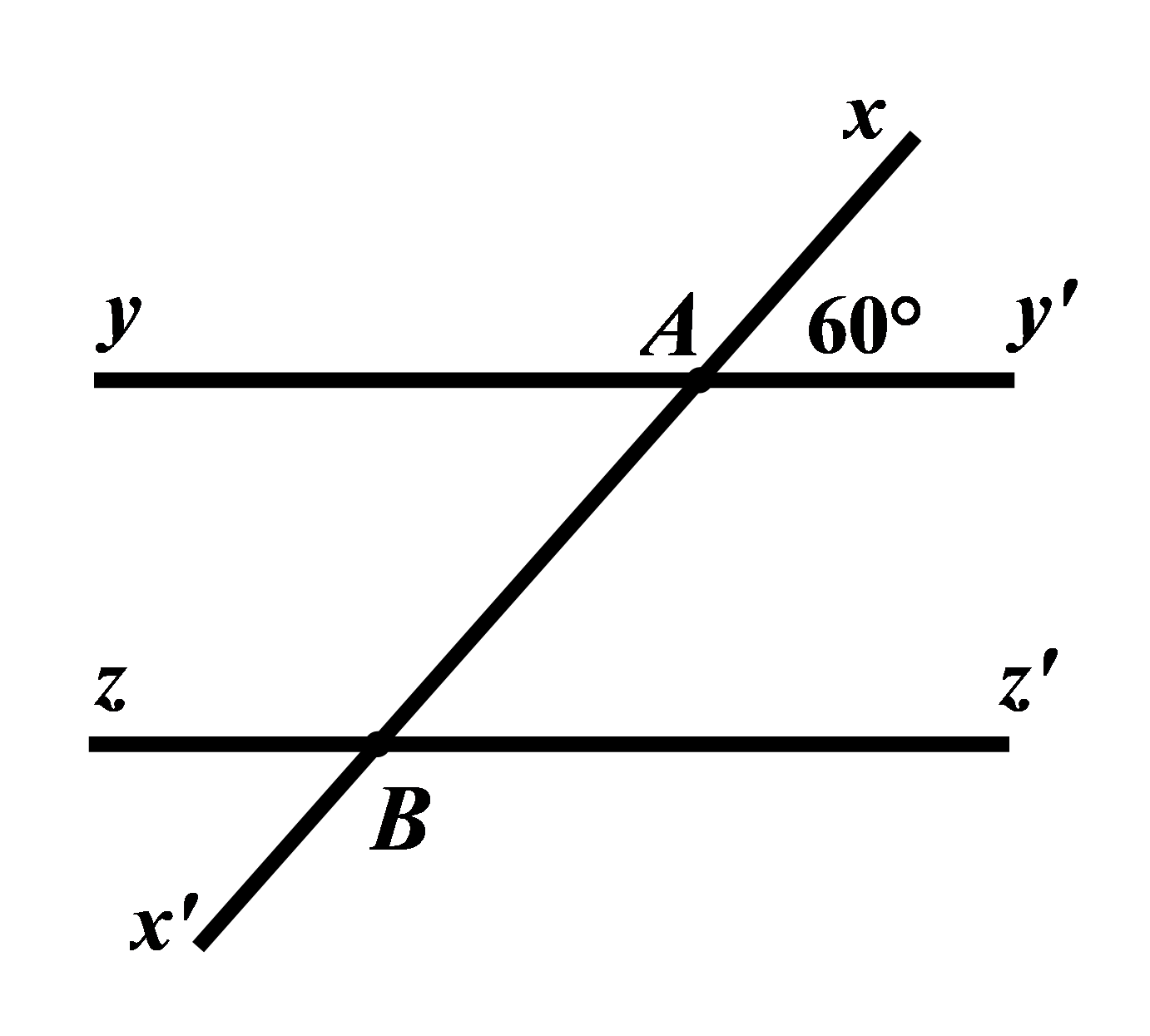
A. \(\angle zBx' = {120^0}\)
B. \(\angle zBx' = {80^0}\)
C. \(\angle zBx' = {50^0}\)
D. \(\angle zBx' = {60^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\left( {2\frac{5}{6} + 1\frac{4}{9}} \right):\left( {10\frac{1}{{12}} - 9,5} \right)\)
b) \(\frac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\frac{{25}}{{16}}} \)
d) \(\left| {\frac{1}{{ - 5}}} \right| - \frac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \frac{{\left| 2 \right|}}{5}\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(x - \frac{1}{2} = 3\frac{1}{2}:\frac{7}{2}\)
b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
c) \(\sqrt {1,96} + 3\frac{x}{4} = \sqrt {0,04} + \frac{1}{4}.\sqrt {{{\left( {\frac{{89}}{5}} \right)}^2}} \)
d) \(\left| {2x:\frac{4}{5} - \frac{{1,6}}{4}} \right| = \frac{7}{5}\)
Bài 3: (1,5 điểm)
Ba lớp 7A, 7B, 7C được phân công đi lao động với khối lượng công việc như nhau. Lớp 7A, 7B, 7C lần lượt hoàn thành công việc trong 3 giờ, 4 giờ, 5 giờ. Tính số học sinh của mỗi lớp, biết rằng tổng số học sinh của ba lớp là 94 học sinh. Giả sử năng suất lap động của mỗi học sinh là như nhau.
Bài 4: (1,0 điểm)
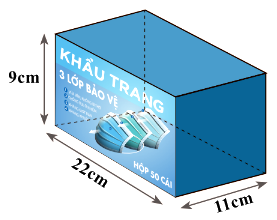
Một hộp đựng khẩu trang y tế được làm bằng bìa có dạng một hình hộp chữ nhật , kích thước như hình vẽ bên dưới.
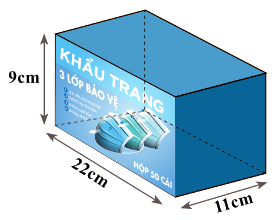
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).
Bài 5: (0,5 điểm)
Cho các số \(a,b,c\) thỏa mãn \(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}}\). Chứng tỏ rằng: \(4\left( {a - b} \right)\left( {b - c} \right) = {\left( {c - a} \right)^2}\).
Tải về
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Chọn phương án đúng?
A. \(\frac{1}{2} \notin \mathbb{Q}\)
B. \(\frac{{ - 8}}{0} \in \mathbb{Q}\)
C. \(5 \notin \mathbb{Q}\)
D. \(\frac{4}{{ - 5}} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\) là:
A. \({\left( {0,3} \right)^4}\)
B. \({\left( {0,3} \right)^{10}}\)
C. \({\left( {0,3} \right)^{15}}\)
D. \({\left( {0,3} \right)^{12}}\)
Câu 3: Sắp xếp các số sau theo thứ tự tăng dần: \(2\frac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
A. \(2\frac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
B. \(\sqrt {16} \,\,;\,\,2\frac{1}{4}\,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,\,\, - \sqrt {83} \,\,;\, - \left| { - \sqrt {196} } \right|\,.\)
C. \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\frac{1}{4}\,\,;\,\,\sqrt {16} .\)
D. \(\sqrt {16} \,\,;\,\,2\frac{1}{4}\,\,;\,\,\, - 0,0\left( {51} \right)\,\,;\,\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,.\)
Câu 4: Tìm hai số \(x;y\) biết: \(\frac{x}{4} = \frac{y}{{ - 7}}\) và \(x - y = 33\).
A. \(x = 10;y = - 23\)
B. \(x = 24;y = - 9\)
C. \(x = 15;y = - 18\)
D. \(x = 12;y = - 21\)
Câu 5: Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\), ta có thể suy ra được tỉ lệ nào trong các đáp án sau:
A. \(\frac{a}{c} = \frac{d}{b}\)
B. \(\frac{a}{b} = \frac{c}{d} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}}\)
C. \(\frac{{a + 2c}}{{b + 2d}} = \frac{{2a - c}}{{2b - d}}\)
D. \(\frac{{a + 5}}{{b + 5}} = \frac{{c + 5}}{{d + 5}}\)
Câu 6: An và Bình cùng nhau nuôi gà, An nuôi 10 con, Bình nuôi 8 con. Sau khi bán hết số gà thu được tổng cộng 3,6 triệu đồng, hai bạn quyết định số tiền tỉ lệ với số con gà mỗi bạn đã nuôi. Tính số tiền mỗi bạn nhận được.
A. An nhận được 2 triệu đồng và Bình nhận được 1,6 triệu đồng.
B. An nhận được 1,6 triệu đồng và Bình nhận được 2 triệu đồng.
C. An nhận được 2,4 triệu đồng và Bình nhận được 1,2 triệu đồng.
D. An nhận được 1,2 triệu đồng và Bình nhận được 2,4 triệu đồng.
Câu 7: Bạn Lan làm một con xúc xắc hình lập phương từ tấm bìa có kích thước như hình vẽ bên dưới.
Diện tích tấm bìa tạo thành con xúc xắc đó là bao nhiêu?
A. \(100c{m^2}\)
B. \(125c{m^2}\)
C. \(136c{m^2}\)
D. \(150c{m^2}\)
Câu 8: Gàu xúc của một xe xúc (Hình a) có dạng gần như một hình lăng trụ đứng tam giác với các kích thước đã cho ở hình b). Để xúc hết \(40{m^3}\) cát, xe phải xúc ít nhất bao nhiêu gàu?
A. \(19\)gàu
B. \(20\,\)gàu
C. \(21\) gàu
D. \(22\)gàu
Câu 9: Hai góc nào dưới đây là hai góc đối đỉnh?
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 10: Cho hình vẽ bên dưới, biết \(yy'//zz',\angle xAy' = {60^0}\). Tính số đo của \(\angle zBx'.\)
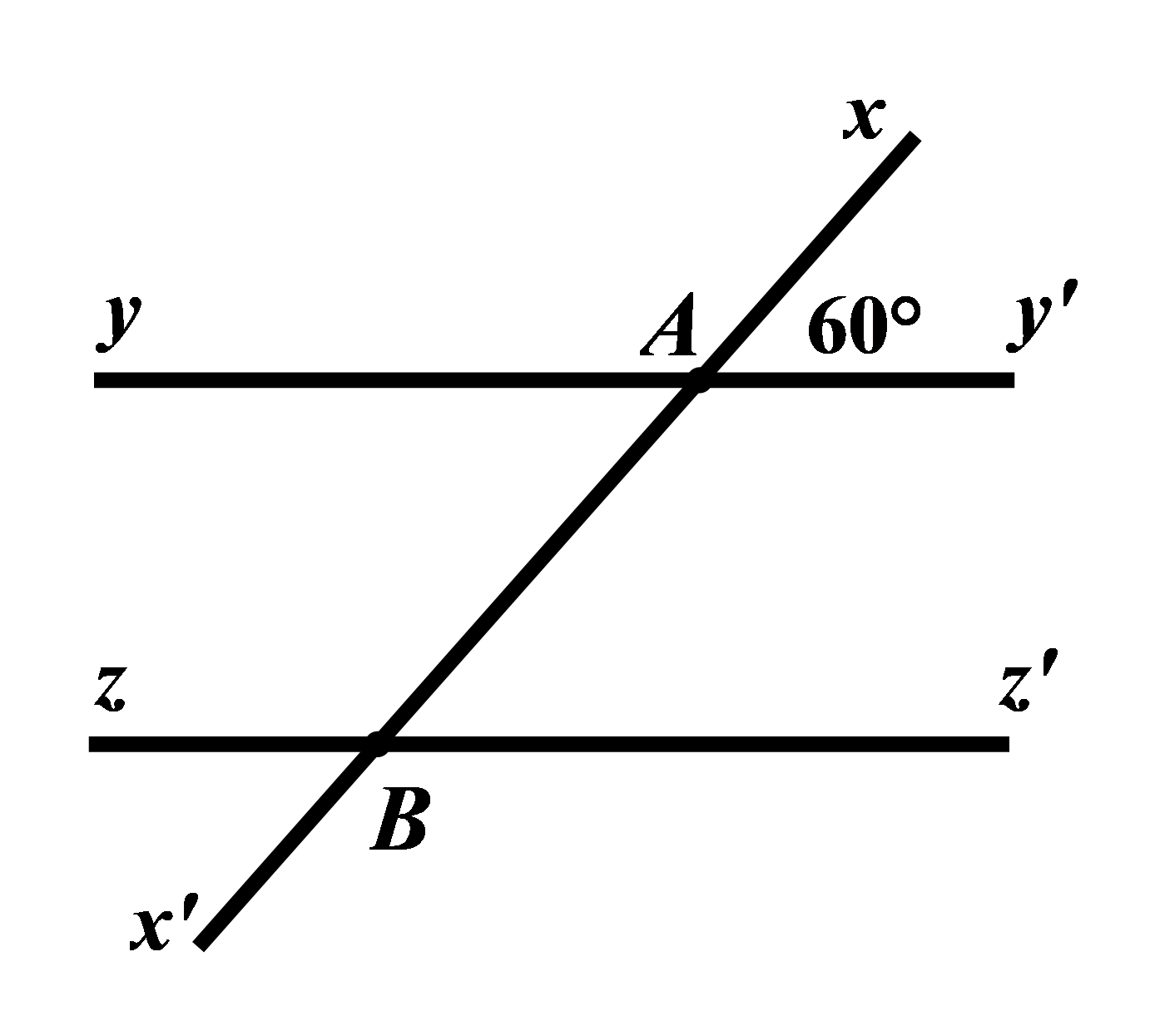
A. \(\angle zBx' = {120^0}\)
B. \(\angle zBx' = {80^0}\)
C. \(\angle zBx' = {50^0}\)
D. \(\angle zBx' = {60^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\left( {2\frac{5}{6} + 1\frac{4}{9}} \right):\left( {10\frac{1}{{12}} - 9,5} \right)\)
b) \(\frac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\frac{{25}}{{16}}} \)
d) \(\left| {\frac{1}{{ - 5}}} \right| - \frac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \frac{{\left| 2 \right|}}{5}\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(x - \frac{1}{2} = 3\frac{1}{2}:\frac{7}{2}\)
b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
c) \(\sqrt {1,96} + 3\frac{x}{4} = \sqrt {0,04} + \frac{1}{4}.\sqrt {{{\left( {\frac{{89}}{5}} \right)}^2}} \)
d) \(\left| {2x:\frac{4}{5} - \frac{{1,6}}{4}} \right| = \frac{7}{5}\)
Bài 3: (1,5 điểm)
Ba lớp 7A, 7B, 7C được phân công đi lao động với khối lượng công việc như nhau. Lớp 7A, 7B, 7C lần lượt hoàn thành công việc trong 3 giờ, 4 giờ, 5 giờ. Tính số học sinh của mỗi lớp, biết rằng tổng số học sinh của ba lớp là 94 học sinh. Giả sử năng suất lap động của mỗi học sinh là như nhau.
Bài 4: (1,0 điểm)
Một hộp đựng khẩu trang y tế được làm bằng bìa có dạng một hình hộp chữ nhật , kích thước như hình vẽ bên dưới.
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).
Bài 5: (0,5 điểm)
Cho các số \(a,b,c\) thỏa mãn \(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}}\). Chứng tỏ rằng: \(4\left( {a - b} \right)\left( {b - c} \right) = {\left( {c - a} \right)^2}\).
Phần I: Trắc nghiệm
1.D | 2.C | 3.C | 4.D | 5.C | 6.A | 7.D | 8.C | 9.C | 10.D |
Câu 1
Phương pháp:
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
Tập hợp các số hữu tỉ được kí hiệu là \(\mathbb{Q}\).
Cách giải:
Ta có:
+ \(\frac{1}{2} \in \mathbb{Q}\) nên phương án A. \(\frac{1}{2} \notin \mathbb{Q}\)là sai do đó, loại đáp án A.
+ \(\frac{{ - 8}}{0}\) không đúng với dạng số hữu tỉ (do mẫu số bằng \(0\)) nên phương án B. \(\frac{{ - 8}}{0} \in \mathbb{Q}\)là sai do đó, loại đáp án B.
+ \(5 = \frac{5}{1}\) là một số hữu tỉ và \(5 \in \mathbb{Q}\) nên phương án C. \(5 \notin \mathbb{Q}\) là sai do đó, loại đáp án C.
+ \(\frac{4}{{ - 5}}\) là một số hữu tỉ nên \(\frac{4}{{ - 5}} \in \mathbb{Q}\)do đó, phương án D đúng.
Chọn D.
Câu 2
Phương pháp:
Tính lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Tính tích của hai lũy thừa cùng cơ số: Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
Cách giải:
\({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\)\( = {\left( {0,3} \right)^{3.4}}.{\left( {0,3} \right)^3} = {\left( {0,3} \right)^{12}}.{\left( {0,3} \right)^3} = {\left( {0,3} \right)^{12 + 3}} = {\left( {0,3} \right)^{15}}\)
Chọn C.
Câu 3
Phương pháp:
Đổi hỗn số sang phân số, từ phân số đổi sang số thập phân.
Tính căn bậc hai của một số.
Tính giá trị tuyệt đối của một số.
So sánh các số để sắp xếp thứ tự tăng dần của các số.
Cách giải:
Ta có:
\(\begin{array}{l}2\frac{1}{4} = \frac{9}{4} = 2,25\\\sqrt {16} = \sqrt {{4^2}} = 4\\ - \left| { - \sqrt {196} } \right| = - \left| {\sqrt {196} } \right| = - \sqrt {196} \end{array}\)
*Vì \(2,25 < 4\) nên \(2\frac{1}{4} < \sqrt {16} \) (*)
*Vì \(83 < 196\) nên \(\sqrt {83} < \sqrt {196} \) suy ra \( - \sqrt {83} > - \sqrt {196} \) hay \( - \sqrt {83} > - \left| { - \sqrt {196} } \right|\) (1)
Vì \(0,0\left( {51} \right) < 1 = \sqrt 1 < \sqrt {83} \) suy ra \( - \sqrt {83} < - 1 < - 0,0\left( {51} \right)\) (2)
Từ (1) và (2), suy ra \( - \left| { - \sqrt {196} } \right| < - \sqrt {83} < - 0,0\left( {51} \right)\) (**)
Từ (*) và (**), suy ra \( - \left| { - \sqrt {196} } \right| < - \sqrt {83} < - 0,0\left( {51} \right) < 2\frac{1}{4} < \sqrt {16} \)
Vậy thứ tự tăng dần của các số là: \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\frac{1}{4}\,\,;\,\,\sqrt {16} .\)
Chọn C.
Câu 4
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{4} = \frac{y}{{ - 7}} = \frac{{x - y}}{{4 - \left( { - 7} \right)}} = \frac{{33}}{{11}} = 3\)
Khi đó, \(\frac{x}{4} = 3\) suy ra \(x = 4.3 = 12\)
\(\frac{y}{{ - 7}} = 3\) suy ra \(y = - 7.3 = - 21\)
Vậy \(x = 12;y = - 21\).
Chọn D.
Câu 5
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: \(\frac{a}{b} = \frac{c}{d}\) suy ra \(\frac{a}{b} = \frac{c}{d} = \frac{{2c}}{{2d}}\) hay \(\frac{a}{b} = \frac{{2c}}{{2d}} = \frac{{a + 2c}}{{b + 2d}}\) (1) (tính chất của dãy tỉ số bằng nhau)
Mặt khác, suy ra \(\frac{a}{b} = \frac{c}{d} = \frac{{2a}}{{2b}}\) hay \(\frac{a}{b} = \frac{c}{d} = \frac{{2a - c}}{{2b - d}}\) (2) (tính chất của dãy tỉ số bằng nhau)
Từ (1) và (2) suy ra \(\frac{{a + 2c}}{{b + 2d}} = \frac{{2a - c}}{{2b - d}}\)
Do đó, đáp án C đúng.
Chọn C.
Câu 6
Phương pháp:
Gọi số tiền (triệu đồng) được chia của An và Bình lần lượt là \(x\) và \(y\) (điều kiện: \(x > 0,y > 0\))
Xác định hai đại lượng tỉ lệ thuận, lập tỉ lệ thức.
Áp dụng tính chất của dãy tỉ số bằng nhau, tìm \(x\) và \(y\).
Cách giải:
Gọi số tiền (triệu đồng) được chia của An và Bình lần lượt là \(x\) và \(y\) (điều kiện: \(x > 0,y > 0\))
Do số tiền và số gà nuôi của hai bạn là hai đại lượng tỉ lệ thuận với nhau nên ta có: \(\frac{x}{{10}} = \frac{y}{8}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{10}} = \frac{y}{8} = \frac{{x + y}}{{10 + 8}} = \frac{{3,6}}{{18}} = \frac{1}{5}\)
Khi đó, \(\frac{x}{{10}} = \frac{1}{5}\) suy ra \(x = 10.\frac{1}{5} = 2\,\left( {tm} \right)\)
\(\frac{y}{8} = \frac{1}{5}\) suy ra \(y = 8.\frac{1}{5} = 1,6\,\left( {tm} \right)\)
Vậy An nhận được 2 triệu đồng và Bình nhận được 1,6 triệu đồng.
Chọn A.
Câu 7
Phương pháp:
Diện tích xung quanh của hình lập phương có một cạnh là \(a\): \({S_{xq}} = 4{a^2}\).
Diện tích hình vuông có độ dài một cạnh là \(a\): \(S = {a^2}\)
Cách giải:
Diện tích tấm bìa tạo thành con xúc xắc đó bao gồm diện tích xung quanh của hình lập phương và tổng diện tích hai mặt đáy của hình lập phương.
Vậy diện tích tấm bìa tạo thành con xúc xắc là:
\({4.5^2} + {2.5^2} = 150\,\left( {c{m^2}} \right)\)
Chọn D.
Câu 8
Phương pháp:
Thể tích của hình lăng trụ đứng tam giác: \(V = S\)đáy\(.h\)
Cách giải:
Thể tích của gàu xúc hình lăng trụ đứng tam giác là: \(V = S\)đáy\(.h = \frac{1}{2}.1.1,2.3,2 = 1,92\,\left( {{m^3}} \right)\)
Ta có: \(\frac{{40}}{{1,92}} = \frac{{125}}{6} \approx 20,8\left( 3 \right)\)
Vậy xe phải xúc ít nhất \(21\) gàu để hết \(40{m^3}\) cát.
Chọn C.
Câu 9
Phương pháp:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Cách giải:
Từ các hình vẽ, ta nhận thấy Hình 3 là hình vẽ của hai góc đối đỉnh.
Chọn C.
Câu 10
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Cách giải:
Vì \(yy'//zz'\) nên \(\angle xAy' = \angle xBz' = {60^0}\) (hai góc đồng vị)
Vì \(\angle xBz'\) và \(\angle zBx'\) là hai đối đỉnh nên \(\angle xBz' = \angle zBx' = {60^0}\).
Vậy \(\angle zBx' = {60^0}\)
Chọn D.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
a) Đổi hỗn số sang phân số.
Thực hiện các phép toán với số hữu tỉ.
b) Tích và thương của hai lũy thừa cùng cơ số:
+ Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
+ Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\)
Lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Tính \({\left( {a.b} \right)^m} = {a^m}.{b^m}\)
c) Tính căn bậc hai số học của một số thực
Thực hiện các phép toán với số hữu tỉ.
d) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) \(\left( {2\frac{5}{6} + 1\frac{4}{9}} \right):\left( {10\frac{1}{{12}} - 9,5} \right)\)
\(\begin{array}{l} = \left( {\frac{{17}}{6} + \frac{{13}}{9}} \right):\left( {\frac{{121}}{{12}} - \frac{{19}}{2}} \right)\\ = \left( {\frac{{51}}{{18}} + \frac{{26}}{{18}}} \right):\left( {\frac{{121}}{{12}} - \frac{{114}}{{12}}} \right)\\ = \frac{{77}}{{18}}:\frac{7}{{12}} = \frac{{77}}{{18}}.\frac{{12}}{7}\\ = \frac{{22}}{3}\end{array}\)
b) \(\frac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
\(\begin{array}{l} = \frac{{{{\left( {{2^5}} \right)}^3}.{{\left( {{3^2}} \right)}^5}}}{{{{\left( {{2^3}} \right)}^3}.{{\left( {2.3} \right)}^6}}} = \frac{{{2^{5.3}}{{.3}^{2.5}}}}{{{2^{3.3}}{{.2}^6}{{.3}^6}}}\\ = \frac{{{2^{15}}{{.3}^{10}}}}{{{2^9}{{.2}^6}{{.3}^6}}} = \frac{{{2^{15}}{{.3}^{10}}}}{{{2^{9 + 6}}{{.3}^6}}}\\ = \frac{{{2^{15}}{{.3}^{10}}}}{{{2^{15}}{{.3}^6}}} = \frac{{{3^{10}}}}{{{3^6}}}\\ = {3^{10 - 6}} = {3^4} = 81\end{array}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\frac{{25}}{{16}}} \)
\(\begin{array}{l} = \sqrt {{8^2}} + 2.\sqrt {{3^2}} - 8.\sqrt {{{\left( {\frac{5}{4}} \right)}^2}} \\ = 8 + 2.3 - 8.\frac{5}{4}\\ = 8 + 6 - 10\\ = 4\end{array}\)
d) \(\left| {\frac{1}{{ - 5}}} \right| - \frac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \frac{{\left| 2 \right|}}{5}\)
\(\begin{array}{l} = \frac{1}{5} - \frac{4}{5} - \frac{2}{5}\\ = \frac{{ - 5}}{5} = - 1\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
b) Biến đổi về dạng \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\)
c) Tính căn bậc hai số học của số thực
Đổi hỗn số sang phân số
Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(x - \frac{1}{2} = 3\frac{1}{2}:\frac{7}{2}\)
\(\begin{array}{l}x - \frac{1}{2} = \frac{7}{2}:\frac{7}{2}\\x - \frac{1}{2} = \frac{7}{2}.\frac{2}{7} = 1\\x = 1 + \frac{1}{2} = \frac{2}{2} + \frac{1}{2}\\x = \frac{3}{2}\end{array}\)
Vậy \(x = \frac{3}{2}\)
b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
\(\begin{array}{l}{3^{ - 1 + x}} + {5.3^{x - 1}} = 162\\{3^{x - 1}}.\left( {1 + 5} \right) = 162\\{3^{x - 1}}.6 = 162\\{3^{x - 1}} = 162:6\\{3^{x - 1}} = 27\\{3^{x - 1}} = {3^3}\\ \Rightarrow x - 1 = 3\\\,\,\,\,\,\,\,x = 3 + 1\end{array}\)
\(x = 4\) (thỏa mãn \(x\) là số nguyên)
Vậy \(x = 4\)
c) \(\sqrt {1,96} + 3\frac{x}{4} = \sqrt {0,04} + \frac{1}{4}.\sqrt {{{\left( {\frac{{89}}{5}} \right)}^2}} \)
\(\begin{array}{l}\sqrt {{{\left( {1,4} \right)}^2}} + \frac{{12 + x}}{4} = \sqrt {{{\left( {0,2} \right)}^2}} + \frac{1}{4}.\frac{{89}}{5}\\1,4 + \frac{{12 + x}}{4} = 0,2 + \frac{{89}}{{20}}\\\frac{{12 + x}}{4} = 0,2 + \frac{{89}}{{20}} - 1,4\\\frac{{12 + x}}{4} = \frac{4}{{20}} + \frac{{89}}{{20}} - \frac{{28}}{{20}}\\\frac{{12 + x}}{4} = \frac{{13}}{4}\\ \Rightarrow 12 + x = 13\\\,\,\,\,\,\,\,x = 13 - 12\\\,\,\,\,\,\,\,x = 1\end{array}\)
Vậy \(x = 1\)
d) \(\left| {2x:\frac{4}{5} - \frac{{1,6}}{4}} \right| = \frac{7}{5}\)
\(\left| {2x:\frac{4}{5} - \frac{2}{5}} \right| = \frac{7}{5}\)
Trường hợp 1:
\(\begin{array}{l}2x:\frac{4}{5} - \frac{2}{5} = \frac{7}{5}\\2x:\frac{4}{5} = \frac{7}{5} + \frac{2}{5}\\2x:\frac{4}{5} = \frac{9}{5}\\2x = \frac{9}{5}.\frac{4}{5} = \frac{{36}}{{25}}\\x = \frac{{36}}{{25}}:2 = \frac{{36}}{{25}}.\frac{1}{2}\\x = \frac{{18}}{{25}}\end{array}\)
Vậy \(x \in \left\{ {\frac{{18}}{{25}};\frac{{ - 2}}{5}} \right\}\)
Trường hợp 2:
\(\begin{array}{l}2x:\frac{4}{5} - \frac{2}{5} = \frac{{ - 7}}{5}\\2x:\frac{4}{5} = \frac{{ - 7}}{5} + \frac{2}{5}\\2x:\frac{4}{5} = \frac{{ - 5}}{5} = - 1\\2x = - 1.\frac{4}{5} = \frac{{ - 4}}{5}\\x = \frac{{ - 4}}{5}:2 = \frac{{ - 4}}{5}.\frac{1}{2}\\x = \frac{{ - 2}}{5}\end{array}\)
Bài 3
Phương pháp:
Gọi số học sinh của lớp 7A, 7B, 7C lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Xác định hai đại lượng tỉ lệ nghịch, lập tỉ lệ thức.
Áp dụng tính chất của dãy tỉ số bằng nhau, tìm \(x,y,z\).
Cách giải:
Gọi số học sinh của lớp 7A, 7B, 7C lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Do với khối lượng công việc như nhau thì số học sinh và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên \(3x = 4y = 5z\) suy ra \(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{4}}} = \frac{z}{{\frac{1}{5}}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{4}}} = \frac{z}{{\frac{1}{5}}} = \frac{{x + y + z}}{{\frac{1}{3} + \frac{1}{4} + \frac{1}{5}}} = \frac{{94}}{{\frac{{47}}{{60}}}} = 120\)
Do đó, \(\frac{x}{{\frac{1}{3}}} = 120\) suy ra \(x = \frac{1}{3}.120 = 40\,\) (tm \(x \in {\mathbb{N}^*}\))
\(\frac{y}{{\frac{1}{4}}} = 120\) suy ra \(x = \frac{1}{4}.120 = 30\) (tm \(y \in {\mathbb{N}^*}\))
\(\frac{z}{{\frac{1}{5}}} = 120\) suy ra \(z = \frac{1}{5}.120 = 24\) (tm \(z \in {\mathbb{N}^*}\))
Vậy số học sinh của lớp 7A, 7B, 7C lần lượt là 40 học sinh, 30 học sinh, 24 học sinh.
Bài 4
Phương pháp:
a) Thể tích của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c:V = abc\)
b) Diện tích bìa cứng dùng để là hộp bao gồm diện tích xung quanh và tổng diện tích hai đáy của hộp.
Diện tích xung quanh của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\): \({S_{xq}} = 2.\left( {a + b} \right).c\)
Diện tích hình chữ nhật có chiều dài là \(a\), chiều rộng đáy là \(b\): \(S = ab\)
Cách giải:
a) Thể tích của hộp là: \(22.11.9 = 2178\,\left( {c{m^3}} \right)\)
b) Diện tích bìa cứng dùng để là hộp bao gồm diện tích xung quanh và tổng diện tích hai đáy của hộp.
Diện tích xung quanh của hộp là: \({S_{xq}} = 2.\left( {22 + 11} \right).9 = 594\,\left( {c{m^2}} \right)\)
Diện tích hai đáy của hộp là: \(S = 2.22.11 = 484\,\left( {c{m^2}} \right)\)
Diện tích bìa cứng dùng để làm hộp là: \({S_{xq}} + S = 594 + 484 = 1078\,\left( {c{m^2}} \right)\)
Bài 5
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}} = \frac{{a - b}}{{2020 - 2021}} = \frac{{b - c}}{{2021 - 2022}} = \frac{{c - a}}{{2022 - 2020}}\)
Suy ra \(\frac{{a - b}}{{ - 1}} = \frac{{b - c}}{{ - 1}} = \frac{{c - a}}{2}\) hay \(c - a = - 2\left( {a - b} \right) = - 2\left( {b - c} \right)\)
Do đó, \(\left( {c - a} \right).\left( {c - a} \right) = \left[ { - 2\left( {a - b} \right)} \right].\left[ { - 2\left( {b - c} \right)} \right]\)
Suy ra \({\left( {c - a} \right)^2} = 4\left( {a - b} \right)\left( {b - c} \right)\) (đpcm)
Đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều là một bài kiểm tra quan trọng đánh giá kiến thức và kỹ năng của học sinh sau một học kỳ học tập. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Đề thi thường được chia thành các phần sau:
Phần trắc nghiệm thường bao gồm các câu hỏi về:
Phần tự luận thường bao gồm các bài toán sau:
Để giải tốt đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều, học sinh cần:
Luyện tập với đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều mang lại nhiều lợi ích cho học sinh:
Ngoài đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau:
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 7, học sinh nên:
Đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều là một công cụ hữu ích giúp học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi. Chúc các em học sinh đạt kết quả cao trong kỳ thi sắp tới!