Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 7 - Đề số 9 - Cánh diều, một công cụ hỗ trợ học sinh ôn luyện và làm quen với cấu trúc đề thi thực tế. Đề thi được biên soạn theo chương trình học Toán 7 Cánh diều, bao gồm các dạng bài tập khác nhau, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề.
Đề thi này không chỉ là bài kiểm tra kiến thức mà còn là cơ hội để học sinh đánh giá năng lực bản thân và xác định những điểm cần cải thiện. Hãy cùng Giaitoan.edu.vn chinh phục kỳ thi học kì 1 Toán 7 một cách tự tin nhất!
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. Phần trắc nghiệm (3 điểm)
Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Đáp án | A | C | A | C | C | B | C | D | C | A | B | A |
Câu 1
Phương pháp:
Tập hợp các số tự nhiên: N = {0;1;2;3;…}
Tập hợp các số nguyên: Z = {-3;-2;-1;0;1;2;3;….}
Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\)
Cách giải:
\(\dfrac{3}{7} \in \mathbb{Q}\) nên A đúng.
\(\dfrac{1}{2} \notin \mathbb{Z}\) nên B sai
\(\dfrac{{ - 9}}{5} \in \mathbb{Q}\) nên C sai
\( - 6 \notin \mathbb{N}\) nên D sai.
Chọn A.
Câu 2
Phương pháp:
Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\)
Cách giải:
Tập hợp các số hữu tỉ kí hiệu là Q
Chọn C.
Câu 3
Phương pháp:
Hai số đối nhau nếu chúng có tổng là 0.
Số đối của số a là số -a.
Cách giải:
Số đối của \(\dfrac{{ - 2}}{3}\) là \(\dfrac{2}{3}\)
Chọn A.
Câu 4
Phương pháp:
Xác định 1 đơn vị được chia thành bao nhiêu phần.
Các số nằm bên trái gốc O là các số âm.
Cách giải:
Điểm B nằm bên trái gốc O và cách gốc O một khoảng bằng \(\dfrac{1}{3}\) nên điểm B biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{3}\).
Chọn C.
Câu 5
Phương pháp:
Các phép tính với lũy thừa
Cách giải:
\({x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}\left( {x \ne 0} \right)\) nên A đúng
\({x^4}.{x^8} = {x^{4 + 8}} = {x^{12}}\) nên B đúng
\({x^2}.{x^6} = {x^{2 + 6}} = {x^8}\) nên C sai.
\({({x^3})^4} = {x^{3.4}} = {x^{12}}\) nên D đúng.
Chọn C.
Câu 6
Phương pháp:
Nhận biết số thập phân hữu hạn
Cách giải:
\(\dfrac{4}{6} = 0,66...6\) là số thập phân vô hạn tuần hoàn với chu kì 6.
\(\dfrac{3}{4} = 0,75\) là số thập phân hữu hạn.
\(\dfrac{{20}}{{15}} = 1,333....3\) là số thập phân vô hạn tuần hoàn với chu kì 3.
\(\dfrac{5}{4} = 1,25\) là số thập phân hữu hạn
Vậy các số thập phân hữu hạn là \(\dfrac{3}{4} = 0,75\) và \(\dfrac{5}{4} = 1,25\)
Chọn B.
Câu 7
Phương pháp:
Đặc điểm của hình hộp chữ nhật
Cách giải:
Hình hộp chữ nhật có 6 mặt.
Chọn C.
Câu 8
Phương pháp:
Thể tích hình hộp chữ nhật có kích thước a, b, c là: V = a.b.c
Cách giải:
Thể tích hình lăng trụ ABCD.A’B’C’D’ là: V = 4.2.3 = 24 (cm3).
Chọn D.
Câu 9
Phương pháp:
Diện tích xung quanh của hình hộp chữ nhật có chiều rộng a, chiều dài b, chiều cao c là: Sxq = 2.(a+b).c
Cách giải:
Diện tích xung quanh hình hộp chữ nhật là: Sxq = 2.(2+4).3 = 36 (cm2).
Chọn C.
Câu 10
Phương pháp:
Tiên đề Euclid.
Cách giải:
Qua một điểm M nằm ngoài đường thẳng a, có duy nhất một đường thẳng đi qua M và song song với a.
Chọn A.
Câu 11
Phương pháp:
Vận dụng định nghĩa về đại lượng tỉ lệ nghịch.
Cách giải:
Ta có: \(x = \dfrac{5}{y}\) là hai đại lượng tỉ lệ nghịch với nhau.
Chọn B.
Câu 12
Phương pháp:
Nếu Om là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOm} = \widehat {yOm} = \dfrac{1}{2}.\widehat {xOy}\)
Cách giải:
Vì Oy là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOy} = \widehat {yOz} = {20^\circ }\)
Chọn A.
II. Phần tự luận (7 điểm)
Câu 1
Phương pháp:
Thực hiện phép tính theo thứ tự thực hiện phép tính.
Tính căn bậc hai số học của một số.
Cách giải:
a) \(\sqrt 9 - \dfrac{2}{3} = 3 - \dfrac{2}{3} = \dfrac{9}{3} - \dfrac{2}{3} = \dfrac{7}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0} = - 5 + 5 + 1 = 1\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2 = {\left[ {{{\left( {\dfrac{1}{2}} \right)}^2}} \right]^2}.{\left( {\dfrac{1}{2}} \right)^5}.\dfrac{1}{2} = {\left( {\dfrac{1}{2}} \right)^4}.{\left( {\dfrac{1}{2}} \right)^5}.{\left( {\dfrac{1}{2}} \right)^1} = {\left( {\dfrac{1}{2}} \right)^{4 + 5 + 1}} = {\left( {\dfrac{1}{2}} \right)^{10}}\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3} = \dfrac{{25}}{{10}} + \dfrac{2}{3} - \dfrac{{10}}{3} = \dfrac{5}{2} - \dfrac{8}{3} = \dfrac{{15}}{6} - \dfrac{{16}}{6} = \dfrac{{ - 1}}{6}\)
Câu 2
Phương pháp:
\(\left| x \right| = a{\mkern 1mu} \) với \((a > 0)\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = a}\\{x = - a}\end{array}} \right.\)
Cách giải:
a)
\(\begin{array}{*{20}{l}}{2x - 3,7 = 10}\\{2x = 10 + 3,7}\\{2x = 13,7}\\{x = 13,7:2}\\{x = 6,85.}\end{array}\)
Vậy x = 6,85.
b)
\(\begin{array}{*{20}{l}}{\sqrt {49} + 5x - 1 = {{\left( { - 2} \right)}^3}}\\{7 + 5x - 1 = - 8}\\{5x = - 8 - 7 + 1}\\{5x = - 14}\\{x = \dfrac{{ - 14}}{5}}\end{array}\)
Vậy \(x = \dfrac{{ - 14}}{5}\)
c)
\(\begin{array}{*{20}{l}}{\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}}\\{ \Leftrightarrow \dfrac{8}{3}.|2x + 1| = \dfrac{{10}}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}:\dfrac{8}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}.\dfrac{3}{8}}\\{ \Leftrightarrow |2x + 1| = \dfrac{5}{4}}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x + 1 = \dfrac{5}{4}}\\{2x + 1 = \dfrac{{ - 5}}{4}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \dfrac{1}{4}}\\{2x = \dfrac{{ - 3}}{2}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{1}{8}}\\{x = \dfrac{{ - 3}}{4}}\end{array}} \right.}\end{array}\)
Vậy \(x \in \left\{ {\dfrac{1}{8};\dfrac{{ - 3}}{4}} \right\}\)
Câu 3
Phương pháp:
Gọi chiều dài của 3 tấm vải lúc đầu lần lượt là \(a,b,c\,\left( m \right)\) (điều kiện: \(a,b,c > 0\))
Tính chiều dài còn lại của tấm vải thứ nhất, thứ hai và thứ 3 sau khi bán.
Lập tỉ lệ thức, áp dụng tính chất của dãy tỉ số bằng nhau, tìm được chiều dài mỗi tâm vải lúc đầu.
Cách giải:
Gọi chiều dài của 3 tấm vải lúc đầu lần lượt là \(a,b,c\,\left( m \right)\) (điều kiện: \(a,b,c > 0\))
Sau khi bán \(\dfrac{1}{2}\) tấm thì chiều dài tấm vải thứ nhất là: \(\dfrac{a}{2}\,\left( m \right)\)
Sau khi bán \(\dfrac{2}{3}\) tấm thì chiều dài tấm vải thứ hai là: \(\dfrac{b}{3}\,\left( m \right)\)
Sau khi bán \(\dfrac{3}{4}\) tấm thì chiều dài tấm vải thứ ba là: \(\dfrac{c}{4}\,\left( m \right)\)
Theo đề bài ta có: \(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4}\) và \(a + b + c = 126\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4} = \dfrac{{a + b + c}}{{2 + 3 + 4}} = \dfrac{{126}}{9} = 14\)
Từ đó suy ra:
\(\dfrac{a}{2} = 14 \Rightarrow a = 14.2 = 28\,\) (thỏa mãn \(a > 0\))
\(\dfrac{b}{3} = 14 \Rightarrow b = 14.3 = 42\) (thỏa mãn \(b > 0\))
\(\dfrac{c}{4} = 14 \Rightarrow c = 14.4 = 56\) (thỏa mãn \(c > 0\))
Vậy chiều dài các tấm vải lần lượt là \(28\,m,\,42m,\,56m\).
Câu 4
Phương pháp:
Tính chất hai đường thẳng song song: Nếu một đường thẳng cắt đường thẳng song song thì: các góc ở vị trí so le trong bằng nhau, các góc ở vị trí đồng vị bằng nhau, các góc trong cùng phía bù nhau.
Tính chất các góc kề bù, các góc đối đỉnh.
Cách giải:
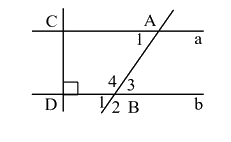
a) Vì \(a//b,b \bot CD \Rightarrow a \bot CD\)
b) Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_3}}\) (2 góc so le trong), mà \(\widehat {{A_1}} = {65^\circ } \Rightarrow \widehat {{B_3}} = {65^\circ }\)
Ta có: \(\widehat {{B_3}} = \widehat {{B_1}}\) (2 góc đối đỉnh) nên \(\widehat {{B_1}} = {65^\circ }\).
Vì \(\widehat {{B_3}} + \widehat {{B_4}} = {180^\circ }\) (2 góc kề bù) nên \({65^\circ } + \widehat {{B_4}} = {180^\circ } \Leftrightarrow \widehat {{B_4}} = {180^\circ } - {65^\circ } = {115^\circ }\).
Mà \(\widehat {{B_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh) nên \(\widehat {{B_2}} = {115^\circ }\).
Vậy \(\widehat {{B_1}} = \widehat {{B_3}} = {65^\circ }\); \(\widehat {{B_2}} = \widehat {{B_4}} = {115^\circ }\).
Câu 5
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\) nên \(\dfrac{a}{b} = \dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}} = \dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}\)
Mà \(\dfrac{a}{b} = \dfrac{{2019b}}{{2020c}}\) và \(\dfrac{a}{b} = \dfrac{b}{c}\) (gt) nên \({\left( {\dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}} \right)^3} = {\left( {\dfrac{a}{b}} \right)^3} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{a}{b} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{b}{c} = \dfrac{{{a^2}}}{{bc}}\) (đpcm)
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Trong các câu sau câu nào đúng?
A.\(\dfrac{3}{7} \in \mathbb{Q}\)
B. \(\dfrac{1}{2} \in \mathbb{Z}\).
C. \(\dfrac{{ - 9}}{5} \notin \mathbb{Q}\).
D. \( - 6 \in \mathbb{N}\).
Câu 2:Tập hợp các số hữu tỉ kí hiệu là:
A.N;
B. \({N^*}\);
C. Q;
D. Z.
Câu 3: Số đối cùa \(\dfrac{{ - 2}}{3}\) là:
A. \(\dfrac{2}{3}\);
B. \(\dfrac{3}{2}\);
C. \(\dfrac{{ - 3}}{2}\);
D. \(\dfrac{2}{{ - 3}}\).
Câu 4: Điểm B trên trục số biểu diễn số hữu tỉ nào sau đây?

A. \(\dfrac{{ - 2}}{3}\);
B. \(\dfrac{{ - 2}}{5}\);
C. \( - \dfrac{1}{3}\);
D. \(\dfrac{2}{6}\).
Câu 5: Phép tính nào sau đây không đúng?
A. \({x^{18}}:{x^6} = {x^{12}}\left( {x \ne 0} \right)\)
B. \({x^4}.{x^8} = {x^{12}}\)
C.\({x^2}.{x^6} = {x^{12}}\)
D. \({({x^3})^4} = {x^{12}}\)
Câu 6: Cho các số sau \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3;\dfrac{5}{4} = 1,25\) số nào viết được dưới dạng số thập phân hữu hạn?
A.\(\dfrac{4}{6} = 0,66...6;\dfrac{{20}}{{15}} = 1,333....3\);
B. \(\dfrac{3}{4} = 0,75;\dfrac{5}{4} = 1,25\);
C. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75\);
D. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3\).
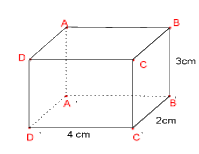
Câu 7: Số mặt của hình hộp chữ nhật \(ABCD{A^,}{B^,}{C^,}{D^,}\) là:
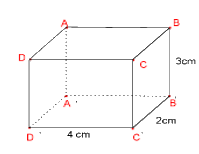
A. 3;
B. 4;
C. 6;
D. 12.
Câu 8: Thể tích của hình hộp chữ nhật bên là:
A.6 cm3;
B. 8 cm3;
C. 12 cm3;
D. 24 cm3.
Câu 9:Diện tích xung quanh của hình hộp chữ nhật bên là:
A. 12 cm2;
B. 24 cm2;
C. 36 cm2;
D. 42 cm2
Câu 10: Tiên đề Euclid được phát biểu: “Qua một điểm M nằm ngoài đường thẳng a.”
A.Có duy nhất một đường thẳng đi qua M và song song với a.
B.Có hai đường thẳng song song với a.
C.Có ít nhất một đường thẳng song song với a.
D.Có vô số đường thẳng song song với a.
Câu 11: Hai đại lượng \(x,y\) trong công thức nào tỉ lệ nghịch với nhau:
A. \(y = 5 + x\)
B. \(x = \dfrac{5}{y}\)
C. \(y = 5x\)
D. \(x = 5y\)
Câu 12: Cho hình vẽ, biết\(\widehat {\;xOy} = {20^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\).
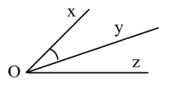
Khi đó số đo \(\widehat {yOz\;}\)bằng:
A. \({20^0}\)
B. \(\;{160^0}\)
C. \({80^0}\)
D. \(\;{40^0}\).
II. TỰ LUẬN (7 điểm)
Câu 1:(2 điểm) Tính:
a) \(\sqrt 9 - \dfrac{2}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0}\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3}\)
Câu 2: (1,5 điểm) Tìm x:
a) \(2x - 3,7 = 10\)
b) \(\sqrt {49} + 5x - 1 = {\left( { - 2} \right)^3}\)
c) \(\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}\)
Câu 3: (1,5 điểm)
Cửa hàng có 3 tấm vải dài tổng cộng \(126m\). Sau khi bán đi \(\dfrac{1}{2}\) tấm vải thứ nhất, \(\dfrac{2}{3}\) tấm vải thứ hai; \(\dfrac{3}{4}\) tấm vải thứ ba thì số vải còn lại ở cả 3 tấm bằng nhau. Tính chiều dài mỗi tấm vải lúc đầu.
Câu 4: (1,5 điểm) Cho hình vẽ sau. Biết a // b.
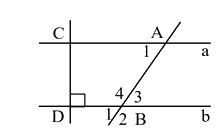
a) Chứng minh CD vuông góc với a.
b) Biết số đo góc A1 là 65o. Tính số đo góc B1 ; B2 ; B3 ; B4.
Câu 5:(0,5 điểm) Cho các số thực \(a,b,c,d,e\) thỏa mãn: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\).
Chứng minh rằng: \({\left( {\dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}} \right)^3} = \dfrac{{{a^2}}}{{bc}}\).
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Trong các câu sau câu nào đúng?
A.\(\dfrac{3}{7} \in \mathbb{Q}\)
B. \(\dfrac{1}{2} \in \mathbb{Z}\).
C. \(\dfrac{{ - 9}}{5} \notin \mathbb{Q}\).
D. \( - 6 \in \mathbb{N}\).
Câu 2:Tập hợp các số hữu tỉ kí hiệu là:
A.N;
B. \({N^*}\);
C. Q;
D. Z.
Câu 3: Số đối cùa \(\dfrac{{ - 2}}{3}\) là:
A. \(\dfrac{2}{3}\);
B. \(\dfrac{3}{2}\);
C. \(\dfrac{{ - 3}}{2}\);
D. \(\dfrac{2}{{ - 3}}\).
Câu 4: Điểm B trên trục số biểu diễn số hữu tỉ nào sau đây?

A. \(\dfrac{{ - 2}}{3}\);
B. \(\dfrac{{ - 2}}{5}\);
C. \( - \dfrac{1}{3}\);
D. \(\dfrac{2}{6}\).
Câu 5: Phép tính nào sau đây không đúng?
A. \({x^{18}}:{x^6} = {x^{12}}\left( {x \ne 0} \right)\)
B. \({x^4}.{x^8} = {x^{12}}\)
C.\({x^2}.{x^6} = {x^{12}}\)
D. \({({x^3})^4} = {x^{12}}\)
Câu 6: Cho các số sau \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3;\dfrac{5}{4} = 1,25\) số nào viết được dưới dạng số thập phân hữu hạn?
A.\(\dfrac{4}{6} = 0,66...6;\dfrac{{20}}{{15}} = 1,333....3\);
B. \(\dfrac{3}{4} = 0,75;\dfrac{5}{4} = 1,25\);
C. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75\);
D. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3\).
Câu 7: Số mặt của hình hộp chữ nhật \(ABCD{A^,}{B^,}{C^,}{D^,}\) là:
A. 3;
B. 4;
C. 6;
D. 12.
Câu 8: Thể tích của hình hộp chữ nhật bên là:
A.6 cm3;
B. 8 cm3;
C. 12 cm3;
D. 24 cm3.
Câu 9:Diện tích xung quanh của hình hộp chữ nhật bên là:
A. 12 cm2;
B. 24 cm2;
C. 36 cm2;
D. 42 cm2
Câu 10: Tiên đề Euclid được phát biểu: “Qua một điểm M nằm ngoài đường thẳng a.”
A.Có duy nhất một đường thẳng đi qua M và song song với a.
B.Có hai đường thẳng song song với a.
C.Có ít nhất một đường thẳng song song với a.
D.Có vô số đường thẳng song song với a.
Câu 11: Hai đại lượng \(x,y\) trong công thức nào tỉ lệ nghịch với nhau:
A. \(y = 5 + x\)
B. \(x = \dfrac{5}{y}\)
C. \(y = 5x\)
D. \(x = 5y\)
Câu 12: Cho hình vẽ, biết\(\widehat {\;xOy} = {20^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\).
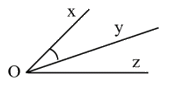
Khi đó số đo \(\widehat {yOz\;}\)bằng:
A. \({20^0}\)
B. \(\;{160^0}\)
C. \({80^0}\)
D. \(\;{40^0}\).
II. TỰ LUẬN (7 điểm)
Câu 1:(2 điểm) Tính:
a) \(\sqrt 9 - \dfrac{2}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0}\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3}\)
Câu 2: (1,5 điểm) Tìm x:
a) \(2x - 3,7 = 10\)
b) \(\sqrt {49} + 5x - 1 = {\left( { - 2} \right)^3}\)
c) \(\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}\)
Câu 3: (1,5 điểm)
Cửa hàng có 3 tấm vải dài tổng cộng \(126m\). Sau khi bán đi \(\dfrac{1}{2}\) tấm vải thứ nhất, \(\dfrac{2}{3}\) tấm vải thứ hai; \(\dfrac{3}{4}\) tấm vải thứ ba thì số vải còn lại ở cả 3 tấm bằng nhau. Tính chiều dài mỗi tấm vải lúc đầu.
Câu 4: (1,5 điểm) Cho hình vẽ sau. Biết a // b.
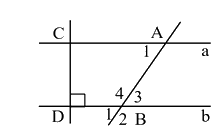
a) Chứng minh CD vuông góc với a.
b) Biết số đo góc A1 là 65o. Tính số đo góc B1 ; B2 ; B3 ; B4.
Câu 5:(0,5 điểm) Cho các số thực \(a,b,c,d,e\) thỏa mãn: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\).
Chứng minh rằng: \({\left( {\dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}} \right)^3} = \dfrac{{{a^2}}}{{bc}}\).
I. Phần trắc nghiệm (3 điểm)
Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Đáp án | A | C | A | C | C | B | C | D | C | A | B | A |
Câu 1
Phương pháp:
Tập hợp các số tự nhiên: N = {0;1;2;3;…}
Tập hợp các số nguyên: Z = {-3;-2;-1;0;1;2;3;….}
Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\)
Cách giải:
\(\dfrac{3}{7} \in \mathbb{Q}\) nên A đúng.
\(\dfrac{1}{2} \notin \mathbb{Z}\) nên B sai
\(\dfrac{{ - 9}}{5} \in \mathbb{Q}\) nên C sai
\( - 6 \notin \mathbb{N}\) nên D sai.
Chọn A.
Câu 2
Phương pháp:
Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\)
Cách giải:
Tập hợp các số hữu tỉ kí hiệu là Q
Chọn C.
Câu 3
Phương pháp:
Hai số đối nhau nếu chúng có tổng là 0.
Số đối của số a là số -a.
Cách giải:
Số đối của \(\dfrac{{ - 2}}{3}\) là \(\dfrac{2}{3}\)
Chọn A.
Câu 4
Phương pháp:
Xác định 1 đơn vị được chia thành bao nhiêu phần.
Các số nằm bên trái gốc O là các số âm.
Cách giải:
Điểm B nằm bên trái gốc O và cách gốc O một khoảng bằng \(\dfrac{1}{3}\) nên điểm B biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{3}\).
Chọn C.
Câu 5
Phương pháp:
Các phép tính với lũy thừa
Cách giải:
\({x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}\left( {x \ne 0} \right)\) nên A đúng
\({x^4}.{x^8} = {x^{4 + 8}} = {x^{12}}\) nên B đúng
\({x^2}.{x^6} = {x^{2 + 6}} = {x^8}\) nên C sai.
\({({x^3})^4} = {x^{3.4}} = {x^{12}}\) nên D đúng.
Chọn C.
Câu 6
Phương pháp:
Nhận biết số thập phân hữu hạn
Cách giải:
\(\dfrac{4}{6} = 0,66...6\) là số thập phân vô hạn tuần hoàn với chu kì 6.
\(\dfrac{3}{4} = 0,75\) là số thập phân hữu hạn.
\(\dfrac{{20}}{{15}} = 1,333....3\) là số thập phân vô hạn tuần hoàn với chu kì 3.
\(\dfrac{5}{4} = 1,25\) là số thập phân hữu hạn
Vậy các số thập phân hữu hạn là \(\dfrac{3}{4} = 0,75\) và \(\dfrac{5}{4} = 1,25\)
Chọn B.
Câu 7
Phương pháp:
Đặc điểm của hình hộp chữ nhật
Cách giải:
Hình hộp chữ nhật có 6 mặt.
Chọn C.
Câu 8
Phương pháp:
Thể tích hình hộp chữ nhật có kích thước a, b, c là: V = a.b.c
Cách giải:
Thể tích hình lăng trụ ABCD.A’B’C’D’ là: V = 4.2.3 = 24 (cm3).
Chọn D.
Câu 9
Phương pháp:
Diện tích xung quanh của hình hộp chữ nhật có chiều rộng a, chiều dài b, chiều cao c là: Sxq = 2.(a+b).c
Cách giải:
Diện tích xung quanh hình hộp chữ nhật là: Sxq = 2.(2+4).3 = 36 (cm2).
Chọn C.
Câu 10
Phương pháp:
Tiên đề Euclid.
Cách giải:
Qua một điểm M nằm ngoài đường thẳng a, có duy nhất một đường thẳng đi qua M và song song với a.
Chọn A.
Câu 11
Phương pháp:
Vận dụng định nghĩa về đại lượng tỉ lệ nghịch.
Cách giải:
Ta có: \(x = \dfrac{5}{y}\) là hai đại lượng tỉ lệ nghịch với nhau.
Chọn B.
Câu 12
Phương pháp:
Nếu Om là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOm} = \widehat {yOm} = \dfrac{1}{2}.\widehat {xOy}\)
Cách giải:
Vì Oy là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOy} = \widehat {yOz} = {20^\circ }\)
Chọn A.
II. Phần tự luận (7 điểm)
Câu 1
Phương pháp:
Thực hiện phép tính theo thứ tự thực hiện phép tính.
Tính căn bậc hai số học của một số.
Cách giải:
a) \(\sqrt 9 - \dfrac{2}{3} = 3 - \dfrac{2}{3} = \dfrac{9}{3} - \dfrac{2}{3} = \dfrac{7}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0} = - 5 + 5 + 1 = 1\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2 = {\left[ {{{\left( {\dfrac{1}{2}} \right)}^2}} \right]^2}.{\left( {\dfrac{1}{2}} \right)^5}.\dfrac{1}{2} = {\left( {\dfrac{1}{2}} \right)^4}.{\left( {\dfrac{1}{2}} \right)^5}.{\left( {\dfrac{1}{2}} \right)^1} = {\left( {\dfrac{1}{2}} \right)^{4 + 5 + 1}} = {\left( {\dfrac{1}{2}} \right)^{10}}\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3} = \dfrac{{25}}{{10}} + \dfrac{2}{3} - \dfrac{{10}}{3} = \dfrac{5}{2} - \dfrac{8}{3} = \dfrac{{15}}{6} - \dfrac{{16}}{6} = \dfrac{{ - 1}}{6}\)
Câu 2
Phương pháp:
\(\left| x \right| = a{\mkern 1mu} \) với \((a > 0)\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = a}\\{x = - a}\end{array}} \right.\)
Cách giải:
a)
\(\begin{array}{*{20}{l}}{2x - 3,7 = 10}\\{2x = 10 + 3,7}\\{2x = 13,7}\\{x = 13,7:2}\\{x = 6,85.}\end{array}\)
Vậy x = 6,85.
b)
\(\begin{array}{*{20}{l}}{\sqrt {49} + 5x - 1 = {{\left( { - 2} \right)}^3}}\\{7 + 5x - 1 = - 8}\\{5x = - 8 - 7 + 1}\\{5x = - 14}\\{x = \dfrac{{ - 14}}{5}}\end{array}\)
Vậy \(x = \dfrac{{ - 14}}{5}\)
c)
\(\begin{array}{*{20}{l}}{\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}}\\{ \Leftrightarrow \dfrac{8}{3}.|2x + 1| = \dfrac{{10}}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}:\dfrac{8}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}.\dfrac{3}{8}}\\{ \Leftrightarrow |2x + 1| = \dfrac{5}{4}}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x + 1 = \dfrac{5}{4}}\\{2x + 1 = \dfrac{{ - 5}}{4}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \dfrac{1}{4}}\\{2x = \dfrac{{ - 3}}{2}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{1}{8}}\\{x = \dfrac{{ - 3}}{4}}\end{array}} \right.}\end{array}\)
Vậy \(x \in \left\{ {\dfrac{1}{8};\dfrac{{ - 3}}{4}} \right\}\)
Câu 3
Phương pháp:
Gọi chiều dài của 3 tấm vải lúc đầu lần lượt là \(a,b,c\,\left( m \right)\) (điều kiện: \(a,b,c > 0\))
Tính chiều dài còn lại của tấm vải thứ nhất, thứ hai và thứ 3 sau khi bán.
Lập tỉ lệ thức, áp dụng tính chất của dãy tỉ số bằng nhau, tìm được chiều dài mỗi tâm vải lúc đầu.
Cách giải:
Gọi chiều dài của 3 tấm vải lúc đầu lần lượt là \(a,b,c\,\left( m \right)\) (điều kiện: \(a,b,c > 0\))
Sau khi bán \(\dfrac{1}{2}\) tấm thì chiều dài tấm vải thứ nhất là: \(\dfrac{a}{2}\,\left( m \right)\)
Sau khi bán \(\dfrac{2}{3}\) tấm thì chiều dài tấm vải thứ hai là: \(\dfrac{b}{3}\,\left( m \right)\)
Sau khi bán \(\dfrac{3}{4}\) tấm thì chiều dài tấm vải thứ ba là: \(\dfrac{c}{4}\,\left( m \right)\)
Theo đề bài ta có: \(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4}\) và \(a + b + c = 126\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4} = \dfrac{{a + b + c}}{{2 + 3 + 4}} = \dfrac{{126}}{9} = 14\)
Từ đó suy ra:
\(\dfrac{a}{2} = 14 \Rightarrow a = 14.2 = 28\,\) (thỏa mãn \(a > 0\))
\(\dfrac{b}{3} = 14 \Rightarrow b = 14.3 = 42\) (thỏa mãn \(b > 0\))
\(\dfrac{c}{4} = 14 \Rightarrow c = 14.4 = 56\) (thỏa mãn \(c > 0\))
Vậy chiều dài các tấm vải lần lượt là \(28\,m,\,42m,\,56m\).
Câu 4
Phương pháp:
Tính chất hai đường thẳng song song: Nếu một đường thẳng cắt đường thẳng song song thì: các góc ở vị trí so le trong bằng nhau, các góc ở vị trí đồng vị bằng nhau, các góc trong cùng phía bù nhau.
Tính chất các góc kề bù, các góc đối đỉnh.
Cách giải:
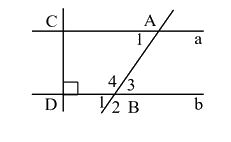
a) Vì \(a//b,b \bot CD \Rightarrow a \bot CD\)
b) Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_3}}\) (2 góc so le trong), mà \(\widehat {{A_1}} = {65^\circ } \Rightarrow \widehat {{B_3}} = {65^\circ }\)
Ta có: \(\widehat {{B_3}} = \widehat {{B_1}}\) (2 góc đối đỉnh) nên \(\widehat {{B_1}} = {65^\circ }\).
Vì \(\widehat {{B_3}} + \widehat {{B_4}} = {180^\circ }\) (2 góc kề bù) nên \({65^\circ } + \widehat {{B_4}} = {180^\circ } \Leftrightarrow \widehat {{B_4}} = {180^\circ } - {65^\circ } = {115^\circ }\).
Mà \(\widehat {{B_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh) nên \(\widehat {{B_2}} = {115^\circ }\).
Vậy \(\widehat {{B_1}} = \widehat {{B_3}} = {65^\circ }\); \(\widehat {{B_2}} = \widehat {{B_4}} = {115^\circ }\).
Câu 5
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\) nên \(\dfrac{a}{b} = \dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}} = \dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}\)
Mà \(\dfrac{a}{b} = \dfrac{{2019b}}{{2020c}}\) và \(\dfrac{a}{b} = \dfrac{b}{c}\) (gt) nên \({\left( {\dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}} \right)^3} = {\left( {\dfrac{a}{b}} \right)^3} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{a}{b} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{b}{c} = \dfrac{{{a^2}}}{{bc}}\) (đpcm)
Đề thi học kì 1 Toán 7 - Đề số 9 - Cánh diều là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau một học kỳ học tập. Đề thi này bao gồm các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Đề thi thường được chia thành các phần:
Phần này thường tập trung vào các khái niệm về số hữu tỉ, số thực, cách biểu diễn trên trục số, các phép toán trên số hữu tỉ và số thực. Học sinh cần nắm vững các tính chất của phép cộng, trừ, nhân, chia và các quy tắc dấu ngoặc.
Học sinh cần biết cách thu gọn biểu thức đại số, tìm giá trị của biểu thức tại một giá trị cụ thể của biến, và áp dụng các quy tắc biến đổi biểu thức.
Phần này yêu cầu học sinh giải phương trình bậc nhất một ẩn, kiểm tra nghiệm của phương trình, và ứng dụng phương trình để giải các bài toán thực tế.
Học sinh cần hiểu khái niệm về bất đẳng thức, các quy tắc chuyển vế, và giải bất đẳng thức bậc nhất một ẩn.
Các bài toán ứng dụng thực tế thường liên quan đến việc giải quyết các vấn đề trong đời sống, như tính toán diện tích, chu vi, vận tốc, thời gian, và các đại lượng liên quan khác.
Để giải đề thi hiệu quả, học sinh cần:
Ngoài việc làm đề thi, học sinh nên luyện tập thêm các bài tập trong sách giáo khoa, sách bài tập, và các đề thi thử khác để củng cố kiến thức và kỹ năng. Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn khi làm bài thi thực tế.
Học sinh có thể tham khảo các tài liệu sau để ôn tập:
Hãy dành thời gian ôn tập kỹ lưỡng, làm nhiều bài tập, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt trong kỳ thi học kì 1 Toán 7!
Bài toán: Giải phương trình 2x + 5 = 11
Giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 6 / 2
x = 3
Vậy nghiệm của phương trình là x = 3.
Đề thi học kì 1 Toán 7 - Đề số 9 - Cánh diều là một cơ hội tốt để học sinh đánh giá năng lực và chuẩn bị cho các kỳ thi tiếp theo. Hãy tận dụng tối đa cơ hội này để đạt kết quả tốt nhất!