Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán chương trình Cánh diều - Đề số 16.
Đề thi này được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Hãy tải đề thi về và thử sức ngay để đánh giá năng lực của bản thân nhé!
Số nào sau đây viết được dưới dạng số thập phân hữu hạn?
\(1\frac{2}{7}\).
\(\frac{1}{4}\).
\(\frac{2}{3}\).
\(\sqrt 5 \).
Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi \(x = 5\) thì \(y = 2\). Hệ số tỉ lệ là:
10.
2,5.
20.
7.
\(\sqrt {25} \) có kết quả là
-5 và 5.
-5.
5.
25.
Giá trị của \(x\) trong tỉ lệ thức \(\frac{2}{5} = \frac{8}{x}\) là:
1,25.
4.
40.
20.
Làm tròn số thập phân 5897,9391 đến hàng phần mười được kết quả là:
5898.
5897,94.
5897,9.
5897,939.
Giá trị của biểu thức \(\sqrt {0,25} - \left| { - 0,2} \right|\) là:
0,05.
0,7.
0,3.
0,45.
Cho đẳng thức 4.9 = 3.12. Tỉ lệ thức nào sau đây không đúng?
\(\frac{4}{9} = \frac{3}{{12}}\).
\(\frac{4}{{12}} = \frac{3}{9}\).
\(\frac{9}{{12}} = \frac{3}{4}\).
\(\frac{9}{3} = \frac{{12}}{4}\).
Nếu \(\frac{x}{3} = \frac{y}{4}\) và \(x + y = 21\) thì
\(x = 12;y = 9\).
\(x = 63;y = 84\).
\(x = - 9;y = - 12\).
\(x = 9;y = 12\).
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {yOz} = 55^\circ \). Số đo của \(\widehat {xOy}\) là:
\(115^\circ \).
\(125^\circ \).
\(55^\circ \).
\(180^\circ \).
Khẳng định nào dưới đây đúng?
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 4 đường chéo.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 4 đường chéo.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 6 đường chéo.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 6 đường chéo.
Cho Ot là tia phân giác của \(\widehat {xOy} = 120^\circ \). Chọn đáp án đúng:
\(\widehat {xOy} = 60^\circ \).
\(\widehat {xOt} = 120^\circ \).
\(\widehat {yOt} = 120^\circ \).
\(\widehat {xOt} = 60^\circ \).
Cho hình vẽ, biết a // b, \(\widehat {{A_1}} = 58^\circ \). Tính \(\widehat {{B_3}}\).
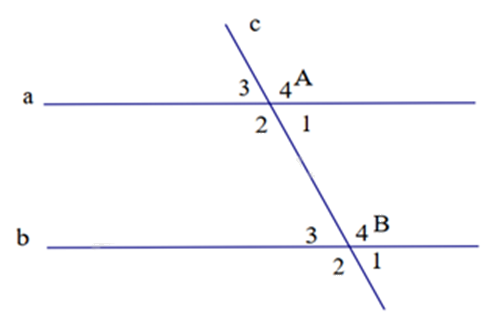
\(122^\circ \).
\(132^\circ \).
\(90^\circ \).
\(58^\circ \).
Thực hiện phép tính:
a) \(\frac{1}{2} + \frac{2}{3} - \frac{4}{5}\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{3}} \right)^7} - 2\)
c) \(\left( {1 + \frac{1}{2} + \frac{1}{3}} \right){\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\)
Tìm x, biết:
a) \(\frac{2}{5}x - \frac{1}{2} = \frac{{ - 3}}{5}\)
b) \(\left| {x - \frac{1}{2}} \right| = \frac{2}{3}\)
Môt cửa hàng văn phòng phẩm bán ba loại bút bi đỏ, đen và xanh tỉ lệ với các số 4; 6; 7. Tổng số bút bi mà cửa hàng nhập về bán là 340 chiếc. Tính số bút bi mỗi loại.
Một thùng đựng hàng bằng thép không có nắp dạng hình hộp chữ nhật có chiều dài 2m, chiều rộng 1,5m và chiều cao 2m. Người thợ cần bao nhiêu ki-lô-gam sơn để sơn bên ngoài các mặt xung quanh chiếc thùng đó? Biết rằng với mỗi ki-lô-gam sơn sẽ sơn được \(4{m^2}\) mặt thùng.
Cho hình vẽ:
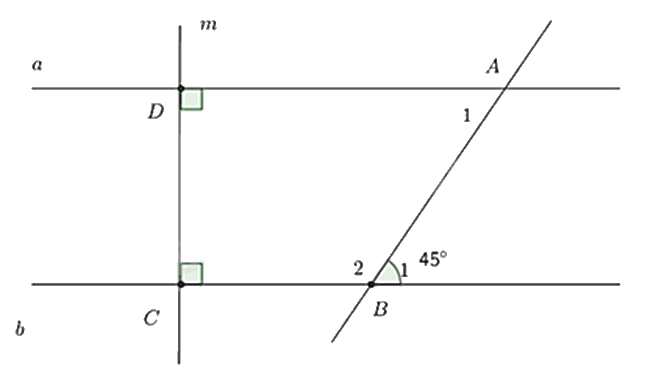
Biết \(a \bot m,b \bot m,\widehat {{B_1}} = 45^\circ \).
a) Chứng minh a // b.
b) Tính \(\widehat {{B_2}},\widehat {{A_1}}\).
c) Vẽ tia \(Dx\) là tia phân giác của \(\widehat {aDm}\), tia \(Cy\) là tia phân giác của \(\widehat {bCD}\). Chứng minh \(Dx//Cy\).
Số nào sau đây viết được dưới dạng số thập phân hữu hạn?
\(1\frac{2}{7}\).
\(\frac{1}{4}\).
\(\frac{2}{3}\).
\(\sqrt 5 \).
Đáp án : B
Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.
\(\frac{1}{4}\) có thể viết dưới dạng số thập phân hữu hạn.
\(1\frac{2}{7}\); \(\frac{2}{3}\); \(\sqrt 5 \) không viết được dưới dạng số thập phân hữu hạn.
Đáp án B
Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi \(x = 5\) thì \(y = 2\). Hệ số tỉ lệ là:
10.
2,5.
20.
7.
Đáp án : A
Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \frac{a}{x}\) hay \(xy = a\) (với a là hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Hệ số tỉ lệ của x và y là: 5.2 = 10.
Đáp án A
\(\sqrt {25} \) có kết quả là
-5 và 5.
-5.
5.
25.
Đáp án : C
\(\sqrt a = x\) với \(x \ge 0,a = {x^2}\)
\(\sqrt {25} = 5\).
Đáp án C
Giá trị của \(x\) trong tỉ lệ thức \(\frac{2}{5} = \frac{8}{x}\) là:
1,25.
4.
40.
20.
Đáp án : D
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).
Ta có: \(\frac{2}{5} = \frac{8}{x}\) nên \(2x = 5.8 = 40\) suy ra \(x = \frac{{40}}{2} = 20\).
Đáp án D
Làm tròn số thập phân 5897,9391 đến hàng phần mười được kết quả là:
5898.
5897,94.
5897,9.
5897,939.
Đáp án : C
Áp dụng quy tắc Làm tròn số thập phân dương:
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5.
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên.
Số thập phân 5897,9391 làm tròn đến hàng phần mười là: 5897,9 (vì 3 < 5).
Đáp án C
Giá trị của biểu thức \(\sqrt {0,25} - \left| { - 0,2} \right|\) là:
0,05.
0,7.
0,3.
0,45.
Đáp án : C
Sử dụng kiến thức về căn bậc hai và giá trị tuyệt đối của một số:
\(\sqrt a = x\) nếu \(x \ge 0,a = {x^2}\);
|a| = a nếu a \( \ge \) 0;
|a| = -a nếu a < 0.
\(\sqrt {0,25} - \left| { - 0,2} \right| = 0,5 - 0,2 = 0,3\).
Đáp án C
Cho đẳng thức 4.9 = 3.12. Tỉ lệ thức nào sau đây không đúng?
\(\frac{4}{9} = \frac{3}{{12}}\).
\(\frac{4}{{12}} = \frac{3}{9}\).
\(\frac{9}{{12}} = \frac{3}{4}\).
\(\frac{9}{3} = \frac{{12}}{4}\).
Đáp án : A
Nếu a.d = b.c thì \(\frac{a}{c} = \frac{b}{d};\frac{a}{b} = \frac{c}{d};\frac{c}{a} = \frac{d}{b};\frac{b}{a} = \frac{d}{c}\)
Nếu 4.9 = 3.12 thì \(\frac{4}{3} = \frac{{12}}{9};\frac{4}{{12}} = \frac{3}{9};\frac{3}{4} = \frac{9}{{12}};\frac{{12}}{4} = \frac{9}{3}\) nên A sai.
Đáp án A
Nếu \(\frac{x}{3} = \frac{y}{4}\) và \(x + y = 21\) thì
\(x = 12;y = 9\).
\(x = 63;y = 84\).
\(x = - 9;y = - 12\).
\(x = 9;y = 12\).
Đáp án : D
Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{a}{c} = \frac{b}{d} = \frac{{a + b}}{{c + d}}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3} = \frac{y}{4} = \frac{{x + y}}{{3 + 4}} = \frac{{21}}{7} = 3\)
suy ra \(x = 3.3 = 9;y = 3.4 = 12\).
Đáp án D
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {yOz} = 55^\circ \). Số đo của \(\widehat {xOy}\) là:
\(115^\circ \).
\(125^\circ \).
\(55^\circ \).
\(180^\circ \).
Đáp án : B
Hai góc kề bù thì có tổng bằng \(180^\circ \).
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \)
suy ra \(\widehat {xOy} = 180^\circ - \widehat {yOz} = 180^\circ - 55^\circ = 125^\circ \).
Đáp án B
Khẳng định nào dưới đây đúng?
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 4 đường chéo.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 4 đường chéo.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 6 đường chéo.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 6 đường chéo.
Đáp án : A
Dựa vào đặc điểm của hình hộp chữ nhật.
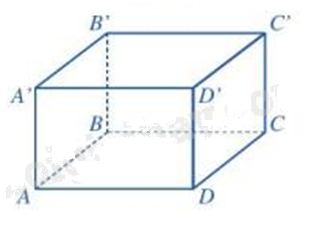
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 4 đường chéo nên đáp án A đúng.
Đáp án A
Cho Ot là tia phân giác của \(\widehat {xOy} = 120^\circ \). Chọn đáp án đúng:
\(\widehat {xOy} = 60^\circ \).
\(\widehat {xOt} = 120^\circ \).
\(\widehat {yOt} = 120^\circ \).
\(\widehat {xOt} = 60^\circ \).
Đáp án : D
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Vì Ot là tia phân giác của \(\widehat {xOy} = 120^\circ \) nên \(\widehat {xOt} = \widehat {yOt} = \frac{{120^\circ }}{2} = 60^\circ \).
Đáp án D
Cho hình vẽ, biết a // b, \(\widehat {{A_1}} = 58^\circ \). Tính \(\widehat {{B_3}}\).
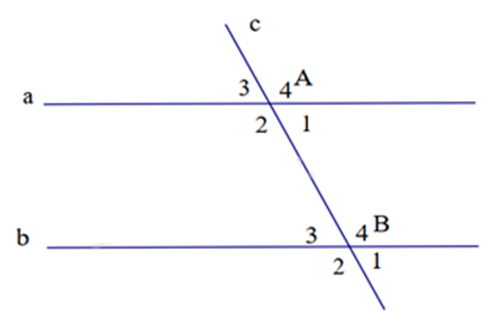
\(122^\circ \).
\(132^\circ \).
\(90^\circ \).
\(58^\circ \).
Đáp án : D
Hai đường thẳng song song thì có các góc so le trong bằng nhau, các góc đồng vị bằng nhau.
Vì a // b nên \(\widehat {{B_3}} = \widehat {{A_1}} = 58^\circ \) (hai góc so le trong)
Đáp án D
Thực hiện phép tính:
a) \(\frac{1}{2} + \frac{2}{3} - \frac{4}{5}\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{3}} \right)^7} - 2\)
c) \(\left( {1 + \frac{1}{2} + \frac{1}{3}} \right){\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\)
Áp dụng quy tắc cộng, trừ, nhân, chia với số hữu tỉ.
b) Sử dụng tính chất chia hai lũy thừa có cùng cơ số.
c) Thực hiện phép tính trong ngoặc sau đó tính lũy thừa và rút gọn.
a) \(\frac{1}{2} + \frac{2}{3} - \frac{4}{5}\)\( = \frac{{15 + 20 - 24}}{{30}} = \frac{{11}}{{30}}\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{3}} \right)^7} - 2\)\(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^{9 - 7}} - 2\)\( = \frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^2} - 2\)\( = \frac{{17}}{9} + \frac{1}{9} - 2\)\( = 2 - 2\)\( = 0\)
c) \(\left( {1 + \frac{1}{2} + \frac{1}{3}} \right){\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\)\( = \left( {\frac{{6 + 3 + 2}}{6}} \right){\left( {\frac{{16 - 15}}{{20}}} \right)^2}\)\( = \frac{{11}}{6}.{\left( {\frac{1}{{20}}} \right)^2}\)\( = \frac{{11}}{6}.\frac{1}{{400}}\)\( = \frac{{11}}{{2400}}\)
Tìm x, biết:
a) \(\frac{2}{5}x - \frac{1}{2} = \frac{{ - 3}}{5}\)
b) \(\left| {x - \frac{1}{2}} \right| = \frac{2}{3}\)
Áp dụng quy tắc chuyển vế đổi dấu.
b) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B.
a) \(\frac{2}{5}x - \frac{1}{2} = \frac{{ - 3}}{5}\)
\(\begin{array}{l}\frac{2}{5}x = \frac{{ - 3}}{5} + \frac{1}{2}\\\frac{2}{5}x = \frac{{ - 1}}{{10}}\\x = \frac{{ - 1}}{{10}}:\frac{2}{5}\\x = \frac{{ - 1}}{4}\end{array}\)
Vậy \(x = \frac{{ - 1}}{4}\).
b) \(\left| {x - \frac{1}{2}} \right| = \frac{2}{3}\)
\(x - \frac{1}{2} = \frac{2}{3}\) hoặc \(x - \frac{1}{2} = - \frac{2}{3}\)
\(x = \frac{2}{3} + \frac{1}{2}\) hoặc \(x = - \frac{2}{3} + \frac{1}{2}\)
\(x = \frac{7}{6}\) hoặc \(x = \frac{{ - 1}}{6}\)
Vậy \(x \in \left\{ {\frac{7}{6};\frac{{ - 1}}{6}} \right\}\)
Môt cửa hàng văn phòng phẩm bán ba loại bút bi đỏ, đen và xanh tỉ lệ với các số 4; 6; 7. Tổng số bút bi mà cửa hàng nhập về bán là 340 chiếc. Tính số bút bi mỗi loại.
Gọi số chiếc bút bi đỏ, đen và xanh lần lượt là: x, y, z (chiếc), \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)
Lập luận \(x + y + z = 340\)
Lập luận \(\frac{x}{4} = \frac{y}{6} = \frac{z}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.
Gọi số chiếc bút bi đỏ, đen và xanh lần lượt là: x, y, z (chiếc), \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)
Vì cửa hàng nhập về bán 340 chiếc nên \(x + y + z = 340\).
Vì số chiếc bút bi đỏ, đen và xanh tỉ lệ với các số 4; 6; 7 nên ta có: \(\frac{x}{4} = \frac{y}{6} = \frac{z}{7}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{4} = \frac{y}{6} = \frac{z}{7} = \frac{{x + y + z}}{{4 + 6 + 7}} = \frac{{340}}{{17}} = 20\)
suy ra \(x = 20.4 = 80\); \(y = 20.6 = 120\); \(z = 20.7 = 140\).
Vậy số chiếc bút bi đỏ, đen và xanh lần lượt là 80 chiếc; 120 chiếc; 140 chiếc.
Một thùng đựng hàng bằng thép không có nắp dạng hình hộp chữ nhật có chiều dài 2m, chiều rộng 1,5m và chiều cao 2m. Người thợ cần bao nhiêu ki-lô-gam sơn để sơn bên ngoài các mặt xung quanh chiếc thùng đó? Biết rằng với mỗi ki-lô-gam sơn sẽ sơn được \(4{m^2}\) mặt thùng.
Áp dụng công thức tính diện tích xung quanh của hình hộp chữ nhật để tính diện tích cần sơn chiếc thùng:
Sxq = Cđáy.chiều cao.
Số ki-lô-gam sơn = Sxq : 4.
Diện tích cần sơn là: \(2.\left( {2 + 1,5} \right).1,2 = 8,4\left( {{m^2}} \right)\)
Số ki-lô-gam sơn cần dùng là: \(8,4:4 = 2,1\left( {kg} \right)\)
Vậy người thợ cần 2,1kg sơn để sơn bên ngoài các mặt xung quanh chiếc thùng đó.
Cho hình vẽ:
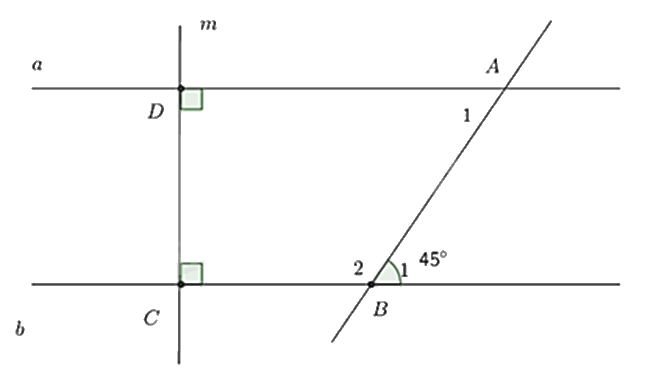
Biết \(a \bot m,b \bot m,\widehat {{B_1}} = 45^\circ \).
a) Chứng minh a // b.
b) Tính \(\widehat {{B_2}},\widehat {{A_1}}\).
c) Vẽ tia \(Dx\) là tia phân giác của \(\widehat {aDm}\), tia \(Cy\) là tia phân giác của \(\widehat {bCD}\). Chứng minh \(Dx//Cy\).
a) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau.
b) Áp dụng tính chất hai góc kề bù có tổng bằng \(180^\circ \) và hai đường thẳng song song thì hai góc so le trong bằng nhau.
c) Chứng minh hai góc ở vị trí đồng vị bằng nhau nên Dx // Cy.
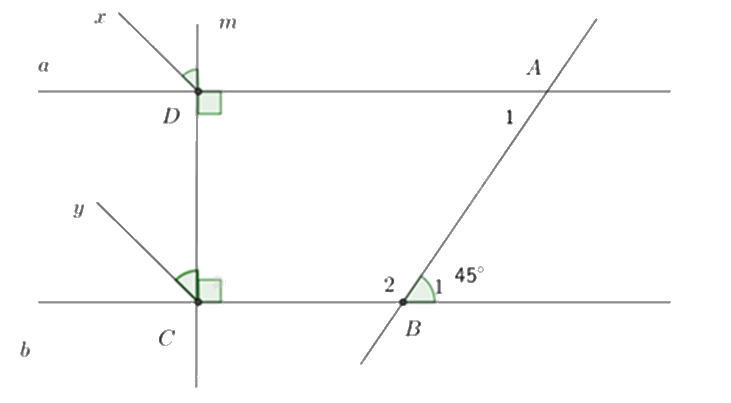
a) Ta có: \(a \bot m\) (gt), \(b \bot m\) (gt) nên a // b.
b) Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù)
\(45^\circ + \widehat {{B_2}} = 180^\circ \) suy ra \(\widehat {{B_2}} = 180^\circ - 45^\circ = 135^\circ \).
Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (hai góc so le trong)
Mà \(\widehat {{B_1}} = 45^\circ \) nên \(\widehat {{A_1}} = 45^\circ \).
c) Vì Dx là tia phân giác của \(\widehat {aDm}\) (gt) nên \(\widehat {xDm} = 90^\circ :2 = 45^\circ \)
Vì \(Cy\) là tia phân giác của \(\widehat {bCD}\) (gt) nên \(\widehat {yCD} = 90^\circ :2 = 45^\circ \)
Do đó \(\widehat {xDm} = \widehat {yCD}\)
Mà hai góc này ở vị trí đồng vị nên Dx // Cy.
Đề thi học kì 1 Toán 7 Cánh diều - Đề số 16 là một trong những đề thi quan trọng giúp học sinh lớp 7 đánh giá kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Thông thường, đề thi học kì 1 Toán 7 Cánh diều - Đề số 16 có cấu trúc gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi học kì 1 Toán 7 Cánh diều - Đề số 16:
Các bài tập về số hữu tỉ và số thực thường yêu cầu học sinh:
Các bài tập về biểu thức đại số thường yêu cầu học sinh:
Các bài tập về phương trình bậc nhất một ẩn thường yêu cầu học sinh:
Các bài tập về bất đẳng thức thường yêu cầu học sinh:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
Kết luận: Phương trình có nghiệm x = 2
Ví dụ 2: Tìm tập nghiệm của bất đẳng thức 3x - 5 < 10
Lời giải:
Kết luận: Tập nghiệm của bất đẳng thức là x < 5
Để chuẩn bị tốt nhất cho kỳ thi học kì 1 Toán 7 Cánh diều, các em có thể tham khảo các tài liệu sau:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao!