Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều, một công cụ ôn tập hiệu quả dành cho học sinh lớp 7. Đề thi được biên soạn theo chương trình Cánh diều, bao gồm các dạng bài tập khác nhau, giúp học sinh rèn luyện kỹ năng giải toán và củng cố kiến thức đã học.
Đề thi này không chỉ là bài kiểm tra kiến thức mà còn là cơ hội để học sinh tự đánh giá năng lực và xác định những phần còn yếu để tập trung ôn luyện.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 : Kết quả phép tính \(\dfrac{{ - 5}}{{12}} + \dfrac{{ - 1}}{4}\) bằng
A. \(\dfrac{{ - 1}}{2}\)
B. \(\dfrac{{ - 2}}{3}\)
C. \(\dfrac{1}{2}\)
D. \(\dfrac{2}{3}\)
Câu 2 : Giá trị của x thỏa mãn đẳng thức \({x^3} = {\rm{\;}} - 27\) là
A. \(x = 2\)
B. \(x = {\rm{\;}} - 2\)
C. \(x = 3\)
D. \(x = {\rm{\;}} - 3\)
Câu 3 : Nếu 15 lít dầu nặng 12kg thì 24kg dầu đó sẽ chứa vừa đầy trong thùng
A. 30 lít
B. 27 lít
C. 15 lít
D. 13,5 lít
Câu 4 : Cho x và y tỉ lệ thuận với nhau và khi \(x = {\rm{\;}} - 3\)thì \(y = 12\). Hệ số tỉ lệ k của y đối với x là
A. \(k = {\rm{\;}} - 0,25\)
B. \(k = {\rm{\;}} - 4\)
C. \(k = 0,25\)
D. \(k = 4\)
Câu 5 : Biết rằng \(\dfrac{{ - 3}}{4} = \dfrac{x}{5}\). Khi đó giá trị của x là
A. \(\dfrac{{ - 15}}{4}\)
B. \(\dfrac{{ - 20}}{3}\)
C. \( - 2\)
D. \(2\)
Câu 6 : Mặt bên của hình lăng trụ đứng tam giác là hình gì?
A. Tam giác
B. Hình vuông
C. Hình chữ nhật
D. Hình bình hành
Câu 7 : Cho đường thẳng a cắt hai đường thẳng phân biệt b, c. Số cặp góc đồng vị được tạo ra là
A. 2
B. 3
C. 4
D. 6
Câu 8 : Trong các khẳng định sau khẳng định nào sai?
A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau.
B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\).
C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong của tam giác đó.
D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Câu 9. Thể tích hình hộp chữ nhật có chiều dài 4cm, chiều rộng 3cm, chiều cao 5cm là:
A. 60cm2
B. 60cm3
C. 35cm2
D. 35cm3
Câu 10: Số nào là số vô tỉ trong các số sau:
A. \(\dfrac{2}{3}\)
B. \(\pi \)
C. \( - \sqrt {16} \)
D. 0
Câu 11. Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là 2 góc kề bù. Biết \(\widehat {xOy} = {25^0}\) , số đo\(\widehat {yOz}\) bằng ?
A. 650.
B. 250.
C. 750.
D. 1550.
Câu 12. Cho\(\widehat {xOy} = {70^0}\) , Ot là tia phân giác của \(\widehat {xOy}\) . Số đo \(\widehat {xOt}\) bằng ?
A. 350.
B. 300.
C. 400.
D. 1400.
PHẦN II. TỰ LUẬN (7 điểm)
Câu 1 (1,5 điểm): Thực hiện phép tính:
a) \(\dfrac{7}{6} - \dfrac{1}{6}:\dfrac{2}{3}\)
b) \(1\dfrac{3}{4}.\dfrac{2}{7} - 1\dfrac{3}{4}.\dfrac{5}{7}\)
c) \(0,5\sqrt {100} {\rm{\;}} - \dfrac{1}{4}\sqrt {16} {\rm{\;}} + {\left( {\dfrac{{ - 2}}{3}} \right)^2}\)
Câu 2 (1,5 điểm): Tìm x:
a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)
b) \(\dfrac{1}{6}x - 3 = \dfrac{{ - 2}}{3}\)
c) \({\left( {\dfrac{1}{5} - x} \right)^2} = \dfrac{{16}}{9}\)
Câu 3 (1,5 điểm): Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trồng được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.
Câu 4 (2 điểm)
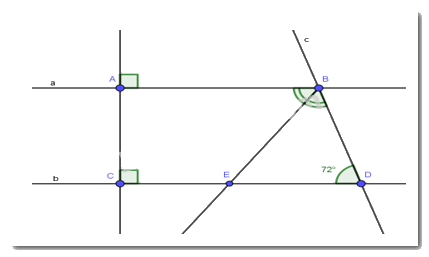
Cho hình vẽ
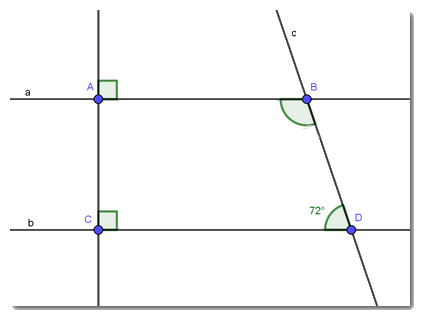
a) Chứng minh AB // CD
b) Tính \(\widehat {ABD}\)
c) Vẽ tia BE là tia phân giác của \(\widehat {ABD}\) (\(E \in CD\)). Tính \(\widehat {ABE}\)?
Câu 5 (0,5 điểm): Cho ba số a, b, c dương. Chứng tỏ rằng \(M = \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không là số nguyên.
I. TRẮC NGHIỆM
1. B | 2. D | 3. A | 4. B | 5. A | 6. C |
7. C | 8. C | 9. B | 10. B | 11. D | 12. A |
Câu 1:
Phương pháp
Quy đồng phân số rồi tiến hành phép cộng hai phân số cùng mẫu.
Lời giải
\(\dfrac{{ - 5}}{{12}} + \dfrac{{ - 1}}{4} = \dfrac{{ - 5}}{{12}} + \dfrac{{ - 3}}{{12}} = \dfrac{{ - 8}}{{12}} = \dfrac{{ - 2}}{3}\)
Chọn B.
Câu 2:
Phương pháp
Với m là số lẻ, nếu \({a^m} = {b^m} \Rightarrow a = b\)
Lời giải
\({x^3} = {\rm{\;}} - 27 \Leftrightarrow {x^3} = {\rm{\;}}{\left( { - 3} \right)^3} \Leftrightarrow x = - 3\)
Vậy \(x = - 3\).
Câu 3:
Phương pháp
Tính chất hai đại lượng tỉ lệ thuận: \(\dfrac{{{x_1}}}{{{y_1}}} = \dfrac{{{x_2}}}{{{y_2}}}\)
Lời giải
Gọi thể tích thùng dầu đựng vừa đủ 24 kg dầu là x (x > 0).
Vì thể tích và khối lượng dầu là hai đại lượng tỉ lệ thuận nên \(\dfrac{{12}}{{15}} = \dfrac{{24}}{x} \Rightarrow 12.x = 15.24 \Rightarrow x = \dfrac{{15.24}}{{12}} = 30\).
Vậy 24 kg dầu đựng vừa đủ trong thùng 30 lít.
Chọn A.
Câu 4:
Phương pháp
Hệ số tỉ lệ của đại lượng y đối với x là: \(k = \dfrac{y}{x}\)
Lời giải
Hệ số tỉ lệ của y đối với x là: \(k = \dfrac{{12}}{{ - 3}} = - 4\).
Chọn B.
Câu 5:
Phương pháp
Tính chất của tỉ lệ thức: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a.d = b.c\)
Lời giải
\(\dfrac{{ - 3}}{4} = \dfrac{x}{5} \Rightarrow ( - 3).5 = 4.x \Rightarrow x = \dfrac{{ - 15}}{4}\)
Chọn A.
Câu 6:
Phương pháp
Tính chất của hình lăng trụ đứng tam giác.
Lời giải
Mặt bên của hình lăng trụ đứng tam giác là hình chữ nhật.
Chọn C.
Câu 7:
Phương pháp
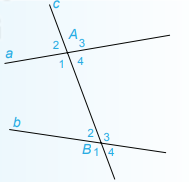
+ Các cặp góc A1 và B1 ; A2 và B2 ; A3 và B3 ; A4 và B4 được gọi là các cặp góc đồng vị
Lời giải
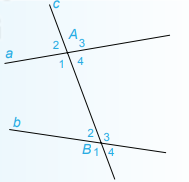
Đường thẳng a cắt hai đường thẳng phân biệt b, c tạo thành 4 cặp góc đồng vị, 2 cặp góc so le trong.
Chọn C.
Câu 8:
Phương pháp
Tính chất và dấu hiệu nhận biết hai đường thẳng song song.
Tính chất hai góc kề bù và tia phân giác của một góc.
Lời giải
Xét A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau nên A đúng.
Xét B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\) nên B đúng.
Xét C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó nên C sai.
Xét D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông nên D đúng.
Chọn C.
Câu 9:
Phương pháp
Thể tích hình hộp chữ nhật có kích thước a,b,c là: V = a.b.c
Lời giải
Thể tích hình hộp chữ nhật đó là: V = 4.3.5=60 (cm3)
Chọn B.
Câu 10:
Phương pháp
Viết các số dưới dạng số thập phân
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn
Lời giải
Số \(\pi = 3,141592654.....\) là số thập phân vô hạn không tuần hoàn nên là số vô tỉ.
Chọn B.
Câu 11:
Phương pháp
Hai góc kề bù có tổng số đo bằng 180 độ.
Lời giải
Ta có: \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) (2 góc kề bù) nên \(25^\circ + \widehat {yOz} = 180^\circ \Rightarrow \widehat {yOz} = 180^\circ - 25^\circ = 155^\circ \)
Chọn D.
Câu 11:
Phương pháp
Nếu Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}.\widehat {xOy}\)
Lời giải
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}.\widehat {xOy} = \dfrac{1}{2}.70^\circ = 35^\circ \)
Chọn A.
II. TỰ LUẬN
Câu 1:
Thực hiện phép tính:
a) \(\dfrac{7}{6} - \dfrac{1}{6}:\dfrac{2}{3} = \dfrac{7}{6} - \dfrac{1}{6}.\dfrac{3}{2} = \dfrac{7}{6} - \dfrac{1}{4} = \dfrac{{7.2 - 1.3}}{{12}} = \dfrac{{11}}{{12}}\)
b) \(1\dfrac{3}{4}.\dfrac{2}{7} - 1\dfrac{3}{4}.\dfrac{5}{7} = \dfrac{7}{4}.\dfrac{2}{7} - \dfrac{7}{4}.\dfrac{5}{7} = \dfrac{2}{4} - \dfrac{5}{4} = {\rm{\;}} - \dfrac{3}{4}\)
c) \(0,5\sqrt {100} {\rm{\;}} - \dfrac{1}{4}\sqrt {16} {\rm{\;}} + {\left( {\dfrac{{ - 2}}{3}} \right)^2}\)
\( = 0,5.10 - \dfrac{1}{4}.4 + \dfrac{4}{9} = 5 - 1 + \dfrac{4}{9}\)
\( = 4 + \dfrac{4}{9} = \dfrac{{4.9 + 4}}{9} = \dfrac{{40}}{9}\)
Câu 2:
Tìm x:
a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)
\( \Leftrightarrow x = \dfrac{3}{{10}} - \dfrac{2}{5} = \dfrac{{3 - 2.2}}{{10}} = \dfrac{{ - 1}}{{10}}\)
b) \(\dfrac{1}{6}x - 3 = \dfrac{{ - 2}}{3}\)
\( \Leftrightarrow \dfrac{1}{6}x = \dfrac{{ - 2}}{3} + 3 = \dfrac{7}{3}\)
\( \Leftrightarrow x = \dfrac{7}{3}.6 = 14\)
c) \({\left( {\dfrac{1}{5} - x} \right)^2} = \dfrac{{16}}{9}\)
\( \Leftrightarrow \left| {\dfrac{1}{5} - x} \right| = \dfrac{4}{3}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\dfrac{1}{5} - x = \dfrac{4}{3}}\\{\dfrac{1}{5} - x = {\rm{\;}} - \dfrac{4}{3}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \dfrac{1}{5} - \dfrac{4}{3}}\\{x = \dfrac{1}{5} + \dfrac{4}{3}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{\;}} - \dfrac{{17}}{{15}}}\\{x = \dfrac{{23}}{{15}}}\end{array}} \right..\)
\(\begin{array}{*{20}{l}}{d)\;\;\dfrac{{x - 1}}{6} = \dfrac{{x + 3}}{5}}\\{ \Leftrightarrow 5.\left( {x - 1} \right) = 6.\left( {x + 3} \right)}\\{ \Leftrightarrow 5x - 5 = 6x + 18}\\{ \Leftrightarrow 6x - 5x = {\rm{\;}} - 5 - 18}\\{ \Leftrightarrow x = {\rm{\;}} - 23}\end{array}\)
Câu 3:
Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trông được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là x, y, z(cây) (\(x,y,z \in {N^*}\))
Ba lớp 7A, 7B, 7C trồng được 180 cây nên \(x + y + z = 180\)
Số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5 nên ta có:
\(x:y:z = 3:4:5\)
\( \Leftrightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = \dfrac{{x + y + z}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\) (Áp dụng tính chất dãy tỉ số bằng nhau)
\( \Rightarrow x = 15.3 = 45{\mkern 1mu} {\mkern 1mu} \)(cây) \(;{\mkern 1mu} {\mkern 1mu} y = 15.4 = 60\) (cây) \(;{\mkern 1mu} {\mkern 1mu} z = 15.5 = 75\) (cây)
Vậy lớp 7A trồng 45 cây, lớp 7B trồng được 60 cây, lớp 7C trồng được 75 cây.
Câu 4:
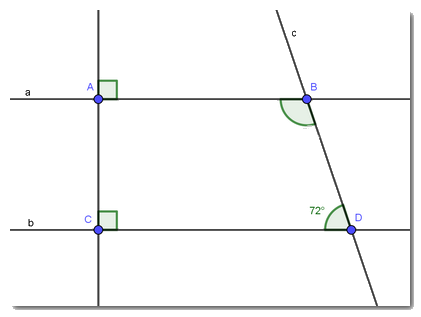
a) Ta có AB\( \bot \) AC (gt)
CD \( \bot \) AC (gt)
\( \Rightarrow \) AB // CD
b) Ta có \(\widehat {ABD} + \widehat {BDC} = {180^0}\) (vì AB // CD)
hay\(\widehat {ABD} + {72^0} = {180^0}\)
\( \Rightarrow \widehat {ABD} = {108^0}\)
c)
Vì BE là tia phân giác của \(\widehat {ABD}\)
Nên \(\widehat {ABE} = \dfrac{{\widehat {ABD}}}{2} = \dfrac{{{{108}^0}}}{2} = {54^0}\)
Câu 5:
Ta có:
\(\begin{array}{*{20}{l}}{\dfrac{a}{{a + b}} > \dfrac{a}{{a + b + c}}}\\{\dfrac{b}{{b + c}} > \dfrac{b}{{a + b + c}}}\\{\dfrac{c}{{c + a}} > \dfrac{c}{{a + b + c}}}\end{array}\)
Cộng vế với vế ta được:
\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} > \dfrac{a}{{a + b + c}} + \dfrac{b}{{a + b + c}} + \dfrac{c}{{a + b + c}}\)\({\mkern 1mu} \left( { = \dfrac{{a + b + c}}{{a + b + c}} = 1} \right)\) (1)
Lại có:
\(\begin{array}{*{20}{l}}{\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}}\\{\dfrac{b}{{b + c}} < \dfrac{{b + a}}{{a + b + c}}}\\{\dfrac{c}{{c + a}} < \dfrac{{c + b}}{{a + b + c}}}\end{array}\)
Cộng vế với vế ta được:
\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < \dfrac{{a + c}}{{a + b + c}} + \dfrac{{b + a}}{{a + b + c}} + \dfrac{{c + b}}{{a + b + c}}\)\({\mkern 1mu} \left( { = \dfrac{{2(a + b + c)}}{{a + b + c}} = 2} \right)\) (2)
Từ (1) và (2) ta có: \(1 < \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < 2\)
\( \Rightarrow \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không phải là số nguyên (đpcm).
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 : Kết quả phép tính \(\dfrac{{ - 5}}{{12}} + \dfrac{{ - 1}}{4}\) bằng
A. \(\dfrac{{ - 1}}{2}\)
B. \(\dfrac{{ - 2}}{3}\)
C. \(\dfrac{1}{2}\)
D. \(\dfrac{2}{3}\)
Câu 2 : Giá trị của x thỏa mãn đẳng thức \({x^3} = {\rm{\;}} - 27\) là
A. \(x = 2\)
B. \(x = {\rm{\;}} - 2\)
C. \(x = 3\)
D. \(x = {\rm{\;}} - 3\)
Câu 3 : Nếu 15 lít dầu nặng 12kg thì 24kg dầu đó sẽ chứa vừa đầy trong thùng
A. 30 lít
B. 27 lít
C. 15 lít
D. 13,5 lít
Câu 4 : Cho x và y tỉ lệ thuận với nhau và khi \(x = {\rm{\;}} - 3\)thì \(y = 12\). Hệ số tỉ lệ k của y đối với x là
A. \(k = {\rm{\;}} - 0,25\)
B. \(k = {\rm{\;}} - 4\)
C. \(k = 0,25\)
D. \(k = 4\)
Câu 5 : Biết rằng \(\dfrac{{ - 3}}{4} = \dfrac{x}{5}\). Khi đó giá trị của x là
A. \(\dfrac{{ - 15}}{4}\)
B. \(\dfrac{{ - 20}}{3}\)
C. \( - 2\)
D. \(2\)
Câu 6 : Mặt bên của hình lăng trụ đứng tam giác là hình gì?
A. Tam giác
B. Hình vuông
C. Hình chữ nhật
D. Hình bình hành
Câu 7 : Cho đường thẳng a cắt hai đường thẳng phân biệt b, c. Số cặp góc đồng vị được tạo ra là
A. 2
B. 3
C. 4
D. 6
Câu 8 : Trong các khẳng định sau khẳng định nào sai?
A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau.
B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\).
C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong của tam giác đó.
D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Câu 9. Thể tích hình hộp chữ nhật có chiều dài 4cm, chiều rộng 3cm, chiều cao 5cm là:
A. 60cm2
B. 60cm3
C. 35cm2
D. 35cm3
Câu 10: Số nào là số vô tỉ trong các số sau:
A. \(\dfrac{2}{3}\)
B. \(\pi \)
C. \( - \sqrt {16} \)
D. 0
Câu 11. Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là 2 góc kề bù. Biết \(\widehat {xOy} = {25^0}\) , số đo\(\widehat {yOz}\) bằng ?
A. 650.
B. 250.
C. 750.
D. 1550.
Câu 12. Cho\(\widehat {xOy} = {70^0}\) , Ot là tia phân giác của \(\widehat {xOy}\) . Số đo \(\widehat {xOt}\) bằng ?
A. 350.
B. 300.
C. 400.
D. 1400.
PHẦN II. TỰ LUẬN (7 điểm)
Câu 1 (1,5 điểm): Thực hiện phép tính:
a) \(\dfrac{7}{6} - \dfrac{1}{6}:\dfrac{2}{3}\)
b) \(1\dfrac{3}{4}.\dfrac{2}{7} - 1\dfrac{3}{4}.\dfrac{5}{7}\)
c) \(0,5\sqrt {100} {\rm{\;}} - \dfrac{1}{4}\sqrt {16} {\rm{\;}} + {\left( {\dfrac{{ - 2}}{3}} \right)^2}\)
Câu 2 (1,5 điểm): Tìm x:
a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)
b) \(\dfrac{1}{6}x - 3 = \dfrac{{ - 2}}{3}\)
c) \({\left( {\dfrac{1}{5} - x} \right)^2} = \dfrac{{16}}{9}\)
Câu 3 (1,5 điểm): Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trồng được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.
Câu 4 (2 điểm)
Cho hình vẽ
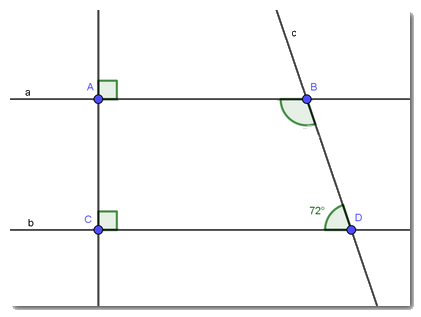
a) Chứng minh AB // CD
b) Tính \(\widehat {ABD}\)
c) Vẽ tia BE là tia phân giác của \(\widehat {ABD}\) (\(E \in CD\)). Tính \(\widehat {ABE}\)?
Câu 5 (0,5 điểm): Cho ba số a, b, c dương. Chứng tỏ rằng \(M = \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không là số nguyên.
I. TRẮC NGHIỆM
1. B | 2. D | 3. A | 4. B | 5. A | 6. C |
7. C | 8. C | 9. B | 10. B | 11. D | 12. A |
Câu 1:
Phương pháp
Quy đồng phân số rồi tiến hành phép cộng hai phân số cùng mẫu.
Lời giải
\(\dfrac{{ - 5}}{{12}} + \dfrac{{ - 1}}{4} = \dfrac{{ - 5}}{{12}} + \dfrac{{ - 3}}{{12}} = \dfrac{{ - 8}}{{12}} = \dfrac{{ - 2}}{3}\)
Chọn B.
Câu 2:
Phương pháp
Với m là số lẻ, nếu \({a^m} = {b^m} \Rightarrow a = b\)
Lời giải
\({x^3} = {\rm{\;}} - 27 \Leftrightarrow {x^3} = {\rm{\;}}{\left( { - 3} \right)^3} \Leftrightarrow x = - 3\)
Vậy \(x = - 3\).
Câu 3:
Phương pháp
Tính chất hai đại lượng tỉ lệ thuận: \(\dfrac{{{x_1}}}{{{y_1}}} = \dfrac{{{x_2}}}{{{y_2}}}\)
Lời giải
Gọi thể tích thùng dầu đựng vừa đủ 24 kg dầu là x (x > 0).
Vì thể tích và khối lượng dầu là hai đại lượng tỉ lệ thuận nên \(\dfrac{{12}}{{15}} = \dfrac{{24}}{x} \Rightarrow 12.x = 15.24 \Rightarrow x = \dfrac{{15.24}}{{12}} = 30\).
Vậy 24 kg dầu đựng vừa đủ trong thùng 30 lít.
Chọn A.
Câu 4:
Phương pháp
Hệ số tỉ lệ của đại lượng y đối với x là: \(k = \dfrac{y}{x}\)
Lời giải
Hệ số tỉ lệ của y đối với x là: \(k = \dfrac{{12}}{{ - 3}} = - 4\).
Chọn B.
Câu 5:
Phương pháp
Tính chất của tỉ lệ thức: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a.d = b.c\)
Lời giải
\(\dfrac{{ - 3}}{4} = \dfrac{x}{5} \Rightarrow ( - 3).5 = 4.x \Rightarrow x = \dfrac{{ - 15}}{4}\)
Chọn A.
Câu 6:
Phương pháp
Tính chất của hình lăng trụ đứng tam giác.
Lời giải
Mặt bên của hình lăng trụ đứng tam giác là hình chữ nhật.
Chọn C.
Câu 7:
Phương pháp
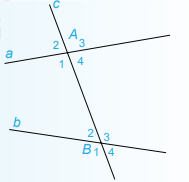
+ Các cặp góc A1 và B1 ; A2 và B2 ; A3 và B3 ; A4 và B4 được gọi là các cặp góc đồng vị
Lời giải
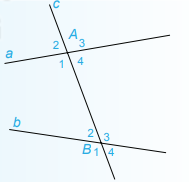
Đường thẳng a cắt hai đường thẳng phân biệt b, c tạo thành 4 cặp góc đồng vị, 2 cặp góc so le trong.
Chọn C.
Câu 8:
Phương pháp
Tính chất và dấu hiệu nhận biết hai đường thẳng song song.
Tính chất hai góc kề bù và tia phân giác của một góc.
Lời giải
Xét A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau nên A đúng.
Xét B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\) nên B đúng.
Xét C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó nên C sai.
Xét D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông nên D đúng.
Chọn C.
Câu 9:
Phương pháp
Thể tích hình hộp chữ nhật có kích thước a,b,c là: V = a.b.c
Lời giải
Thể tích hình hộp chữ nhật đó là: V = 4.3.5=60 (cm3)
Chọn B.
Câu 10:
Phương pháp
Viết các số dưới dạng số thập phân
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn
Lời giải
Số \(\pi = 3,141592654.....\) là số thập phân vô hạn không tuần hoàn nên là số vô tỉ.
Chọn B.
Câu 11:
Phương pháp
Hai góc kề bù có tổng số đo bằng 180 độ.
Lời giải
Ta có: \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) (2 góc kề bù) nên \(25^\circ + \widehat {yOz} = 180^\circ \Rightarrow \widehat {yOz} = 180^\circ - 25^\circ = 155^\circ \)
Chọn D.
Câu 11:
Phương pháp
Nếu Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}.\widehat {xOy}\)
Lời giải
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}.\widehat {xOy} = \dfrac{1}{2}.70^\circ = 35^\circ \)
Chọn A.
II. TỰ LUẬN
Câu 1:
Thực hiện phép tính:
a) \(\dfrac{7}{6} - \dfrac{1}{6}:\dfrac{2}{3} = \dfrac{7}{6} - \dfrac{1}{6}.\dfrac{3}{2} = \dfrac{7}{6} - \dfrac{1}{4} = \dfrac{{7.2 - 1.3}}{{12}} = \dfrac{{11}}{{12}}\)
b) \(1\dfrac{3}{4}.\dfrac{2}{7} - 1\dfrac{3}{4}.\dfrac{5}{7} = \dfrac{7}{4}.\dfrac{2}{7} - \dfrac{7}{4}.\dfrac{5}{7} = \dfrac{2}{4} - \dfrac{5}{4} = {\rm{\;}} - \dfrac{3}{4}\)
c) \(0,5\sqrt {100} {\rm{\;}} - \dfrac{1}{4}\sqrt {16} {\rm{\;}} + {\left( {\dfrac{{ - 2}}{3}} \right)^2}\)
\( = 0,5.10 - \dfrac{1}{4}.4 + \dfrac{4}{9} = 5 - 1 + \dfrac{4}{9}\)
\( = 4 + \dfrac{4}{9} = \dfrac{{4.9 + 4}}{9} = \dfrac{{40}}{9}\)
Câu 2:
Tìm x:
a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)
\( \Leftrightarrow x = \dfrac{3}{{10}} - \dfrac{2}{5} = \dfrac{{3 - 2.2}}{{10}} = \dfrac{{ - 1}}{{10}}\)
b) \(\dfrac{1}{6}x - 3 = \dfrac{{ - 2}}{3}\)
\( \Leftrightarrow \dfrac{1}{6}x = \dfrac{{ - 2}}{3} + 3 = \dfrac{7}{3}\)
\( \Leftrightarrow x = \dfrac{7}{3}.6 = 14\)
c) \({\left( {\dfrac{1}{5} - x} \right)^2} = \dfrac{{16}}{9}\)
\( \Leftrightarrow \left| {\dfrac{1}{5} - x} \right| = \dfrac{4}{3}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\dfrac{1}{5} - x = \dfrac{4}{3}}\\{\dfrac{1}{5} - x = {\rm{\;}} - \dfrac{4}{3}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \dfrac{1}{5} - \dfrac{4}{3}}\\{x = \dfrac{1}{5} + \dfrac{4}{3}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{\;}} - \dfrac{{17}}{{15}}}\\{x = \dfrac{{23}}{{15}}}\end{array}} \right..\)
\(\begin{array}{*{20}{l}}{d)\;\;\dfrac{{x - 1}}{6} = \dfrac{{x + 3}}{5}}\\{ \Leftrightarrow 5.\left( {x - 1} \right) = 6.\left( {x + 3} \right)}\\{ \Leftrightarrow 5x - 5 = 6x + 18}\\{ \Leftrightarrow 6x - 5x = {\rm{\;}} - 5 - 18}\\{ \Leftrightarrow x = {\rm{\;}} - 23}\end{array}\)
Câu 3:
Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trông được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là x, y, z(cây) (\(x,y,z \in {N^*}\))
Ba lớp 7A, 7B, 7C trồng được 180 cây nên \(x + y + z = 180\)
Số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5 nên ta có:
\(x:y:z = 3:4:5\)
\( \Leftrightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = \dfrac{{x + y + z}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\) (Áp dụng tính chất dãy tỉ số bằng nhau)
\( \Rightarrow x = 15.3 = 45{\mkern 1mu} {\mkern 1mu} \)(cây) \(;{\mkern 1mu} {\mkern 1mu} y = 15.4 = 60\) (cây) \(;{\mkern 1mu} {\mkern 1mu} z = 15.5 = 75\) (cây)
Vậy lớp 7A trồng 45 cây, lớp 7B trồng được 60 cây, lớp 7C trồng được 75 cây.
Câu 4:
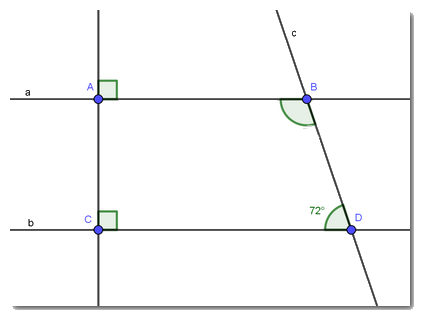
a) Ta có AB\( \bot \) AC (gt)
CD \( \bot \) AC (gt)
\( \Rightarrow \) AB // CD
b) Ta có \(\widehat {ABD} + \widehat {BDC} = {180^0}\) (vì AB // CD)
hay\(\widehat {ABD} + {72^0} = {180^0}\)
\( \Rightarrow \widehat {ABD} = {108^0}\)
c)
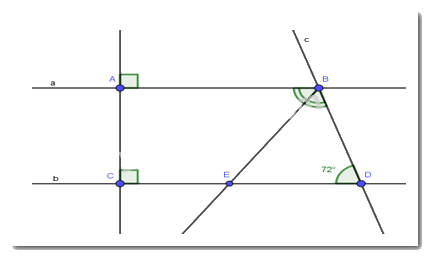
Vì BE là tia phân giác của \(\widehat {ABD}\)
Nên \(\widehat {ABE} = \dfrac{{\widehat {ABD}}}{2} = \dfrac{{{{108}^0}}}{2} = {54^0}\)
Câu 5:
Ta có:
\(\begin{array}{*{20}{l}}{\dfrac{a}{{a + b}} > \dfrac{a}{{a + b + c}}}\\{\dfrac{b}{{b + c}} > \dfrac{b}{{a + b + c}}}\\{\dfrac{c}{{c + a}} > \dfrac{c}{{a + b + c}}}\end{array}\)
Cộng vế với vế ta được:
\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} > \dfrac{a}{{a + b + c}} + \dfrac{b}{{a + b + c}} + \dfrac{c}{{a + b + c}}\)\({\mkern 1mu} \left( { = \dfrac{{a + b + c}}{{a + b + c}} = 1} \right)\) (1)
Lại có:
\(\begin{array}{*{20}{l}}{\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}}\\{\dfrac{b}{{b + c}} < \dfrac{{b + a}}{{a + b + c}}}\\{\dfrac{c}{{c + a}} < \dfrac{{c + b}}{{a + b + c}}}\end{array}\)
Cộng vế với vế ta được:
\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < \dfrac{{a + c}}{{a + b + c}} + \dfrac{{b + a}}{{a + b + c}} + \dfrac{{c + b}}{{a + b + c}}\)\({\mkern 1mu} \left( { = \dfrac{{2(a + b + c)}}{{a + b + c}} = 2} \right)\) (2)
Từ (1) và (2) ta có: \(1 < \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < 2\)
\( \Rightarrow \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không phải là số nguyên (đpcm).
Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một học kỳ học tập. Đề thi bao gồm các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Đề thi thường được chia thành các phần:
Phần này thường tập trung vào các khái niệm cơ bản về số hữu tỉ, số thực, cách biểu diễn trên trục số, các phép toán trên số hữu tỉ và số thực. Học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ và số thực, cũng như các tính chất của phép toán.
Học sinh cần hiểu rõ khái niệm biểu thức đại số, cách thu gọn biểu thức, các quy tắc cộng, trừ, nhân, chia đa thức. Phần này cũng thường yêu cầu học sinh vận dụng các hằng đẳng thức đáng nhớ để giải các bài toán.
Đây là một trong những chủ đề quan trọng nhất của chương trình Toán 7. Học sinh cần nắm vững định nghĩa phương trình bậc nhất một ẩn, cách giải phương trình, các ứng dụng của phương trình trong thực tế.
Học sinh cần hiểu rõ khái niệm bất đẳng thức, các quy tắc chuyển vế, cộng trừ bất đẳng thức, các ứng dụng của bất đẳng thức trong thực tế.
Phần này thường yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán thực tế, giúp học sinh hiểu rõ hơn về tầm quan trọng của toán học trong cuộc sống.
Để giải tốt đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều, học sinh cần:
Ngoài việc giải đề thi, học sinh có thể tham khảo các tài liệu ôn tập sau:
Hãy dành thời gian ôn tập kỹ lưỡng trước khi thi. Đừng ngại hỏi thầy cô hoặc bạn bè nếu có bất kỳ thắc mắc nào. Chúc các em học sinh đạt kết quả tốt trong kỳ thi học kì 1!
Bài 1: Giải phương trình 2x + 5 = 11
Lời giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 6 / 2
x = 3
Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều là một bài kiểm tra quan trọng, đòi hỏi học sinh phải có sự chuẩn bị kỹ lưỡng. Hy vọng với những phân tích và hướng dẫn giải chi tiết trên đây, các em học sinh sẽ tự tin hơn khi bước vào kỳ thi.