Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 7 - Đề số 4 - Cánh diều, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học mới, bám sát nội dung sách giáo khoa Cánh diều.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết các bài toán thực tế. Hãy cùng Giaitoan.edu.vn chinh phục kỳ thi học kì 2 Toán 7 một cách tự tin nhất!
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
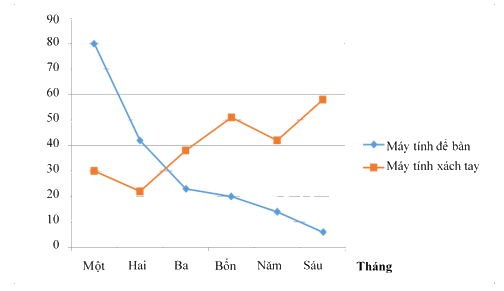
Câu 1. Cho biểu đồ đoạn thẳng. Em hãy cho biết nhu cầu bán máy tính để bàn, máy tính xách tay tăng hay giảm trong 6 tháng?
A. Máy tính để bàn tăng, máy tính xách tay tăng
B. Máy tính để bàn tăng, máy tính xách tay giảm
C. Máy tính để bàn giảm, máy tính xách tay tăng
D. Máy tính để bàn giảm, máy tính xách tay giảm
Câu 2. Trong các sự kiện, hiện tượng sau, đâu là biến cố chắc chắn?
A. Mặt Trời quay quanh Trái Đất
B. Khi gieo đồng xu thì được mặt ngửa
C. Có 9 cơn bão đổ bộ vào nước ta trong năm tới
D. Ngày mai, Mặt Trời mọc ở phía Đông
Câu 3. Giá trị của biểu thức: \({x^3} - 2{x^2}\) tại \(x = - 2\) là:
A. \( - 16\)
B. \(16\)
C. \(0\)
D. \( - 8\)
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. \(4{x^2}y\left( { - 2x} \right)\)
B. \(2x\)
C. \(2xy - {x^2}\)
D. \(2021\)
Câu 5. Sắp xếp các hạng tử của đa thức \(P\left( x \right) = 2{x^3} - 7{x^2} + {x^4} - 4\) theo lũy thừa giảm dần của biến ta được:
A. \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
B. \(P\left( x \right) = 7{x^2} + 2{x^3} + {x^4} - 4\)
C. \(P\left( x \right) = - 4 - 7{x^2} + 2{x^3} + {x^4}\)
D. \(P\left( x \right) = {x^4} - 2{x^3} - 7{x^2} - 4\)
Câu 6. Cho tam giác \(MNP\) có \(NP = 1cm,MP = 7cm\). Độ dài cạnh \(MN\) là một số nguyên (cm). Độ dài cạnh \(MN\) là:
A. \(8cm\)
B. \(5cm\)
C. \(6cm\)
D. \(7cm\)
Câu 7. Cho tam giác ABC có \(AB = AC.\) Trên các cạnh AB và AC lấy các điểm D,E sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của BE và CD. Chọn câu sai.
A. \(BE = CD\)
B. \(BK = KC\)
C. \(BD = CE\)
D. \(DK = KC\)
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Một khối 7 trường THCS có 200 học sinh đăng ký thực đơn ăn trưa gồm 4 món: Pizza; mỳ Ý; Hamburger; Donut. Số phần trăm học sinh chọn Pizza là \(12,5\% \); số học sinh chọn mỳ Ý chiếm \(30\% \); số học sinh chọn bánh Hamburger chiếm một nửa tổng số học sinh khối 7. Còn lại số học sinh chọn bánh Donut.
a) Tính tỉ số phần trăm số học sinh chọn Piza và tỉ số phần trăm số học sinh chọn Donut
b) Lập bảng số liệu học sinh chọn từng loại thức ăn cho bữa trưa (đơn vị học sinh).
Bài 2. (2,5 điểm) Cho hai đa thức: \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\) và \(g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\).
a) Thu gọn và sắp xếp hai đa thức \(f\left( x \right)\) và \(g\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) và tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\).
Bài 3. (3,5 điểm) Cho tam giác ABC vuông tại A.
a) Tia phân giác của góc B cắt cạnh AC ở D. Kẻ DE vuông góc với BC tại E.
Chứng minh rằng ΔABD = ΔEBD.
b) So sánh AD và DC.
c) Tia ED cắt BA tại G. Gọi I là trung điểm GC. Chứng minh rằng B, D, I thẳng hàng.
Bài 4. (0,5 điểm) Cho \(x;{\kern 1pt} y;{\kern 1pt} z\) tỉ lệ thuận với \(3;{\kern 1pt} \,4;\,{\kern 1pt} 5.\) Tính giá trị của biểu thức
\(A = 2024\left( {x - y} \right)\left( {y - z} \right) - 506.{\left( {\dfrac{{x + y + z}}{6}} \right)^2}\)
I. Trắc nghiệm
1. C | 2. D | 3. A | 4. C |
5. A | 6. D | 7. D | 8. C |
Câu 1.
Phương pháp:
Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của số liệu trong một khoảng thời gian nhất định.
Cách giải:
Nhu cầu bán máy tính để bàn giảm mạnh trong 6 tháng,
Nhu cầu bán máy tính xách tay tăng mạnh trong 6 tháng.
Chọn C.
Câu 2.
Phương pháp:
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra
Cách giải:
Đáp án ABiến cố không thể
Đáp án BBiến cố ngẫu nhiên
Đáp án CBiến cố ngẫu nhiên
Đáp án DMặt Trời luôn mọc ở phía Đông nên sự kiện “Ngày mai, Mặt Trời mọc ở phía Đông." Luôn xảy ra nên là biến
cố chắc chắn.
Chọn D.
Câu 3.
Phương pháp:
Thay \(x = - 2\) vào biểu thức \({x^3} - 2{x^2}\) để tính.
Cách giải:
Thay \(x = - 2\) vào biểu thức \({x^3} - 2{x^2}\) ta có: \({\left( { - 2} \right)^3} - 2.{\left( { - 2} \right)^2} = \left( { - 8} \right) - 2.4 = - 16\)
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: \(2xy - {x^2}\) không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến: \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là \(a,b,c\) nếu \(\left| {b - c} \right| < a < b + c\).
+ Trong trường hợp xác định được \(a\) là số lớn nhất trong ba số \(a,b,c\) thì điều kiện tồn tại tam giác là \(a < b + c\).
Cách giải:
Xét tam giác \(MNP\), ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {NP - MP} \right| < MN < NP + MP\\ \Rightarrow \left| {1 - 7} \right| < MN < 1 + 7\\ \Rightarrow 6 < MN < 8\end{array}\)
Vì độ dài cạnh \(MN\) là một số nguyên nên \(MN = 7\,\left( {cm} \right)\)
Chọn D.
Câu 7.
Phương pháp:
Dựa vào tính chất hai tam giác bằng nhau .
Cách giải:
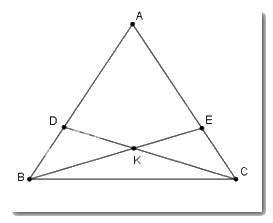
Xét tam giác ABE và tam giác ADC có
+ AD = AE (GT)
+ Góc A chung
+ AB = AC (GT)
Suy ra \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\) \( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và BE = CD (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = {180^\circ }\); \(\widehat {AEB} + \widehat {BEC} = {180^\circ }\) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
Suy ra \(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;{\mkern 1mu} AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nênC đúng.
Xét tam giác KBD và tam giác KCE có
+ \(\widehat {ABE} = \widehat {ACD}{\mkern 1mu} \left( {cmt} \right)\)
+ \(BD = EC{\mkern 1mu} \left( {cmt} \right)\)
+ \(\widehat {BDC} = \widehat {BEC}{\mkern 1mu} \left( {cmt} \right)\)
Nên \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\) \( \Rightarrow KB = KC;{\mkern 1mu} KD = KE\) (hai cạnh tương ứng) nên Bđúng, D sai.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp
a) Tổng số học sinh của trường được coi là \(100\% \), nửa tổng số học sinh là \(50\% .\)
b) Áp dụng công thức tính tỉ số phần trăm: Muốn tìm \(a\,\% \)của \(b\) ta tính \(b.\dfrac{a}{{100}}\)
Cách giải:
a) Vì số học sinh chọn bánh Hamburger chiếm một nửa tổng số học sinh khối \(7\), nên tỉ số phấn trăm số học sinh chọn bánh Hamburger là \(50\% .\)
Tỉ số phần trăm số học sinh chọn bánh Donut là: \(100\% - 12,5\% - 50\% - 30\% = 7,5\% .\)
b) Số học sinh chọn Piza là: \(200.\dfrac{{12,5}}{{100}} = 25\) (học sinh).
Số học sinh chọn Mỳ Ý là: \(200.\dfrac{{30}}{{100}} = 60\) (học sinh).
Số học sinh chọn bánh Hamburger là: \(200.\dfrac{{50}}{{100}} = 100\) (học sinh).
Số học sinh chọn bánh Donut là: \(200 - 25 - 60 - 100 = 15\) (học sinh).
Bảng số liệu: Số học sinh đăng ký thực đơn ăn trưa:
Đăng ký món | Piza | Mỳ Ý | Hambuger | Donut |
Số lượng (học sinh) | \(25\) | \(60\) | \(100\) | \(15\) |
Bài 2.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\), ta giải phương trình \(f\left( x \right) + g\left( x \right) = 0\)
Cách giải:
a) \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\)
\(\begin{array}{l}f\left( x \right) = \left( {{x^5} - {x^5}} \right) + {x^3} + \left( { - 4x + 3x} \right) + 7\\f\left( x \right) = {x^3} - x + 7\end{array}\)
\(\begin{array}{l}g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\\g\left( x \right) = - {x^3} + \left( {3{x^2} - 3{x^2}} \right) + 8x - 14\\g\left( x \right) = - {x^3} + 8x - 14\end{array}\)
b) \(f\left( x \right) + g\left( x \right) = {x^3} - x + 7 - {x^3} + 8x - 14\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^3} - x + 7 - {x^3} + 8x - 14\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x^3} - {x^3}} \right) + \left( { - x + 8x} \right) + \left( {7 - 14} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 7x - 7\end{array}\)
Ta có: \(f\left( x \right) + g\left( x \right) = 0\)
\(\begin{array}{l}7x - 7 = 0\\7x = 7\\\,\,\,x = 1\end{array}\)
Vậy \(x = 1\) là nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\)
Bài 3.
Phương pháp:
Sử dụng tính chất tia phân giác, các phương pháp chứng minh hai tam giác vuông bằng nhau, mối quan hệ giữa cạnh và góc trong tam giác, tính chất của tam giác cân.
Cách giải:
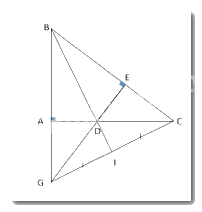
a) Chứng minh rằng ΔABD = ΔEBD.
Xét hai tam giác vuông ΔABD và ΔEBD ta có:
\(\angle A = \angle E = {90^0}\)
AD = DE (vì BD là tia phân giác)
BD cạnh chung
Suy ra ΔABD = ΔEBD (cạnh huyền – cạnh góc vuông) \( \Rightarrow \)AD = DE, BA = BE (cạnh tương ứng) (1)
b) So sánh AD và DC
Xét ΔDEC vuông tại E ta có: DC > DE
Lại có AD = DE (cmt)
\( \Rightarrow \)DC > AD
c) Chứng minh rằng B, D, I thẳng hàng.
Xét ΔBGC có AC \( \bot \) AB, GE \( \bot \) AC
Suy ra D là trực tâm của ΔBGC.(2)
Xét hai tam giác vuông ΔADG và ΔEDC ta có:
\(\angle \)ADG = \(\angle \)EDC (đối đỉnh)
\(\angle A = \angle E = \angle {90^0}\)
AD = DE (cm câu b))
Suy ra ΔADG = ΔEDC (cạnh gv – góc nhọn)
\( \Rightarrow \)AG = EC (cạnh tương ứng) (3)
từ (1), (3) suy ra BA +AG = BE + EC\( \Leftrightarrow \) BG = BC
Vậy ΔBGC là tam giác cân tại B. (4)
Từ (2), (4) suy ra BD là đường trung tuyến của tam giác ΔBGC. Hay B, D, I thẳng hàng. (đpcm)
Bài 4.
Phương pháp:
- Bước 1: Từ đề bài suy ra tỉ lệ
- Bước 2: Đặt các tỉ lệ bằng \(k\) từ đó suy ra \(x,{\kern 1pt} y,{\kern 1pt} z\) theo \(k\)
- Bước 3: Thay vào đề bài và tính toán
- Bước 4: Kết luận
Cách giải:
Vì \(x;\,{\kern 1pt} y;{\kern 1pt} \,z\) tỉ lệ thuận với \(3;{\kern 1pt} \,\,4;\,\,{\kern 1pt} 5\) \( \Rightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}\). Đặt \(\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3k}\\{y = 4k}\\{z = 5k}\end{array}} \right.\). Khi đó,\(A = 2024\left( {3k - 4k} \right)\left( {4k - 5k} \right) - 506.{\left( {\dfrac{{3k + 4k + 5k}}{6}} \right)^2}\)
\(A = 2024\left( { - k} \right)\left( { - k} \right) - 506.{\left( {2k} \right)^2}\)
\(A = 2024.{k^2} - 506.4.{k^2}\)
\(A = 2024{k^2} - 2024{k^2}\)
\(A = 0\)
Vậy \(A = 0.\)
Tải về
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
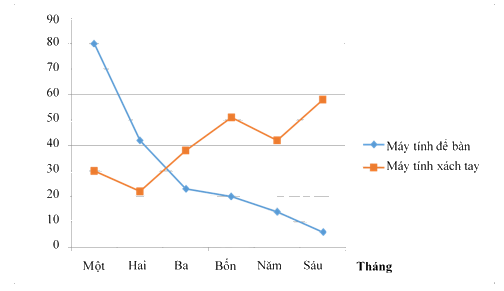
Câu 1. Cho biểu đồ đoạn thẳng. Em hãy cho biết nhu cầu bán máy tính để bàn, máy tính xách tay tăng hay giảm trong 6 tháng?
A. Máy tính để bàn tăng, máy tính xách tay tăng
B. Máy tính để bàn tăng, máy tính xách tay giảm
C. Máy tính để bàn giảm, máy tính xách tay tăng
D. Máy tính để bàn giảm, máy tính xách tay giảm
Câu 2. Trong các sự kiện, hiện tượng sau, đâu là biến cố chắc chắn?
A. Mặt Trời quay quanh Trái Đất
B. Khi gieo đồng xu thì được mặt ngửa
C. Có 9 cơn bão đổ bộ vào nước ta trong năm tới
D. Ngày mai, Mặt Trời mọc ở phía Đông
Câu 3. Giá trị của biểu thức: \({x^3} - 2{x^2}\) tại \(x = - 2\) là:
A. \( - 16\)
B. \(16\)
C. \(0\)
D. \( - 8\)
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. \(4{x^2}y\left( { - 2x} \right)\)
B. \(2x\)
C. \(2xy - {x^2}\)
D. \(2021\)
Câu 5. Sắp xếp các hạng tử của đa thức \(P\left( x \right) = 2{x^3} - 7{x^2} + {x^4} - 4\) theo lũy thừa giảm dần của biến ta được:
A. \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
B. \(P\left( x \right) = 7{x^2} + 2{x^3} + {x^4} - 4\)
C. \(P\left( x \right) = - 4 - 7{x^2} + 2{x^3} + {x^4}\)
D. \(P\left( x \right) = {x^4} - 2{x^3} - 7{x^2} - 4\)
Câu 6. Cho tam giác \(MNP\) có \(NP = 1cm,MP = 7cm\). Độ dài cạnh \(MN\) là một số nguyên (cm). Độ dài cạnh \(MN\) là:
A. \(8cm\)
B. \(5cm\)
C. \(6cm\)
D. \(7cm\)
Câu 7. Cho tam giác ABC có \(AB = AC.\) Trên các cạnh AB và AC lấy các điểm D,E sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của BE và CD. Chọn câu sai.
A. \(BE = CD\)
B. \(BK = KC\)
C. \(BD = CE\)
D. \(DK = KC\)
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Một khối 7 trường THCS có 200 học sinh đăng ký thực đơn ăn trưa gồm 4 món: Pizza; mỳ Ý; Hamburger; Donut. Số phần trăm học sinh chọn Pizza là \(12,5\% \); số học sinh chọn mỳ Ý chiếm \(30\% \); số học sinh chọn bánh Hamburger chiếm một nửa tổng số học sinh khối 7. Còn lại số học sinh chọn bánh Donut.
a) Tính tỉ số phần trăm số học sinh chọn Piza và tỉ số phần trăm số học sinh chọn Donut
b) Lập bảng số liệu học sinh chọn từng loại thức ăn cho bữa trưa (đơn vị học sinh).
Bài 2. (2,5 điểm) Cho hai đa thức: \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\) và \(g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\).
a) Thu gọn và sắp xếp hai đa thức \(f\left( x \right)\) và \(g\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) và tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\).
Bài 3. (3,5 điểm) Cho tam giác ABC vuông tại A.
a) Tia phân giác của góc B cắt cạnh AC ở D. Kẻ DE vuông góc với BC tại E.
Chứng minh rằng ΔABD = ΔEBD.
b) So sánh AD và DC.
c) Tia ED cắt BA tại G. Gọi I là trung điểm GC. Chứng minh rằng B, D, I thẳng hàng.
Bài 4. (0,5 điểm) Cho \(x;{\kern 1pt} y;{\kern 1pt} z\) tỉ lệ thuận với \(3;{\kern 1pt} \,4;\,{\kern 1pt} 5.\) Tính giá trị của biểu thức
\(A = 2024\left( {x - y} \right)\left( {y - z} \right) - 506.{\left( {\dfrac{{x + y + z}}{6}} \right)^2}\)
I. Trắc nghiệm
1. C | 2. D | 3. A | 4. C |
5. A | 6. D | 7. D | 8. C |
Câu 1.
Phương pháp:
Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của số liệu trong một khoảng thời gian nhất định.
Cách giải:
Nhu cầu bán máy tính để bàn giảm mạnh trong 6 tháng,
Nhu cầu bán máy tính xách tay tăng mạnh trong 6 tháng.
Chọn C.
Câu 2.
Phương pháp:
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra
Cách giải:
Đáp án ABiến cố không thể
Đáp án BBiến cố ngẫu nhiên
Đáp án CBiến cố ngẫu nhiên
Đáp án DMặt Trời luôn mọc ở phía Đông nên sự kiện “Ngày mai, Mặt Trời mọc ở phía Đông." Luôn xảy ra nên là biến
cố chắc chắn.
Chọn D.
Câu 3.
Phương pháp:
Thay \(x = - 2\) vào biểu thức \({x^3} - 2{x^2}\) để tính.
Cách giải:
Thay \(x = - 2\) vào biểu thức \({x^3} - 2{x^2}\) ta có: \({\left( { - 2} \right)^3} - 2.{\left( { - 2} \right)^2} = \left( { - 8} \right) - 2.4 = - 16\)
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: \(2xy - {x^2}\) không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến: \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là \(a,b,c\) nếu \(\left| {b - c} \right| < a < b + c\).
+ Trong trường hợp xác định được \(a\) là số lớn nhất trong ba số \(a,b,c\) thì điều kiện tồn tại tam giác là \(a < b + c\).
Cách giải:
Xét tam giác \(MNP\), ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {NP - MP} \right| < MN < NP + MP\\ \Rightarrow \left| {1 - 7} \right| < MN < 1 + 7\\ \Rightarrow 6 < MN < 8\end{array}\)
Vì độ dài cạnh \(MN\) là một số nguyên nên \(MN = 7\,\left( {cm} \right)\)
Chọn D.
Câu 7.
Phương pháp:
Dựa vào tính chất hai tam giác bằng nhau .
Cách giải:
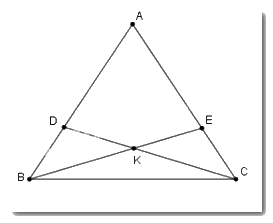
Xét tam giác ABE và tam giác ADC có
+ AD = AE (GT)
+ Góc A chung
+ AB = AC (GT)
Suy ra \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\) \( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và BE = CD (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = {180^\circ }\); \(\widehat {AEB} + \widehat {BEC} = {180^\circ }\) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
Suy ra \(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;{\mkern 1mu} AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nênC đúng.
Xét tam giác KBD và tam giác KCE có
+ \(\widehat {ABE} = \widehat {ACD}{\mkern 1mu} \left( {cmt} \right)\)
+ \(BD = EC{\mkern 1mu} \left( {cmt} \right)\)
+ \(\widehat {BDC} = \widehat {BEC}{\mkern 1mu} \left( {cmt} \right)\)
Nên \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\) \( \Rightarrow KB = KC;{\mkern 1mu} KD = KE\) (hai cạnh tương ứng) nên Bđúng, D sai.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp
a) Tổng số học sinh của trường được coi là \(100\% \), nửa tổng số học sinh là \(50\% .\)
b) Áp dụng công thức tính tỉ số phần trăm: Muốn tìm \(a\,\% \)của \(b\) ta tính \(b.\dfrac{a}{{100}}\)
Cách giải:
a) Vì số học sinh chọn bánh Hamburger chiếm một nửa tổng số học sinh khối \(7\), nên tỉ số phấn trăm số học sinh chọn bánh Hamburger là \(50\% .\)
Tỉ số phần trăm số học sinh chọn bánh Donut là: \(100\% - 12,5\% - 50\% - 30\% = 7,5\% .\)
b) Số học sinh chọn Piza là: \(200.\dfrac{{12,5}}{{100}} = 25\) (học sinh).
Số học sinh chọn Mỳ Ý là: \(200.\dfrac{{30}}{{100}} = 60\) (học sinh).
Số học sinh chọn bánh Hamburger là: \(200.\dfrac{{50}}{{100}} = 100\) (học sinh).
Số học sinh chọn bánh Donut là: \(200 - 25 - 60 - 100 = 15\) (học sinh).
Bảng số liệu: Số học sinh đăng ký thực đơn ăn trưa:
Đăng ký món | Piza | Mỳ Ý | Hambuger | Donut |
Số lượng (học sinh) | \(25\) | \(60\) | \(100\) | \(15\) |
Bài 2.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\), ta giải phương trình \(f\left( x \right) + g\left( x \right) = 0\)
Cách giải:
a) \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\)
\(\begin{array}{l}f\left( x \right) = \left( {{x^5} - {x^5}} \right) + {x^3} + \left( { - 4x + 3x} \right) + 7\\f\left( x \right) = {x^3} - x + 7\end{array}\)
\(\begin{array}{l}g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\\g\left( x \right) = - {x^3} + \left( {3{x^2} - 3{x^2}} \right) + 8x - 14\\g\left( x \right) = - {x^3} + 8x - 14\end{array}\)
b) \(f\left( x \right) + g\left( x \right) = {x^3} - x + 7 - {x^3} + 8x - 14\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^3} - x + 7 - {x^3} + 8x - 14\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x^3} - {x^3}} \right) + \left( { - x + 8x} \right) + \left( {7 - 14} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 7x - 7\end{array}\)
Ta có: \(f\left( x \right) + g\left( x \right) = 0\)
\(\begin{array}{l}7x - 7 = 0\\7x = 7\\\,\,\,x = 1\end{array}\)
Vậy \(x = 1\) là nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\)
Bài 3.
Phương pháp:
Sử dụng tính chất tia phân giác, các phương pháp chứng minh hai tam giác vuông bằng nhau, mối quan hệ giữa cạnh và góc trong tam giác, tính chất của tam giác cân.
Cách giải:
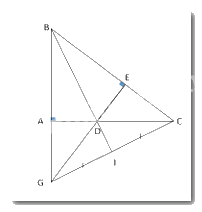
a) Chứng minh rằng ΔABD = ΔEBD.
Xét hai tam giác vuông ΔABD và ΔEBD ta có:
\(\angle A = \angle E = {90^0}\)
AD = DE (vì BD là tia phân giác)
BD cạnh chung
Suy ra ΔABD = ΔEBD (cạnh huyền – cạnh góc vuông) \( \Rightarrow \)AD = DE, BA = BE (cạnh tương ứng) (1)
b) So sánh AD và DC
Xét ΔDEC vuông tại E ta có: DC > DE
Lại có AD = DE (cmt)
\( \Rightarrow \)DC > AD
c) Chứng minh rằng B, D, I thẳng hàng.
Xét ΔBGC có AC \( \bot \) AB, GE \( \bot \) AC
Suy ra D là trực tâm của ΔBGC.(2)
Xét hai tam giác vuông ΔADG và ΔEDC ta có:
\(\angle \)ADG = \(\angle \)EDC (đối đỉnh)
\(\angle A = \angle E = \angle {90^0}\)
AD = DE (cm câu b))
Suy ra ΔADG = ΔEDC (cạnh gv – góc nhọn)
\( \Rightarrow \)AG = EC (cạnh tương ứng) (3)
từ (1), (3) suy ra BA +AG = BE + EC\( \Leftrightarrow \) BG = BC
Vậy ΔBGC là tam giác cân tại B. (4)
Từ (2), (4) suy ra BD là đường trung tuyến của tam giác ΔBGC. Hay B, D, I thẳng hàng. (đpcm)
Bài 4.
Phương pháp:
- Bước 1: Từ đề bài suy ra tỉ lệ
- Bước 2: Đặt các tỉ lệ bằng \(k\) từ đó suy ra \(x,{\kern 1pt} y,{\kern 1pt} z\) theo \(k\)
- Bước 3: Thay vào đề bài và tính toán
- Bước 4: Kết luận
Cách giải:
Vì \(x;\,{\kern 1pt} y;{\kern 1pt} \,z\) tỉ lệ thuận với \(3;{\kern 1pt} \,\,4;\,\,{\kern 1pt} 5\) \( \Rightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}\). Đặt \(\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3k}\\{y = 4k}\\{z = 5k}\end{array}} \right.\). Khi đó,\(A = 2024\left( {3k - 4k} \right)\left( {4k - 5k} \right) - 506.{\left( {\dfrac{{3k + 4k + 5k}}{6}} \right)^2}\)
\(A = 2024\left( { - k} \right)\left( { - k} \right) - 506.{\left( {2k} \right)^2}\)
\(A = 2024.{k^2} - 506.4.{k^2}\)
\(A = 2024{k^2} - 2024{k^2}\)
\(A = 0\)
Vậy \(A = 0.\)
Kỳ thi học kì 2 Toán 7 là một bước quan trọng trong quá trình học tập của các em học sinh. Để giúp các em chuẩn bị tốt nhất, Giaitoan.edu.vn xin giới thiệu chi tiết Đề thi học kì 2 Toán 7 - Đề số 4 - Cánh diều, kèm theo hướng dẫn giải chi tiết và dễ hiểu.
Đề thi này bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã học trong học kì 2 như:
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể. Các bài toán được thiết kế với độ khó tăng dần, từ dễ đến khó, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề.
Giaitoan.edu.vn cung cấp hướng dẫn giải chi tiết cho từng câu hỏi trong đề thi, giúp học sinh hiểu rõ phương pháp giải và cách tiếp cận bài toán. Các bước giải được trình bày rõ ràng, dễ hiểu, kèm theo các chú thích và giải thích cần thiết.
Câu 1: (Trắc nghiệm) Giá trị của biểu thức 3x + 5 tại x = -2 là:
Giải: Thay x = -2 vào biểu thức 3x + 5, ta được: 3*(-2) + 5 = -6 + 5 = -1. Vậy đáp án đúng là -1.
Câu 2: (Tự luận) Giải phương trình: 2x - 3 = 7
Giải:
Vậy nghiệm của phương trình là x = 5.
Ngoài Đề thi học kì 2 Toán 7 - Đề số 4 - Cánh diều, Giaitoan.edu.vn còn cung cấp nhiều đề thi khác với các mức độ khó khác nhau, giúp học sinh có thêm nhiều cơ hội luyện tập và nâng cao kiến thức. Hãy truy cập Giaitoan.edu.vn để khám phá thêm!
Để hỗ trợ học sinh ôn thi hiệu quả hơn, Giaitoan.edu.vn còn cung cấp các tài liệu ôn thi bổ trợ như:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao!