Chào mừng bạn đến với bộ đề trắc nghiệm Toán 7 Bài 11: Định lí và chứng minh định lí, chương trình Kết nối tri thức. Bài tập này được thiết kế để giúp các em học sinh ôn luyện và củng cố kiến thức về định lí, cách chứng minh định lí và ứng dụng trong giải toán.
Giaitoan.edu.vn cung cấp đầy đủ các dạng bài tập trắc nghiệm, từ cơ bản đến nâng cao, giúp các em tự tin làm bài kiểm tra và đạt kết quả tốt nhất.
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Cho định lý: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
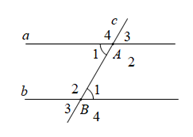
\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
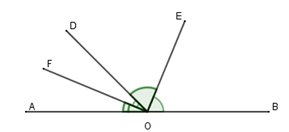
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
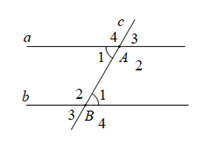
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Phát biểu định lý sau bằng lời:
GT | \(a \bot c;b \bot c\) |
KL | \(a//c\) |
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Định lý sau được phát biểu thành lời là:
GT | \(a//b;c \bot a\) |
KL | \(c \bot b\) |
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Chọn khẳng định đúng:
Tia phân giác của 2 góc đối đỉnh trùng nhau
2 tia phân giác của 2 góc phụ nhau thì vuông góc với nhau
Hai góc bằng nhau thì đối đỉnh.
2 tia phân giác của 2 góc đối đỉnh là 2 cạnh của 1 góc bẹt.
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Lời giải và đáp án
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng định nghĩa “chứng minh định lý”.
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Đáp án : D
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
+ “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.”
+ “Hai góc đối đỉnh thì bằng nhau”
Câu D không là định lí vì khẳng định D sai
Cho định lý: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
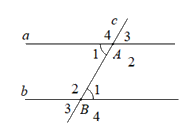
\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Đáp án : B
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
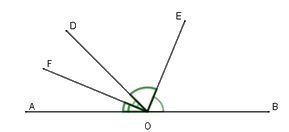
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
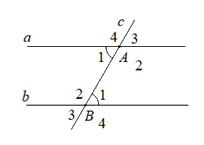
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Đáp án : B
Xét vị trí của góc A1 so với góc B1 rồi xét giả thiết của từng định lý
Đường thẳng c cắt đường thẳng a và b, tạo thành cặp góc so le trong bằng nhau (\(\widehat {{A_1}} = \widehat {{B_1}}\)) thì a // b
Vậy định lý là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song”
Phát biểu định lý sau bằng lời:
GT | \(a \bot c;b \bot c\) |
KL | \(a//c\) |
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Đáp án : C
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Định lý sau được phát biểu thành lời là:
GT | \(a//b;c \bot a\) |
KL | \(c \bot b\) |
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Đáp án : D
Lý thuyết về định lí
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Chọn khẳng định đúng:
Tia phân giác của 2 góc đối đỉnh trùng nhau
2 tia phân giác của 2 góc phụ nhau thì vuông góc với nhau
Hai góc bằng nhau thì đối đỉnh.
2 tia phân giác của 2 góc đối đỉnh là 2 cạnh của 1 góc bẹt.
Đáp án : D
Xét tính đúng, sai của từng khẳng định
+ Tia phân giác của 2 góc đối đỉnh là đối nhau nên A sai
+ 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau nên B sai
+ 2 góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau chưa chắc đã đối đỉnh nên C sai
+ 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau nên là 2 cạnh của 1 góc bẹt. Do đó D đúng.
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Đáp án : A
Lý thuyết về định lí
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …”
Các khẳng định B,C,D đúng .
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Đáp án : A
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Cho định lý: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
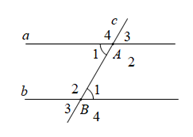
\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:

Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
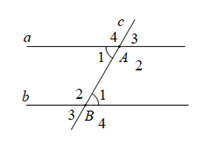
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Phát biểu định lý sau bằng lời:
GT | \(a \bot c;b \bot c\) |
KL | \(a//c\) |
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Định lý sau được phát biểu thành lời là:
GT | \(a//b;c \bot a\) |
KL | \(c \bot b\) |
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Chọn khẳng định đúng:
Tia phân giác của 2 góc đối đỉnh trùng nhau
2 tia phân giác của 2 góc phụ nhau thì vuông góc với nhau
Hai góc bằng nhau thì đối đỉnh.
2 tia phân giác của 2 góc đối đỉnh là 2 cạnh của 1 góc bẹt.
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng định nghĩa “chứng minh định lý”.
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Đáp án : D
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
+ “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.”
+ “Hai góc đối đỉnh thì bằng nhau”
Câu D không là định lí vì khẳng định D sai
Cho định lý: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
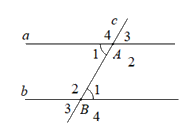
\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Đáp án : B
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:

Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
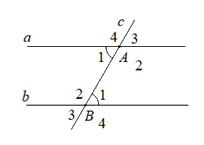
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Đáp án : B
Xét vị trí của góc A1 so với góc B1 rồi xét giả thiết của từng định lý
Đường thẳng c cắt đường thẳng a và b, tạo thành cặp góc so le trong bằng nhau (\(\widehat {{A_1}} = \widehat {{B_1}}\)) thì a // b
Vậy định lý là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song”
Phát biểu định lý sau bằng lời:
GT | \(a \bot c;b \bot c\) |
KL | \(a//c\) |
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Đáp án : C
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Định lý sau được phát biểu thành lời là:
GT | \(a//b;c \bot a\) |
KL | \(c \bot b\) |
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Đáp án : D
Lý thuyết về định lí
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Chọn khẳng định đúng:
Tia phân giác của 2 góc đối đỉnh trùng nhau
2 tia phân giác của 2 góc phụ nhau thì vuông góc với nhau
Hai góc bằng nhau thì đối đỉnh.
2 tia phân giác của 2 góc đối đỉnh là 2 cạnh của 1 góc bẹt.
Đáp án : D
Xét tính đúng, sai của từng khẳng định
+ Tia phân giác của 2 góc đối đỉnh là đối nhau nên A sai
+ 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau nên B sai
+ 2 góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau chưa chắc đã đối đỉnh nên C sai
+ 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau nên là 2 cạnh của 1 góc bẹt. Do đó D đúng.
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Đáp án : A
Lý thuyết về định lí
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …”
Các khẳng định B,C,D đúng .
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Đáp án : A
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Bài 11 trong chương trình Toán 7 Kết nối tri thức tập trung vào việc giới thiệu khái niệm định lí, các thành phần của một định lí (giả thiết, kết luận) và phương pháp chứng minh định lí. Đây là nền tảng quan trọng cho việc học toán ở các lớp trên, giúp học sinh phát triển tư duy logic và khả năng lập luận.
Một định lí là một khẳng định đúng được chứng minh bằng lập luận logic. Một định lí thường có cấu trúc:
Ví dụ: Nếu a và b là hai số tự nhiên chẵn thì a + b là một số chẵn.
Chứng minh định lí là quá trình sử dụng các định lí, tính chất đã biết và các phép suy luận logic để chứng minh rằng kết luận của định lí là đúng khi giả thiết đúng.
Các bước chứng minh định lí thường bao gồm:
Dạng bài tập này yêu cầu học sinh xác định đúng định lí, giả thiết và kết luận trong một câu khẳng định cho trước.
Ví dụ: Trong câu “Nếu hai góc đối đỉnh thì bằng nhau”, giả thiết là gì? Kết luận là gì?
Dạng bài tập này yêu cầu học sinh sử dụng các định lí đã học để giải các bài toán cụ thể.
Ví dụ: Cho tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tính góc C.
Dạng bài tập này yêu cầu học sinh tự chứng minh một số định lí đơn giản bằng cách sử dụng các định lí, tính chất đã biết.
Ví dụ: Chứng minh rằng hai đường thẳng song song thì không có điểm chung.
Để nắm vững kiến thức về định lí và chứng minh định lí, các em nên luyện tập thêm với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho đề trắc nghiệm phong phú, đa dạng, giúp các em ôn luyện và củng cố kiến thức một cách hiệu quả.
Bài 11: Định lí và chứng minh định lí Toán 7 Kết nối tri thức là một bài học quan trọng, giúp học sinh phát triển tư duy logic và khả năng lập luận. Hy vọng với bộ đề trắc nghiệm này, các em sẽ tự tin hơn trong việc học tập và đạt kết quả tốt nhất.