Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh lớp 7 ôn luyện và kiểm tra kiến thức về quan hệ giữa ba cạnh trong một tam giác, thuộc chương trình Toán 7 Kết nối tri thức.
Các câu hỏi được thiết kế đa dạng, bao gồm nhiều dạng bài tập khác nhau, có đáp án chi tiết để học sinh tự đánh giá kết quả học tập.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán.
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
\(AB + BC > AC\)
\(BC - AB < AC\)
\(BC - AB < AC < BC + AB\)
\(AB - AC > BC\).
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
$3cm,5cm,7cm$
$4cm,5cm,6cm$
$2cm,5cm,7cm$
$3cm,6cm,5cm.$
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
$2cm$
$3cm$
$4cm$
$6cm.$
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
$17\,cm$
$15\,cm$
$13\,cm$
$16\,cm.$
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
\(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
\(BC = 7\,cm\)
\(BC = 5\,cm.\)
$BC = 6\,cm.$
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
\(AB + AC < 2AM\)
\(AB + AC > 2AM\)
\(AB + AC = 2AM\)
\(AB + AC \le 2AM\).
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
\(OA + OC < BA + BC\)
\(OA + OC > BA + BC\)
\(OA + OC = BA + BC\)
\(OA + OC \ge BA + BC\).
Cho hình vẽ dưới đây. Chọn câu đúng.
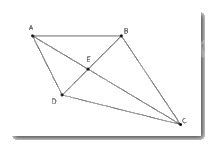
$AB + BC + CD + DA < AC + BD$
$AB + BC + CD + DA < 2\left( {AC + BD} \right)$
$AB + BC + CD + DA > 2\left( {AC + BD} \right)$
$AB + BC + CD + DA = 2\left( {AC + BD} \right)$
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
\(AD\) bằng nửa chu vi của tam giác \(ABC\).
\(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
\(AD\) lớn hơn chu vi của tam giác \(ABC\).
\(AD\) lớn hơn nửa chu vi của tam giác \(ABC\).
Lời giải và đáp án
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
\(AB + BC > AC\)
\(BC - AB < AC\)
\(BC - AB < AC < BC + AB\)
\(AB - AC > BC\).
Đáp án : D
Áp dụng bất đẳng thức tam giác.
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đều đúng, đáp án D sai.
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
$3cm,5cm,7cm$
$4cm,5cm,6cm$
$2cm,5cm,7cm$
$3cm,6cm,5cm.$
Đáp án : C
Ta kiểm tra tổng độ dài 2 đoạn thẳng ngắn hơn có lớn hơn độ dài đoạn thẳng dài nhất hay không. Nếu thỏa mãn thì 3 đoạn thẳng đã cho ghép được thành 1 tam giác.
+ Xét bộ ba: $3cm,5cm,7cm.$ Ta có: \(3 + 5 = 8 > 7\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,7cm$ lập thành một tam giác. Loại đáp án A.
+ Xét bộ ba: $4cm,5cm,6cm$. Ta có: \(4 + 5 = 9 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $4cm,5cm,6cm$ lập thành một tam giác. Loại đáp án B.
+ Xét bộ ba: $2cm,5cm,7cm.$ Ta có: \(2 + 5 = 7\) (không thỏa mãn bất đẳng thức tam giác) nên bộ ba $2cm,5cm,7cm$ không lập thành một tam giác. Chọn đáp án C.
+ Xét bộ ba: $3cm,5cm,6cm.$ Ta có: \(3 + 5 = 8 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,6cm$ lập thành một tam giác. Loại đáp án D.
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
$2cm$
$3cm$
$4cm$
$6cm.$
Đáp án : D
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh CA là số nguyên chẵn
Theo bất đẳng thức tam giác ta có:
\(6 - 2 < AC< 6 + 2 \)
\(4 < AC < 8\).
Vì độ dài $AC$ là số tự nhiên chẵn nên $AC = 6cm.$
Vậy độ dài cạnh $AC = 6cm.$
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
$17\,cm$
$15\,cm$
$13\,cm$
$16\,cm.$
Đáp án : C
Áp dụng bất đẳng thức trong tam giác để tính cạnh \(AC.\)
Từ đó tính chu vi tam giác \(ABC.\)
Gọi độ dài cạnh $AC$ là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(6 - 1 < x < 6 + 1 \Leftrightarrow 5 < x < 7\). Vì $x$ là số nguyên nên $x = 6.$ Độ dài cạnh $AC = 6cm.$
Chu vi tam giác \(ABC\) là \(AB + BC + AC = 1 + 6 + 6 = 13\,cm.\)
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
\(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
\(BC = 7\,cm\)
\(BC = 5\,cm.\)
$BC = 6\,cm.$
Đáp án : A
- Áp dụng tính chất tam giác cân.
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
Giả sử \(\Delta ABC\) cân tại $A.$
- Trường hợp 1:
\(AB = AC = 5cm \) thì \( BC = 17 - 5 - 5 = 7cm.\)
Ta có: \(AB + AC = 5 + 5 = 10 > BC = 7cm\) (thỏa mãn bất đẳng thức tam giác)
- Trường hợp 2: \(BC = 5cm \) thì \(AB = AC = \left( {17 - 5} \right):2 = 6cm\)
Ta có: \(AB + BC = 5 + 6 = 11 > AC = 6cm\) (thỏa mãn bất đẳng thức tam giác)
Vậy nếu \(\Delta ABC\) cân tại A có:
+ \(AB = AC = 5cm \) thì \(BC = 7cm\)
+ \(BC = 5cm \) thì \(AB = AC = 6cm\)
Vậy \(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
\(AB + AC < 2AM\)
\(AB + AC > 2AM\)
\(AB + AC = 2AM\)
\(AB + AC \le 2AM\).
Đáp án : B
- Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
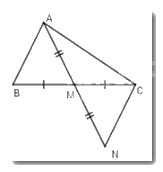
Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$
Vì $M$ là trung điểm của $BC$ (gt) \( \Rightarrow MB = MC\) (tính chất trung điểm)
Xét \(\Delta MAB\) và \(\Delta MNC\) có:
\(MB = MC\left( {cmt} \right)\)
\(\widehat {AMB} = \widehat {NMC}\) (đối đỉnh)
\(AM = MN\left( {gt} \right)\)
\( \Rightarrow \Delta MAB = \Delta MNC\left( {c - g - c} \right)\) \( \Rightarrow NC = AB\left( 1 \right)\) (2 cạnh tương ứng)
Xét \(\Delta ACN\) có: \(AN < AC + CN\left( 2 \right)\) (bất đẳng thức tam giác)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow AN < AC + AB\).
Mặt khác, \(AN = 2AM\left( {gt} \right) \Rightarrow 2AM < AB + AC.\)
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
\(OA + OC < BA + BC\)
\(OA + OC > BA + BC\)
\(OA + OC = BA + BC\)
\(OA + OC \ge BA + BC\).
Đáp án : A
- Gọi giao điểm của $AO$ và $BC$ là $D.$
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
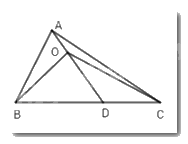
Gọi giao điểm của $AO$ và $BC$ là $D.$ Do $O$ nằm trong \(\Delta ABC\) nên $D$ nằm giữa $B$ và $C$\( \Rightarrow BC = BD + DC\left( * \right)\)
Xét \(\Delta ABD\) có: \(AD < AB + BD\) (bất đẳng thức tam giác)
\( \Rightarrow OA + OD < AB + BD\left( 1 \right)\)
Xét \(\Delta OCD\) có: \(OC < OD + DC\left( 2 \right)\) (bất đẳng thức tam giác)
Cộng vế với vế của \(\left( 1 \right)\) và \(\left( 2 \right)\) ta được:
\(OA + OD + OC < AB + BD + OD + DC\) \( \Rightarrow OA + OC < AB + BD + DC\left( {**} \right)\)
Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta có: \(OA + OC < AB + BC.\)
Cho hình vẽ dưới đây. Chọn câu đúng.
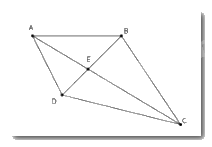
$AB + BC + CD + DA < AC + BD$
$AB + BC + CD + DA < 2\left( {AC + BD} \right)$
$AB + BC + CD + DA > 2\left( {AC + BD} \right)$
$AB + BC + CD + DA = 2\left( {AC + BD} \right)$
Đáp án : B
Sử dụng quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh kia.
Áp dụng quan hệ giữa ba cạnh của một tam giác:
Xét tam giác \(AED\) có \(AE + ED > AD\,\,\,\left( 1 \right)\)
Xét tam giác \(ECD\) có \(CE + DE > CD\,\,\left( 2 \right)\)
Xét tam giác \(EBC\) có \(EB + EC > BC\,\left( 3 \right)\)
Xét tam giác \(ABE\) có \(AE + EB > AB\,\,\,\left( 4 \right)\)
Từ \(\left( 1 \right);\left( 2 \right);\left( 3 \right);\left( 4 \right)\) ta có \(AE + DE + CE + DE + BE + CE + AE + BE > AD + CD + BC + AB\)
Mà \(AE + EC = AC;\,DE + BE = BD\) nên \(2\left( {AC + BD} \right) > AB + BC + CD + DA\) .
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
\(AD\) bằng nửa chu vi của tam giác \(ABC\).
\(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
\(AD\) lớn hơn chu vi của tam giác \(ABC\).
\(AD\) lớn hơn nửa chu vi của tam giác \(ABC\).
Đáp án : B
- Nối đoạn thẳng AD.
- Áp dụng bất đẳng thức tam giác chứng minh: \(AD < AC + CD\), \(AD < AB + DB\). Từ đó lập luận suy ra điều phải chứng minh.
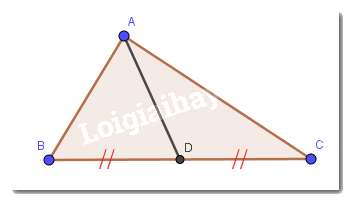
Nối đoạn thẳng AD.
Xét \(\Delta ADC\) có: \(AD < AC + CD\) (bất đẳng thức tam giác) (1)
Xét \(\Delta ADB\) có: \(AD < AB + DB\) (bất đẳng thức tam giác) (2)
Vì \(D\) là trung điểm của \(BC\) (gt) nên \(D\) nằm giữa \(B\) và \(C\) ta có: \(CD + DB = BC.\)
Cộng vế với vế của (1) và (2), ta được:
\(\begin{array}{l}AD + AD < AC + CD + AB + DB\\ \Rightarrow 2AD < AB + \left( {CD + DB} \right) + AC\\ \Rightarrow 2AD < AB + BC + AC\\ \Rightarrow AD < \dfrac{{AB + BC + AC}}{2}\end{array}\)
Do đó \(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
\(AB + BC > AC\)
\(BC - AB < AC\)
\(BC - AB < AC < BC + AB\)
\(AB - AC > BC\).
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
$3cm,5cm,7cm$
$4cm,5cm,6cm$
$2cm,5cm,7cm$
$3cm,6cm,5cm.$
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
$2cm$
$3cm$
$4cm$
$6cm.$
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
$17\,cm$
$15\,cm$
$13\,cm$
$16\,cm.$
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
\(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
\(BC = 7\,cm\)
\(BC = 5\,cm.\)
$BC = 6\,cm.$
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
\(AB + AC < 2AM\)
\(AB + AC > 2AM\)
\(AB + AC = 2AM\)
\(AB + AC \le 2AM\).
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
\(OA + OC < BA + BC\)
\(OA + OC > BA + BC\)
\(OA + OC = BA + BC\)
\(OA + OC \ge BA + BC\).
Cho hình vẽ dưới đây. Chọn câu đúng.

$AB + BC + CD + DA < AC + BD$
$AB + BC + CD + DA < 2\left( {AC + BD} \right)$
$AB + BC + CD + DA > 2\left( {AC + BD} \right)$
$AB + BC + CD + DA = 2\left( {AC + BD} \right)$
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
\(AD\) bằng nửa chu vi của tam giác \(ABC\).
\(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
\(AD\) lớn hơn chu vi của tam giác \(ABC\).
\(AD\) lớn hơn nửa chu vi của tam giác \(ABC\).
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
\(AB + BC > AC\)
\(BC - AB < AC\)
\(BC - AB < AC < BC + AB\)
\(AB - AC > BC\).
Đáp án : D
Áp dụng bất đẳng thức tam giác.
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đều đúng, đáp án D sai.
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
$3cm,5cm,7cm$
$4cm,5cm,6cm$
$2cm,5cm,7cm$
$3cm,6cm,5cm.$
Đáp án : C
Ta kiểm tra tổng độ dài 2 đoạn thẳng ngắn hơn có lớn hơn độ dài đoạn thẳng dài nhất hay không. Nếu thỏa mãn thì 3 đoạn thẳng đã cho ghép được thành 1 tam giác.
+ Xét bộ ba: $3cm,5cm,7cm.$ Ta có: \(3 + 5 = 8 > 7\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,7cm$ lập thành một tam giác. Loại đáp án A.
+ Xét bộ ba: $4cm,5cm,6cm$. Ta có: \(4 + 5 = 9 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $4cm,5cm,6cm$ lập thành một tam giác. Loại đáp án B.
+ Xét bộ ba: $2cm,5cm,7cm.$ Ta có: \(2 + 5 = 7\) (không thỏa mãn bất đẳng thức tam giác) nên bộ ba $2cm,5cm,7cm$ không lập thành một tam giác. Chọn đáp án C.
+ Xét bộ ba: $3cm,5cm,6cm.$ Ta có: \(3 + 5 = 8 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,6cm$ lập thành một tam giác. Loại đáp án D.
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
$2cm$
$3cm$
$4cm$
$6cm.$
Đáp án : D
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh CA là số nguyên chẵn
Theo bất đẳng thức tam giác ta có:
\(6 - 2 < AC< 6 + 2 \)
\(4 < AC < 8\).
Vì độ dài $AC$ là số tự nhiên chẵn nên $AC = 6cm.$
Vậy độ dài cạnh $AC = 6cm.$
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
$17\,cm$
$15\,cm$
$13\,cm$
$16\,cm.$
Đáp án : C
Áp dụng bất đẳng thức trong tam giác để tính cạnh \(AC.\)
Từ đó tính chu vi tam giác \(ABC.\)
Gọi độ dài cạnh $AC$ là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(6 - 1 < x < 6 + 1 \Leftrightarrow 5 < x < 7\). Vì $x$ là số nguyên nên $x = 6.$ Độ dài cạnh $AC = 6cm.$
Chu vi tam giác \(ABC\) là \(AB + BC + AC = 1 + 6 + 6 = 13\,cm.\)
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
\(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
\(BC = 7\,cm\)
\(BC = 5\,cm.\)
$BC = 6\,cm.$
Đáp án : A
- Áp dụng tính chất tam giác cân.
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
Giả sử \(\Delta ABC\) cân tại $A.$
- Trường hợp 1:
\(AB = AC = 5cm \) thì \( BC = 17 - 5 - 5 = 7cm.\)
Ta có: \(AB + AC = 5 + 5 = 10 > BC = 7cm\) (thỏa mãn bất đẳng thức tam giác)
- Trường hợp 2: \(BC = 5cm \) thì \(AB = AC = \left( {17 - 5} \right):2 = 6cm\)
Ta có: \(AB + BC = 5 + 6 = 11 > AC = 6cm\) (thỏa mãn bất đẳng thức tam giác)
Vậy nếu \(\Delta ABC\) cân tại A có:
+ \(AB = AC = 5cm \) thì \(BC = 7cm\)
+ \(BC = 5cm \) thì \(AB = AC = 6cm\)
Vậy \(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
\(AB + AC < 2AM\)
\(AB + AC > 2AM\)
\(AB + AC = 2AM\)
\(AB + AC \le 2AM\).
Đáp án : B
- Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$
Vì $M$ là trung điểm của $BC$ (gt) \( \Rightarrow MB = MC\) (tính chất trung điểm)
Xét \(\Delta MAB\) và \(\Delta MNC\) có:
\(MB = MC\left( {cmt} \right)\)
\(\widehat {AMB} = \widehat {NMC}\) (đối đỉnh)
\(AM = MN\left( {gt} \right)\)
\( \Rightarrow \Delta MAB = \Delta MNC\left( {c - g - c} \right)\) \( \Rightarrow NC = AB\left( 1 \right)\) (2 cạnh tương ứng)
Xét \(\Delta ACN\) có: \(AN < AC + CN\left( 2 \right)\) (bất đẳng thức tam giác)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow AN < AC + AB\).
Mặt khác, \(AN = 2AM\left( {gt} \right) \Rightarrow 2AM < AB + AC.\)
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
\(OA + OC < BA + BC\)
\(OA + OC > BA + BC\)
\(OA + OC = BA + BC\)
\(OA + OC \ge BA + BC\).
Đáp án : A
- Gọi giao điểm của $AO$ và $BC$ là $D.$
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Gọi giao điểm của $AO$ và $BC$ là $D.$ Do $O$ nằm trong \(\Delta ABC\) nên $D$ nằm giữa $B$ và $C$\( \Rightarrow BC = BD + DC\left( * \right)\)
Xét \(\Delta ABD\) có: \(AD < AB + BD\) (bất đẳng thức tam giác)
\( \Rightarrow OA + OD < AB + BD\left( 1 \right)\)
Xét \(\Delta OCD\) có: \(OC < OD + DC\left( 2 \right)\) (bất đẳng thức tam giác)
Cộng vế với vế của \(\left( 1 \right)\) và \(\left( 2 \right)\) ta được:
\(OA + OD + OC < AB + BD + OD + DC\) \( \Rightarrow OA + OC < AB + BD + DC\left( {**} \right)\)
Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta có: \(OA + OC < AB + BC.\)
Cho hình vẽ dưới đây. Chọn câu đúng.

$AB + BC + CD + DA < AC + BD$
$AB + BC + CD + DA < 2\left( {AC + BD} \right)$
$AB + BC + CD + DA > 2\left( {AC + BD} \right)$
$AB + BC + CD + DA = 2\left( {AC + BD} \right)$
Đáp án : B
Sử dụng quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh kia.
Áp dụng quan hệ giữa ba cạnh của một tam giác:
Xét tam giác \(AED\) có \(AE + ED > AD\,\,\,\left( 1 \right)\)
Xét tam giác \(ECD\) có \(CE + DE > CD\,\,\left( 2 \right)\)
Xét tam giác \(EBC\) có \(EB + EC > BC\,\left( 3 \right)\)
Xét tam giác \(ABE\) có \(AE + EB > AB\,\,\,\left( 4 \right)\)
Từ \(\left( 1 \right);\left( 2 \right);\left( 3 \right);\left( 4 \right)\) ta có \(AE + DE + CE + DE + BE + CE + AE + BE > AD + CD + BC + AB\)
Mà \(AE + EC = AC;\,DE + BE = BD\) nên \(2\left( {AC + BD} \right) > AB + BC + CD + DA\) .
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
\(AD\) bằng nửa chu vi của tam giác \(ABC\).
\(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
\(AD\) lớn hơn chu vi của tam giác \(ABC\).
\(AD\) lớn hơn nửa chu vi của tam giác \(ABC\).
Đáp án : B
- Nối đoạn thẳng AD.
- Áp dụng bất đẳng thức tam giác chứng minh: \(AD < AC + CD\), \(AD < AB + DB\). Từ đó lập luận suy ra điều phải chứng minh.

Nối đoạn thẳng AD.
Xét \(\Delta ADC\) có: \(AD < AC + CD\) (bất đẳng thức tam giác) (1)
Xét \(\Delta ADB\) có: \(AD < AB + DB\) (bất đẳng thức tam giác) (2)
Vì \(D\) là trung điểm của \(BC\) (gt) nên \(D\) nằm giữa \(B\) và \(C\) ta có: \(CD + DB = BC.\)
Cộng vế với vế của (1) và (2), ta được:
\(\begin{array}{l}AD + AD < AC + CD + AB + DB\\ \Rightarrow 2AD < AB + \left( {CD + DB} \right) + AC\\ \Rightarrow 2AD < AB + BC + AC\\ \Rightarrow AD < \dfrac{{AB + BC + AC}}{2}\end{array}\)
Do đó \(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
Trong hình học, việc hiểu rõ mối quan hệ giữa các cạnh của một tam giác là nền tảng quan trọng để giải quyết nhiều bài toán. Bài 33 trong chương trình Toán 7 Kết nối tri thức tập trung vào việc khám phá và áp dụng các bất đẳng thức tam giác, giúp học sinh nắm vững các quy tắc cơ bản về độ dài cạnh trong một tam giác.
Bất đẳng thức tam giác là một trong những khái niệm cốt lõi của bài học này. Nó khẳng định rằng:
Ví dụ, nếu tam giác ABC có các cạnh a, b, c thì:
Việc hiểu rõ bất đẳng thức tam giác giúp chúng ta kiểm tra xem ba đoạn thẳng có thể tạo thành một tam giác hay không.
Bất đẳng thức tam giác có nhiều ứng dụng trong thực tế và trong các bài toán hình học. Một số ứng dụng phổ biến bao gồm:
Trong các bài kiểm tra và bài tập về Bài 33, học sinh thường gặp các dạng bài sau:
Để giải các bài tập về Bài 33, học sinh cần:
Khi gặp một bài toán, hãy xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, áp dụng bất đẳng thức tam giác để tìm ra lời giải.
Ví dụ 1: Cho tam giác ABC có AB = 3cm, BC = 4cm, AC = 5cm. Chứng minh rằng tam giác ABC là tam giác vuông.
Giải: Ta có: AB2 + BC2 = 32 + 42 = 9 + 16 = 25 = 52 = AC2. Vậy, theo định lý Pytago đảo, tam giác ABC là tam giác vuông tại B.
Để củng cố kiến thức về Bài 33, học sinh nên:
Bài 33: Quan hệ giữa ba cạnh trong một tam giác là một bài học quan trọng trong chương trình Toán 7. Việc nắm vững các khái niệm và ứng dụng của bất đẳng thức tam giác sẽ giúp học sinh giải quyết nhiều bài toán hình học một cách hiệu quả. Giaitoan.edu.vn hy vọng rằng với bộ câu hỏi trắc nghiệm và hướng dẫn giải chi tiết này, học sinh sẽ có thêm công cụ để học tập và ôn luyện môn Toán.