Chào mừng bạn đến với bài trắc nghiệm trực tuyến về Bài 28: Phép chia đa thức một biến, chương trình Toán 7 Kết nối tri thức. Bài trắc nghiệm này được thiết kế để giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Với hình thức trắc nghiệm, bạn sẽ được kiểm tra nhanh chóng và hiệu quả khả năng hiểu và vận dụng các kiến thức về phép chia đa thức một biến.
Tìm kết quả của phép chia 8x4 - 2x3 cho 4x2
2x2
4x5
2x2 - 0,5.x
2x2 + 1
Phép chia 2x4 – x3 + 2x – 1 cho x2 – x + 1 có thương là:
0,5. x2 + 2x – 1
- 2x2 + 2x – 1
2x2 + x – 1
2x2 + x + 1
Phép chia 2x5 – 3x3 + 1 cho -2x3 + 3 có dư là:
3x2 – 3,5
–x2 + 1,5
x2 - 1,5
-3x2 + 3,5
Thương của phép chia đa thức một biến bậc 6 cho đa thức một biến bậc 2 là đa thức bậc mấy?
2
3
4
Không xác định được
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
\({x^3} + 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} - 5x + 1\)
\({x^3} + 4{x^2} - 5x + 1\)
Tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 2\)
\(8\)
\(9\)
\(10\)
\(12\)
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
\(a = 0\) và \(b = - 16\)
\(a = 0\) và \(b = 16\)
\(a = 0\) và \(b = 0\)
\(a = 1\) và \(b = 1\)
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\):
\( - 4\)
\(2\)
\( - 2\)
\(4\)
Cho \(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Có bao nhiêu giá trị \(n \in Z\) để \(P \in Z\).
0
1
2
Vô số
Lời giải và đáp án
Tìm kết quả của phép chia 8x4 - 2x3 cho 4x2
2x2
4x5
2x2 - 0,5.x
2x2 + 1
Đáp án : C
Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
Ta có:
(8x4 - 2x3) : 4x2 = 8x4 : 4x2 - 2x3 : 4x2 = 2x2 – 0,5.x
Phép chia 2x4 – x3 + 2x – 1 cho x2 – x + 1 có thương là:
0,5. x2 + 2x – 1
- 2x2 + 2x – 1
2x2 + x – 1
2x2 + x + 1
Đáp án : C
Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
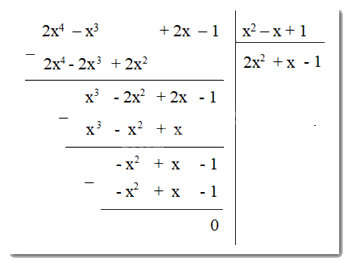
Phép chia 2x5 – 3x3 + 1 cho -2x3 + 3 có dư là:
3x2 – 3,5
–x2 + 1,5
x2 - 1,5
-3x2 + 3,5
Đáp án : A
Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
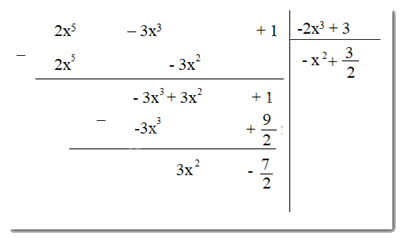
Vậy số dư là \(3x^2 - \frac{7}{2} = 3x^2 – 3,5\)
Thương của phép chia đa thức một biến bậc 6 cho đa thức một biến bậc 2 là đa thức bậc mấy?
2
3
4
Không xác định được
Đáp án : C
Viết dạng tổng quát của phép chia đa thức bậc 6 cho đa thức bậc 2
Ta có: Đa thức biến x bậc 6 có dạng: a6 . x6 + a5 . x5 + a4 . x4 + a3 . x3 + a2 . x2 + a1. x + a0 (a6 khác 0)
Đa thức biến x bậc 2 có dạng: b2 . x2 + b1. x + b0 (b2 khác 0)
Khi chia đa thức biến x bậc 6 cho đa thức biến x bậc 2, đầu tiên, ta lấy hạng tử : a6 . x6 chia cho b2 . x2 nên thu được đa thức thương có bậc là 6 – 2 = 4
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
\({x^3} + 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} - 5x + 1\)
\({x^3} + 4{x^2} - 5x + 1\)
Đáp án : A
Tìm đa thức A thỏa mãn A = B. Q + R
Trong đó, A là đa thức bị chia, B là đa thức chia, Q là thương, R là dư
Ta có: Đa thức bị chia = \(\left( {{x^2} + x + 1} \right)\). \(\left( {x + 3} \right)\) + \(x - 2\)
= x2 . (x + 3) + x. (x+3) + 1. (x+3) + x – 2
= x2 . x + x2 . 3 + x .x + x . 3 + 1. x + 1.3 + x – 2
= x3 + 3x2 + x2 + 3x + x + 3 + x – 2
= x3 + (3x2 + x2 ) + (3x + x + x ) + (3 – 2)
= x3 + 4x2 + 5x + 1
Tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 2\)
\(8\)
\(9\)
\(10\)
\(12\)
Đáp án : A
+) Chia đa thức cho đa thức: Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Thay x = 2 vào đa thức thương vừa thu được
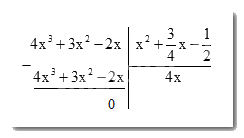
Tại \(x = 2\) , ta có: \(A = 4x = 4.2 = 8\)
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
\(a = 0\) và \(b = - 16\)
\(a = 0\) và \(b = 16\)
\(a = 0\) và \(b = 0\)
\(a = 1\) và \(b = 1\)
Đáp án : A
+) Chia đa thức cho đa thức: Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Biện luận để \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\) thì dư = 0, tìm a,b
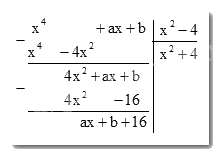
Để \({x^4} + ax + b\) chia hết cho \({x^2} - 4\) thì
\(ax + b + 16 = 0 \)
\(ax = 0\) và \(b + 16 = 0\)
suy ra \(a = 0\) và \(b = - 16\)
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\):
\( - 4\)
\(2\)
\( - 2\)
\(4\)
Đáp án : D
+) Chia đa thức cho đa thức: Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Biện luận để dư = 2
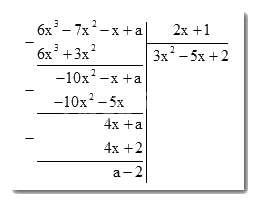
Để \(6{x^3} - 7{x^2} - x + a\) chia \(2x + 1\) dư \(2\) thì \(a - 2 = 2 \Leftrightarrow a = 4\).
Cho \(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Có bao nhiêu giá trị \(n \in Z\) để \(P \in Z\).
0
1
2
Vô số
Đáp án : C
- Đặt phép chia.
- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia nên số chia là ước của số dư cuối cùng.
- Lập bảng thử chọn để chọn ra giá trị của \(n\)thỏa mãn.
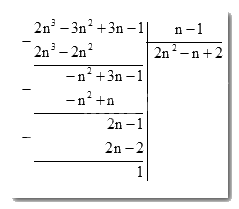
Vậy \(2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1\)
Để \(2{n^3} - 3{n^2} + 3n - 1\) chia hết cho \(n - 1\) thì \(1\) chia hết cho \(n - 1\).
\( \Rightarrow \left( {n - 1} \right) \in \left\{ {1; - 1} \right\}\)
Do đó n \( \in \) {0;2} để \(P \in Z\)
Vậy có 2 giá trị n thỏa mãn.
Tìm kết quả của phép chia 8x4 - 2x3 cho 4x2
2x2
4x5
2x2 - 0,5.x
2x2 + 1
Phép chia 2x4 – x3 + 2x – 1 cho x2 – x + 1 có thương là:
0,5. x2 + 2x – 1
- 2x2 + 2x – 1
2x2 + x – 1
2x2 + x + 1
Phép chia 2x5 – 3x3 + 1 cho -2x3 + 3 có dư là:
3x2 – 3,5
–x2 + 1,5
x2 - 1,5
-3x2 + 3,5
Thương của phép chia đa thức một biến bậc 6 cho đa thức một biến bậc 2 là đa thức bậc mấy?
2
3
4
Không xác định được
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
\({x^3} + 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} - 5x + 1\)
\({x^3} + 4{x^2} - 5x + 1\)
Tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 2\)
\(8\)
\(9\)
\(10\)
\(12\)
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
\(a = 0\) và \(b = - 16\)
\(a = 0\) và \(b = 16\)
\(a = 0\) và \(b = 0\)
\(a = 1\) và \(b = 1\)
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\):
\( - 4\)
\(2\)
\( - 2\)
\(4\)
Cho \(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Có bao nhiêu giá trị \(n \in Z\) để \(P \in Z\).
0
1
2
Vô số
Tìm kết quả của phép chia 8x4 - 2x3 cho 4x2
2x2
4x5
2x2 - 0,5.x
2x2 + 1
Đáp án : C
Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
Ta có:
(8x4 - 2x3) : 4x2 = 8x4 : 4x2 - 2x3 : 4x2 = 2x2 – 0,5.x
Phép chia 2x4 – x3 + 2x – 1 cho x2 – x + 1 có thương là:
0,5. x2 + 2x – 1
- 2x2 + 2x – 1
2x2 + x – 1
2x2 + x + 1
Đáp án : C
Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
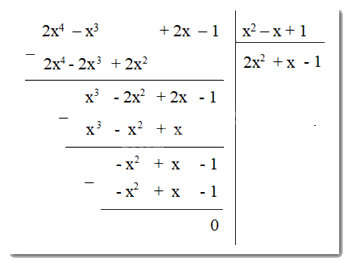
Phép chia 2x5 – 3x3 + 1 cho -2x3 + 3 có dư là:
3x2 – 3,5
–x2 + 1,5
x2 - 1,5
-3x2 + 3,5
Đáp án : A
Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
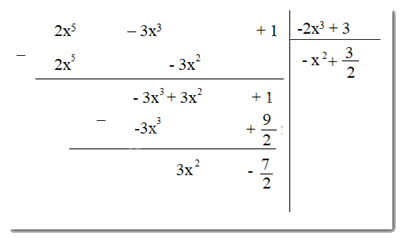
Vậy số dư là \(3x^2 - \frac{7}{2} = 3x^2 – 3,5\)
Thương của phép chia đa thức một biến bậc 6 cho đa thức một biến bậc 2 là đa thức bậc mấy?
2
3
4
Không xác định được
Đáp án : C
Viết dạng tổng quát của phép chia đa thức bậc 6 cho đa thức bậc 2
Ta có: Đa thức biến x bậc 6 có dạng: a6 . x6 + a5 . x5 + a4 . x4 + a3 . x3 + a2 . x2 + a1. x + a0 (a6 khác 0)
Đa thức biến x bậc 2 có dạng: b2 . x2 + b1. x + b0 (b2 khác 0)
Khi chia đa thức biến x bậc 6 cho đa thức biến x bậc 2, đầu tiên, ta lấy hạng tử : a6 . x6 chia cho b2 . x2 nên thu được đa thức thương có bậc là 6 – 2 = 4
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
\({x^3} + 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} + 5x + 1\)
\({x^3} - 4{x^2} - 5x + 1\)
\({x^3} + 4{x^2} - 5x + 1\)
Đáp án : A
Tìm đa thức A thỏa mãn A = B. Q + R
Trong đó, A là đa thức bị chia, B là đa thức chia, Q là thương, R là dư
Ta có: Đa thức bị chia = \(\left( {{x^2} + x + 1} \right)\). \(\left( {x + 3} \right)\) + \(x - 2\)
= x2 . (x + 3) + x. (x+3) + 1. (x+3) + x – 2
= x2 . x + x2 . 3 + x .x + x . 3 + 1. x + 1.3 + x – 2
= x3 + 3x2 + x2 + 3x + x + 3 + x – 2
= x3 + (3x2 + x2 ) + (3x + x + x ) + (3 – 2)
= x3 + 4x2 + 5x + 1
Tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 2\)
\(8\)
\(9\)
\(10\)
\(12\)
Đáp án : A
+) Chia đa thức cho đa thức: Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Thay x = 2 vào đa thức thương vừa thu được
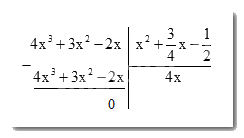
Tại \(x = 2\) , ta có: \(A = 4x = 4.2 = 8\)
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
\(a = 0\) và \(b = - 16\)
\(a = 0\) và \(b = 16\)
\(a = 0\) và \(b = 0\)
\(a = 1\) và \(b = 1\)
Đáp án : A
+) Chia đa thức cho đa thức: Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Biện luận để \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\) thì dư = 0, tìm a,b
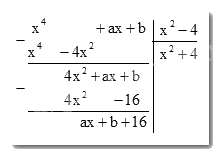
Để \({x^4} + ax + b\) chia hết cho \({x^2} - 4\) thì
\(ax + b + 16 = 0 \)
\(ax = 0\) và \(b + 16 = 0\)
suy ra \(a = 0\) và \(b = - 16\)
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\):
\( - 4\)
\(2\)
\( - 2\)
\(4\)
Đáp án : D
+) Chia đa thức cho đa thức: Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Biện luận để dư = 2
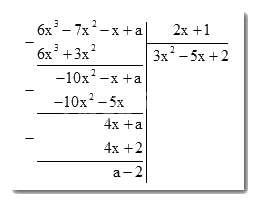
Để \(6{x^3} - 7{x^2} - x + a\) chia \(2x + 1\) dư \(2\) thì \(a - 2 = 2 \Leftrightarrow a = 4\).
Cho \(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Có bao nhiêu giá trị \(n \in Z\) để \(P \in Z\).
0
1
2
Vô số
Đáp án : C
- Đặt phép chia.
- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia nên số chia là ước của số dư cuối cùng.
- Lập bảng thử chọn để chọn ra giá trị của \(n\)thỏa mãn.
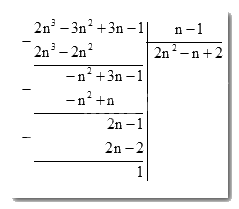
Vậy \(2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1\)
Để \(2{n^3} - 3{n^2} + 3n - 1\) chia hết cho \(n - 1\) thì \(1\) chia hết cho \(n - 1\).
\( \Rightarrow \left( {n - 1} \right) \in \left\{ {1; - 1} \right\}\)
Do đó n \( \in \) {0;2} để \(P \in Z\)
Vậy có 2 giá trị n thỏa mãn.
Bài 28 trong chương trình Toán 7 Kết nối tri thức tập trung vào việc giới thiệu và rèn luyện kỹ năng thực hiện phép chia đa thức một biến. Đây là một kỹ năng quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn ở các lớp trên. Bài học này bao gồm các nội dung chính sau:
Các bài tập trắc nghiệm về phép chia đa thức một biến thường xoay quanh các dạng sau:
Để giải dạng bài này, bạn cần hiểu rõ định nghĩa của các yếu tố trong phép chia đa thức một biến. Ví dụ:
Cho phép chia: (6x3 - 4x2 + 2x) : (2x)
Trong phép chia này:
Để thực hiện phép chia đa thức một biến, bạn có thể sử dụng phương pháp chia trực tiếp hoặc phương pháp đặt ẩn phụ. Ví dụ:
Chia (x2 + 5x + 6) cho (x + 2)
Sử dụng phương pháp chia trực tiếp:
| x | +3 | |
|---|---|---|
| x + 2 | x2 + 5x + 6 | |
| x2 + 2x | ||
| 3x + 6 | ||
| 3x + 6 | ||
| 0 |
Vậy thương là x + 3 và số dư là 0.
Trắc nghiệm Bài 28: Phép chia đa thức một biến Toán 7 Kết nối tri thức là một công cụ hữu ích để giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán. Hãy tận dụng tối đa bài trắc nghiệm này để đạt kết quả tốt nhất trong học tập.