Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh ôn luyện và kiểm tra kiến thức về hệ số góc của đường thẳng trong chương trình Toán 8 Kết nối tri thức. Các câu hỏi được thiết kế đa dạng, bao gồm nhiều mức độ khó khác nhau, giúp học sinh rèn luyện kỹ năng giải bài tập.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp tài liệu học tập chất lượng và phương pháp giải bài tập hiệu quả.
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Chọn khẳng định đúng nhất:
Đường thẳng \(y = \frac{{3x + 1}}{3}\) có hệ số góc là:
Chọn đáp án đúng.
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\)
Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d.
Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\)
Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Cho hàm số bậc nhất \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3\left( 1 \right)\)
Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Lời giải và đáp án
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Đáp án : B
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Đáp án : D
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\)
Vì đường thẳng \(y = ax + b\) có hệ số góc bằng 2 nên \(a = 2\left( {tm} \right)\)
Do đó hàm số: \(y = 2x + b\)
Đường thẳng \(y = 2x + b\) cắt trục tung tại điểm có tung độ bằng \( - 1\) nên \(y = - 1;x = 0\)
Ta có: \( - 1 = 2.0 + b\)
\(b = - 1\)
Do đó, hàm số cần tìm là: \(y = 2x - 1\)
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Đáp án : A
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Đáp án : C
Chọn khẳng định đúng nhất:
Đáp án : C
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại, trùng nhau khi \(a = a',b = b'\) và ngược lại
+ Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại, trùng nhau khi \(a = a',b = b'\) và ngược lại
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Đường thẳng \(y = \frac{{3x + 1}}{3}\) có hệ số góc là:
Chọn đáp án đúng.
Đáp án : B
Ta có: \(y = \frac{{3x + 1}}{3} = x + \frac{1}{3}\) nên hệ số góc của đường thẳng là 1
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Đáp án : D
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
Để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) thì \(2 \ne 1\) (luôn đúng) và \(m + 1 = - 2\)
\(m = - 3\) (thỏa mãn)
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Đáp án : C
Để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) thì \(m - 1 \ne 2\)
\(m \ne 3\) (thỏa mãn)
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Đáp án : C
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\) trùng nhau khi: \(1 = 1\) (luôn đúng) và \(2m = m + 1\)
\(m = 1\) (thỏa mãn)
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\)
Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Đáp án : D
Các cặp 2 đường thẳng cắt nhau là:
\(y = x + 5\) và \(y = - x + 5\); \(y = x + 5\) và \(y = - x + 3\); \(y = - x + 5\) và \(y = x + 7\); \(y = x + 7\) và \(y = - x + 3\)
Do đó, có 4 cặp hai đường thẳng cắt nhau.
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Đáp án : A
Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
Hàm số \(y = 2mx + 1\) là hàm số bậc nhất khi \(m \ne 0,\) hàm số \(y = \left( {m + 1} \right)x + m\) là hàm số bậc nhất khi \(m \ne - 1\)
Để hai đường thẳng \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\) song song với nhau thì
\(\left\{ \begin{array}{l}2m = m + 1\\m \ne 1\end{array} \right. \Rightarrow \)\(\left\{ \begin{array}{l}m = 1\\m \ne 1\end{array} \right.\), do đó không có giá trị nào của m thỏa mãn bài toán.
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Đáp án : C
Hàm số cần tìm có dạng \(y = 3x + b\left( {b \ne 1} \right)\)
Vì đường thẳng cần tìm đi qua điểm (1;7) nên ta có: \(7 = 3.1 + b,\) tìm được \(b = 4\) (thỏa mãn)
Vậy hàm số cần tìm là \(y = 3x + 4\)
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đáp án : C
Gọi phương trình đường thẳng d cần tìm là \(y = ax + b\left( {a \ne 0} \right)\)
Vì d đi qua gốc tọa độ nên \(b = 0 \Rightarrow y = ax\)
Vì điểm M(2; 6) thuộc d nên \(6 = 2a,\) \(a = 3\) (thỏa mãn)
Phương trình đường thẳng d: \(y = 3x\) nên hệ số góc của đường thẳng d là 3.
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Đáp án : B
Vì điểm A(1; 9) thuộc đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\) nên:
\(9 = 2\left( {m + 1} \right).1 + m - 2\)
\(3m = 9\)
\(m = 3\) (thỏa mãn)
Đường thẳng d: \(y = 8x + 1\), do đó đường thẳng d có hệ số góc là 8
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Đáp án : B
d là hàm số bậc nhất khi \(m \ne 2\)
\(d':y = - 2x - 2mx + 3 = \left( { - 2 - 2m} \right)x + 3\)
d’ là hàm số bậc nhất khi \(m \ne - 1\)
Hai đường thẳng thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = \left( { - 2 - 2m} \right)x + 3\) cắt nhau thì:
\(m - 2 \ne - 2 - 2m\)
\(3m \ne 0\)
\(m \ne 0\) (thỏa mãn)
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Đáp án : A
d là hàm số bậc nhất khi \(m \ne - 2\)
Hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\) trùng nhau khi:
\(\left\{ \begin{array}{l}m + 2 = - 2\\m = - 2m + 1\end{array} \right.\; \Leftrightarrow \;\left\{ \begin{array}{l}m = - 4\\m = \frac{1}{3}\end{array} \right.\) (vô lí)
Vậy không có giá trị nào của m thỏa mãn bài toán
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d.
Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\)
Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Đáp án : D
Hàm số \(y = 2ax + a - 1\) là hàm số bậc nhất khi \(a \ne 0\)
d’: \(y - 4x + 3 = 0\), \(y = 4x - 3\)
Vì đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y = 4x - 3\) nên hệ số góc của đường thẳng d bằng 8, hay \(2a = 8,\) \(a = 4\) (thỏa mãn)
Do đó, d: \(y = 8x + 3\)
Vì điểm A(x; 6) thuộc đường thẳng d nên \(6 = 8.x + 3\)
\(x = \frac{3}{8}\)
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Đáp án : C
\(\frac{x}{3} + \frac{y}{2} = 1\)
\(\frac{{2x}}{3} + y = 2\)
\(y = \frac{{ - 2x}}{3} + 2\)
Do đó, hệ số góc của đường thẳng trên là \(\frac{{ - 2}}{3}\)
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Đáp án : D
Đường thẳng có dạng \(y = mx + n\) (d)
Vì đường thẳng d đi qua điểm A(m; 3) nên \(3 = {m^2} + n\) (1)
Vì đường thẳng d đi qua điểm B(1; m) nên \(m = m + n\), tìm được \(n = 0\)
Thay \(n = 0\) vào (1) ta có: \({m^2} = 3,\) tìm được \(m = \pm \sqrt 3 \)
Mà \(m > 0\) nên \(m = \sqrt 3 \)
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Đáp án : C
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
+ Đồ thị hàm số bậc nhất
Hàm số \(y = mx + 3\) là hàm số bậc nhất khi \(m \ne 0\)
Vì đường thẳng d song song với đường thẳng \(y = - x\) nên \(m = - 1\) (thỏa mãn)
Do đó, d: \(y = - x + 3\)
Vẽ đồ thị của hai hàm số: \(y = - x + 3\) và \(y = x + 1\):
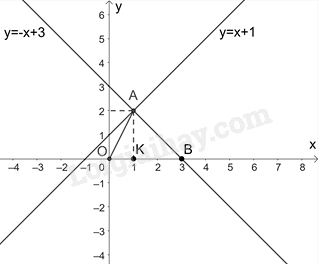
Nhìn vào đồ thị ta thấy, A(1; 2), B(3; 0), do đó, \(OB = 3\)
Gọi K là hình chiếu của A trên trục Ox, do đó AK là đường cao trong tam giác OAB và \(AK = 2\)
Diện tích tam giác OAB là: \(S = \frac{1}{2}AK.OB = \frac{1}{2}.3.2 = 3\) (đvdt)
Cho hàm số bậc nhất \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3\left( 1 \right)\)
Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Đáp án : B
Ta có: \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3 = \left( {\frac{1}{2}{m^2} - \frac{1}{4}m} \right)x + {m^{10}} - {m^4} + 3\)
Hàm số (1) là hàm số bậc nhất khi \(\frac{1}{2}{m^2} - \frac{1}{4}m \ne 0\), tìm được \(m \ne 0,m \ne \frac{1}{2}\)
Ta có: \(\frac{1}{2}{m^2} - \frac{1}{4}m = \frac{1}{2}\left( {{m^2} - \frac{1}{2}m} \right) = \frac{1}{2}\left( {{m^2} - 2.m.\frac{1}{4} + \frac{1}{{16}} - \frac{1}{{16}}} \right) = \frac{1}{2}{\left( {m - \frac{1}{4}} \right)^2} - \frac{1}{{32}} \ge \frac{{ - 1}}{{32}}\)
Do đó, hệ số góc của đồ thị hàm số (1) đạt giá trị nhỏ nhất là \(\frac{{ - 1}}{{32}}\) khi \(m - \frac{1}{4} = 0\), \(m = \frac{1}{4}\) (thỏa mãn)
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Chọn khẳng định đúng nhất:
Đường thẳng \(y = \frac{{3x + 1}}{3}\) có hệ số góc là:
Chọn đáp án đúng.
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\)
Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d.
Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\)
Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Cho hàm số bậc nhất \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3\left( 1 \right)\)
Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Đáp án : B
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Đáp án : D
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\)
Vì đường thẳng \(y = ax + b\) có hệ số góc bằng 2 nên \(a = 2\left( {tm} \right)\)
Do đó hàm số: \(y = 2x + b\)
Đường thẳng \(y = 2x + b\) cắt trục tung tại điểm có tung độ bằng \( - 1\) nên \(y = - 1;x = 0\)
Ta có: \( - 1 = 2.0 + b\)
\(b = - 1\)
Do đó, hàm số cần tìm là: \(y = 2x - 1\)
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Đáp án : A
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Đáp án : C
Chọn khẳng định đúng nhất:
Đáp án : C
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại, trùng nhau khi \(a = a',b = b'\) và ngược lại
+ Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại, trùng nhau khi \(a = a',b = b'\) và ngược lại
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Đường thẳng \(y = \frac{{3x + 1}}{3}\) có hệ số góc là:
Chọn đáp án đúng.
Đáp án : B
Ta có: \(y = \frac{{3x + 1}}{3} = x + \frac{1}{3}\) nên hệ số góc của đường thẳng là 1
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Đáp án : D
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
Để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) thì \(2 \ne 1\) (luôn đúng) và \(m + 1 = - 2\)
\(m = - 3\) (thỏa mãn)
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Đáp án : C
Để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) thì \(m - 1 \ne 2\)
\(m \ne 3\) (thỏa mãn)
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Đáp án : C
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\) trùng nhau khi: \(1 = 1\) (luôn đúng) và \(2m = m + 1\)
\(m = 1\) (thỏa mãn)
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\)
Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Đáp án : D
Các cặp 2 đường thẳng cắt nhau là:
\(y = x + 5\) và \(y = - x + 5\); \(y = x + 5\) và \(y = - x + 3\); \(y = - x + 5\) và \(y = x + 7\); \(y = x + 7\) và \(y = - x + 3\)
Do đó, có 4 cặp hai đường thẳng cắt nhau.
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Đáp án : A
Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
Hàm số \(y = 2mx + 1\) là hàm số bậc nhất khi \(m \ne 0,\) hàm số \(y = \left( {m + 1} \right)x + m\) là hàm số bậc nhất khi \(m \ne - 1\)
Để hai đường thẳng \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\) song song với nhau thì
\(\left\{ \begin{array}{l}2m = m + 1\\m \ne 1\end{array} \right. \Rightarrow \)\(\left\{ \begin{array}{l}m = 1\\m \ne 1\end{array} \right.\), do đó không có giá trị nào của m thỏa mãn bài toán.
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Đáp án : C
Hàm số cần tìm có dạng \(y = 3x + b\left( {b \ne 1} \right)\)
Vì đường thẳng cần tìm đi qua điểm (1;7) nên ta có: \(7 = 3.1 + b,\) tìm được \(b = 4\) (thỏa mãn)
Vậy hàm số cần tìm là \(y = 3x + 4\)
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đáp án : C
Gọi phương trình đường thẳng d cần tìm là \(y = ax + b\left( {a \ne 0} \right)\)
Vì d đi qua gốc tọa độ nên \(b = 0 \Rightarrow y = ax\)
Vì điểm M(2; 6) thuộc d nên \(6 = 2a,\) \(a = 3\) (thỏa mãn)
Phương trình đường thẳng d: \(y = 3x\) nên hệ số góc của đường thẳng d là 3.
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Đáp án : B
Vì điểm A(1; 9) thuộc đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\) nên:
\(9 = 2\left( {m + 1} \right).1 + m - 2\)
\(3m = 9\)
\(m = 3\) (thỏa mãn)
Đường thẳng d: \(y = 8x + 1\), do đó đường thẳng d có hệ số góc là 8
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Đáp án : B
d là hàm số bậc nhất khi \(m \ne 2\)
\(d':y = - 2x - 2mx + 3 = \left( { - 2 - 2m} \right)x + 3\)
d’ là hàm số bậc nhất khi \(m \ne - 1\)
Hai đường thẳng thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = \left( { - 2 - 2m} \right)x + 3\) cắt nhau thì:
\(m - 2 \ne - 2 - 2m\)
\(3m \ne 0\)
\(m \ne 0\) (thỏa mãn)
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Đáp án : A
d là hàm số bậc nhất khi \(m \ne - 2\)
Hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\) trùng nhau khi:
\(\left\{ \begin{array}{l}m + 2 = - 2\\m = - 2m + 1\end{array} \right.\; \Leftrightarrow \;\left\{ \begin{array}{l}m = - 4\\m = \frac{1}{3}\end{array} \right.\) (vô lí)
Vậy không có giá trị nào của m thỏa mãn bài toán
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d.
Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\)
Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Đáp án : D
Hàm số \(y = 2ax + a - 1\) là hàm số bậc nhất khi \(a \ne 0\)
d’: \(y - 4x + 3 = 0\), \(y = 4x - 3\)
Vì đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y = 4x - 3\) nên hệ số góc của đường thẳng d bằng 8, hay \(2a = 8,\) \(a = 4\) (thỏa mãn)
Do đó, d: \(y = 8x + 3\)
Vì điểm A(x; 6) thuộc đường thẳng d nên \(6 = 8.x + 3\)
\(x = \frac{3}{8}\)
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Đáp án : C
\(\frac{x}{3} + \frac{y}{2} = 1\)
\(\frac{{2x}}{3} + y = 2\)
\(y = \frac{{ - 2x}}{3} + 2\)
Do đó, hệ số góc của đường thẳng trên là \(\frac{{ - 2}}{3}\)
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Đáp án : D
Đường thẳng có dạng \(y = mx + n\) (d)
Vì đường thẳng d đi qua điểm A(m; 3) nên \(3 = {m^2} + n\) (1)
Vì đường thẳng d đi qua điểm B(1; m) nên \(m = m + n\), tìm được \(n = 0\)
Thay \(n = 0\) vào (1) ta có: \({m^2} = 3,\) tìm được \(m = \pm \sqrt 3 \)
Mà \(m > 0\) nên \(m = \sqrt 3 \)
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Đáp án : C
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
+ Đồ thị hàm số bậc nhất
Hàm số \(y = mx + 3\) là hàm số bậc nhất khi \(m \ne 0\)
Vì đường thẳng d song song với đường thẳng \(y = - x\) nên \(m = - 1\) (thỏa mãn)
Do đó, d: \(y = - x + 3\)
Vẽ đồ thị của hai hàm số: \(y = - x + 3\) và \(y = x + 1\):

Nhìn vào đồ thị ta thấy, A(1; 2), B(3; 0), do đó, \(OB = 3\)
Gọi K là hình chiếu của A trên trục Ox, do đó AK là đường cao trong tam giác OAB và \(AK = 2\)
Diện tích tam giác OAB là: \(S = \frac{1}{2}AK.OB = \frac{1}{2}.3.2 = 3\) (đvdt)
Cho hàm số bậc nhất \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3\left( 1 \right)\)
Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Đáp án : B
Ta có: \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3 = \left( {\frac{1}{2}{m^2} - \frac{1}{4}m} \right)x + {m^{10}} - {m^4} + 3\)
Hàm số (1) là hàm số bậc nhất khi \(\frac{1}{2}{m^2} - \frac{1}{4}m \ne 0\), tìm được \(m \ne 0,m \ne \frac{1}{2}\)
Ta có: \(\frac{1}{2}{m^2} - \frac{1}{4}m = \frac{1}{2}\left( {{m^2} - \frac{1}{2}m} \right) = \frac{1}{2}\left( {{m^2} - 2.m.\frac{1}{4} + \frac{1}{{16}} - \frac{1}{{16}}} \right) = \frac{1}{2}{\left( {m - \frac{1}{4}} \right)^2} - \frac{1}{{32}} \ge \frac{{ - 1}}{{32}}\)
Do đó, hệ số góc của đồ thị hàm số (1) đạt giá trị nhỏ nhất là \(\frac{{ - 1}}{{32}}\) khi \(m - \frac{1}{4} = 0\), \(m = \frac{1}{4}\) (thỏa mãn)
Bài 29 trong chương trình Toán 8 Kết nối tri thức tập trung vào việc tìm hiểu về hệ số góc của đường thẳng. Hệ số góc là một khái niệm quan trọng trong hình học, giúp xác định độ dốc của đường thẳng. Hiểu rõ về hệ số góc sẽ giúp học sinh giải quyết các bài toán liên quan đến đường thẳng một cách dễ dàng và chính xác.
Hệ số góc của đường thẳng được ký hiệu là k. Nó thể hiện độ dốc của đường thẳng so với trục hoành. Nếu đường thẳng đi lên từ trái sang phải thì hệ số góc dương, nếu đường thẳng đi xuống từ trái sang phải thì hệ số góc âm. Đường thẳng song song với trục hoành có hệ số góc bằng 0.
Có nhiều cách để xác định hệ số góc của đường thẳng:
Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc. Hai đường thẳng vuông góc khi và chỉ khi tích của hệ số góc của chúng bằng -1 (k1 * k2 = -1).
Các bài tập trắc nghiệm về hệ số góc thường tập trung vào các dạng sau:
Ví dụ 1: Xác định hệ số góc của đường thẳng có phương trình y = 3x - 2.
Giải: Hệ số góc của đường thẳng là k = 3.
Ví dụ 2: Xác định hệ số góc của đường thẳng đi qua hai điểm A(1, 2) và B(3, 6).
Giải: Hệ số góc của đường thẳng là k = (6 - 2) / (3 - 1) = 4 / 2 = 2.
Để nắm vững kiến thức về hệ số góc, các em học sinh nên luyện tập thường xuyên các bài tập trắc nghiệm. Dưới đây là một số câu hỏi trắc nghiệm để các em tham khảo:
Hệ số góc là một khái niệm cơ bản và quan trọng trong hình học. Việc nắm vững kiến thức về hệ số góc sẽ giúp học sinh giải quyết các bài toán liên quan đến đường thẳng một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải bài tập.