Chào mừng các em học sinh đến với bài trắc nghiệm Bài 33: Hai tam giác đồng dạng môn Toán 8 chương trình Kết nối tri thức. Bài trắc nghiệm này được thiết kế để giúp các em ôn luyện và củng cố kiến thức về các trường hợp đồng dạng của tam giác, định lý Thales và ứng dụng của chúng.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, bao gồm các câu hỏi từ dễ đến khó, có đáp án chi tiết để các em tự đánh giá năng lực của mình.
Hãy chọn câu đúng.
Hãy chọn câu sai.
Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng
Hãy chọn câu đúng
Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số
Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:
Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng
Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?
Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:
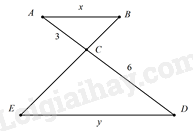
Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng
Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:
Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)
\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)
\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)
Chọn câu đúng:
Cho tam giác ABC, lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
12cm.
36cm.
Lời giải và đáp án
Hãy chọn câu đúng.
Đáp án : A
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên câu A đúng, câu C sai.
+ Hai tam giác đồng dạng thì chưa chắc bằng nhau nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1 nên câu B sai.
+ Hai tam giác vuông chưa chắc đồng dạng (chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau) nên câu D sai.
Hãy chọn câu sai.
Đáp án : C
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên A đúng.
+ Hai tam giác đều có các góc đều bằng \({60^0}\) và các cạnh của mỗi tam giác bằng nhau nên các cạnh tương ứng tỉ lệ . Vậy hai tam giác đều luôn đồng dạng nên B đúng.
+ Hai tam giác cân chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau nên không đồng dạng nên C sai
+ Câu D đúng vì là định nghĩa hai tam giác đồng dạng.
Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
Đáp án : A
\(\Delta ABC \backsim \Delta MNP \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}}\\{\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P}\end{array}} \right.\)
Mà \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P(gt)\)
nên cần bổ sung thêm điều kiện \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) thì \(\Delta ABC \backsim \Delta MNP\) (định nghĩa).
Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng
Đáp án : D
Vì \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2 (gt) \( \Rightarrow BC = 2NP\)
Hãy chọn câu đúng
Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số
Đáp án : B
Vì \(\Delta ABC \backsim \Delta MNP\) theo tỉ số đồng dạng là \(k = \frac{2}{3}\) \( \Rightarrow \Delta MNP \backsim \Delta ABC\) theo tỉ số đồng dạng là \(\frac{1}{k} = \frac{3}{2}\)
Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:
Đáp án : C
\(\Delta ABC\) có \(\widehat C = {180^o} - \left( {\widehat A + \widehat B} \right) = {180^o} - \left( {{{90}^o} + {{80}^o}} \right) = {30^o}\) (Định lý tổng ba góc trong tam giác )
\(\Delta MNP\) có \(\widehat N = {180^o} - \left( {\widehat M + \widehat P} \right) = {180^o} - \left( {{{90}^o} + {{30}^o}} \right) = {60^o}\) (Định lý tổng ba góc trong tam giác)
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\frac{{AB}}{{MN}} = \frac{{18}}{6} = 3;\frac{{AC}}{{MP}} = \frac{{24}}{8} = 3;\frac{{BC}}{{NP}} = \frac{{30}}{{10}} = 3\)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\)
Vậy \(\widehat A = \widehat M\left( { = {{90}^o}} \right);\widehat B = \widehat N\left( { = {{60}^o}} \right);\widehat C = \widehat P\left( { = {{30}^o}} \right)\)
Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng
Đáp án : A
Vì \(\Delta ABC \backsim \Delta D{\rm{EF}} \Rightarrow \widehat A = \widehat D\) (hai góc tương ứng)
Mà \(\widehat A = {50^o}(gt) \Rightarrow \widehat D = {50^o}\)
Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
Đáp án : A
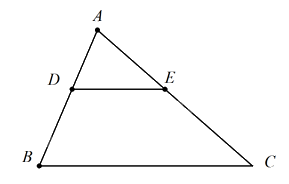
Vì \(DE//BC \left( {gt} \right)\Rightarrow \Delta ABC \backsim \Delta A{\rm{D}}E\)
Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?
Đáp án : C
Vì \(\Delta ABC \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_1} \Rightarrow \frac{{AB}}{{DE}} = {k_1}\)
Vì \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2} \Rightarrow \frac{{MN}}{{DE}} = {k_2}\)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{AB}}{{DE}}:\frac{{MN}}{{DE}} = \frac{{{k_1}}}{{{k_2}}}\)
Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:
Đáp án : B
Vì \(\Delta ABC \backsim \Delta MNP \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (hai cạnh tương ứng)
\(\begin{array}{l} \Rightarrow \frac{5}{{10}} = \frac{{AC}}{5} = \frac{6}{{NP}}\\ \Rightarrow AC = \frac{{5.5}}{{10}} = 2,5cm;NP = \frac{{10.6}}{5} = 12cm\end{array}\)
Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.
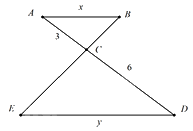
Đáp án : D
Vì AB // DE \( \Rightarrow \Delta ABC \backsim \Delta DEC\) (định lí)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{C{\rm{D}}}}\) (các cạnh tương ứng) \( \Rightarrow \frac{x}{y} = \frac{3}{6} = \frac{1}{2}\)
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng
Đáp án : B
Vì \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3 \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{2}{3}\)
Vì \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số \(1:3 \Rightarrow \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{1}{3}\)
\( \Rightarrow \frac{{AB}}{{{A_2}{B_2}}} = \frac{{AB}}{{{A_1}{B_1}}}.\frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{2}{3}.\frac{1}{3} = \frac{2}{9}\)
Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số \(k = 2:9\) .
Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:
Đáp án : D
Vì \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) .
\(\begin{array}{l} \Rightarrow \frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{B_1} + {A_1}{C_1} + {B_1}{C_1}}}{{AB + AC + BC}} = \frac{2}{3}\\ \Rightarrow \frac{{C{V_{\Delta {A_1}{B_1}{C_1}}}}}{{C{V_{\Delta ABC}}}} = \frac{2}{3}\end{array}\)
Hai tam giác đồng dạng theo tỉ số nào thì chu vi cũng đồng dạng theo tỉ số đó.
Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
Đáp án : D
Vì\(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\)
\(\begin{array}{l} \Rightarrow \frac{{MN}}{{AB}} = \frac{{MI}}{{AC}} = \frac{{NI}}{{BC}} = \frac{{MN + MI + NI}}{{AB + AC + BC}} = \frac{5}{7}\\ \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{C{V_{\Delta ABC}}}} = \frac{5}{7} \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{C{V_{\Delta ABC}} - C{V_{\Delta MNI}}}} = \frac{5}{{7 - 5}}\\ \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{16}} = \frac{5}{2} \Rightarrow C{V_{\Delta MNI}} = \frac{{16.5}}{2} = 40(cm).\\ \Rightarrow C{V_{\Delta ABC}} = 40 + 16 = 56(cm).\end{array}\)
Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)
\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)
\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)
Chọn câu đúng:
Đáp án : C
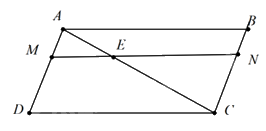
Xét \(\Delta A{\rm{D}}C\) có \(ME//C{\rm{D}}\) (gt) \( \Rightarrow \Delta AM{\rm{E}} \backsim \Delta A{\rm{D}}C(1)\) theo tỉ số đồng dạng \({k_1} = \frac{{A{\rm{E}}}}{{AC}} = \frac{1}{3}\)
Vì ABCD là hình bình hành nên
+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} \)
+ \(AB//C{\rm{D}} \Rightarrow \widehat {BAC} = \widehat {AC{\rm{D}}}\) (so le trong)
+ \(AD//BC \Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\) (so le trong)
+ AD = BC ; AB = CD
Xét \(\Delta CBA\) và \(\Delta A{\rm{D}}C\) có :
+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} ;\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {ACB} = \widehat {CA{\rm{D}}}(cmt)\)
+ \(\frac{{AB}}{{C{\rm{D}}}} = \frac{{BC}}{{A{\rm{D}}}} = \frac{{AC}}{{AC}}( = 1)\)
\( \Rightarrow \Delta CBA \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_2} = 1\)
Xét \(\Delta ABC\) có :
EN//CD (gt) mà AB//CD (cmt)
\( \Rightarrow EN//AB \Rightarrow \Delta CNE \backsim \Delta CBA\)
Mà \(\Delta CBA \backsim \Delta A{\rm{D}}C(cmt)\)
\( \Rightarrow \Delta CNE \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_3} = \frac{{CE}}{{AC}} = \frac{2}{3}\) (Vì \(AC = 3{\rm{AE}} \Rightarrow CE = \frac{2}{3}AC)\)
Vậy khẳng định (I), (II), (III) đều đúng.
Cho tam giác ABC, lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
12cm.
36cm.
Đáp án : A
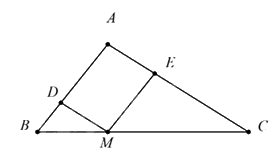
Vì MD // AC nên \( \Delta DBM \backsim \Delta ABC\)
Vì ME // AB nên \(\Delta EMC \backsim \Delta ABC\)
Suy ra \(\Delta DBM \backsim \Delta EMC\left( { \backsim \Delta ABC} \right)\)
Do đó:
\(\frac{{DB}}{{EM}} = \frac{{DM}}{{EC}} = \frac{{BM}}{{MC}} = \frac{{DB + DM + BM}}{{EM + EC + MC}} = \frac{1}{2}\)
nên \(\frac{{C{V_{\Delta DBM}}}}{{C{V_{\Delta EMC}}}} = \frac{1}{2}\)
Mà chu vi tam giác MEC bằng 24 cm
Chu vi tam giác DBM bằng 24 : 2 = 12 (cm).
Hãy chọn câu đúng.
Hãy chọn câu sai.
Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng
Hãy chọn câu đúng
Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số
Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:
Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng
Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?
Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:
Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.

Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng
Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:
Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)
\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)
\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)
Chọn câu đúng:
Cho tam giác ABC, lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
12cm.
36cm.
Hãy chọn câu đúng.
Đáp án : A
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên câu A đúng, câu C sai.
+ Hai tam giác đồng dạng thì chưa chắc bằng nhau nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1 nên câu B sai.
+ Hai tam giác vuông chưa chắc đồng dạng (chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau) nên câu D sai.
Hãy chọn câu sai.
Đáp án : C
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên A đúng.
+ Hai tam giác đều có các góc đều bằng \({60^0}\) và các cạnh của mỗi tam giác bằng nhau nên các cạnh tương ứng tỉ lệ . Vậy hai tam giác đều luôn đồng dạng nên B đúng.
+ Hai tam giác cân chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau nên không đồng dạng nên C sai
+ Câu D đúng vì là định nghĩa hai tam giác đồng dạng.
Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
Đáp án : A
\(\Delta ABC \backsim \Delta MNP \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}}\\{\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P}\end{array}} \right.\)
Mà \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P(gt)\)
nên cần bổ sung thêm điều kiện \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) thì \(\Delta ABC \backsim \Delta MNP\) (định nghĩa).
Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng
Đáp án : D
Vì \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2 (gt) \( \Rightarrow BC = 2NP\)
Hãy chọn câu đúng
Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số
Đáp án : B
Vì \(\Delta ABC \backsim \Delta MNP\) theo tỉ số đồng dạng là \(k = \frac{2}{3}\) \( \Rightarrow \Delta MNP \backsim \Delta ABC\) theo tỉ số đồng dạng là \(\frac{1}{k} = \frac{3}{2}\)
Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:
Đáp án : C
\(\Delta ABC\) có \(\widehat C = {180^o} - \left( {\widehat A + \widehat B} \right) = {180^o} - \left( {{{90}^o} + {{80}^o}} \right) = {30^o}\) (Định lý tổng ba góc trong tam giác )
\(\Delta MNP\) có \(\widehat N = {180^o} - \left( {\widehat M + \widehat P} \right) = {180^o} - \left( {{{90}^o} + {{30}^o}} \right) = {60^o}\) (Định lý tổng ba góc trong tam giác)
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\frac{{AB}}{{MN}} = \frac{{18}}{6} = 3;\frac{{AC}}{{MP}} = \frac{{24}}{8} = 3;\frac{{BC}}{{NP}} = \frac{{30}}{{10}} = 3\)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\)
Vậy \(\widehat A = \widehat M\left( { = {{90}^o}} \right);\widehat B = \widehat N\left( { = {{60}^o}} \right);\widehat C = \widehat P\left( { = {{30}^o}} \right)\)
Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng
Đáp án : A
Vì \(\Delta ABC \backsim \Delta D{\rm{EF}} \Rightarrow \widehat A = \widehat D\) (hai góc tương ứng)
Mà \(\widehat A = {50^o}(gt) \Rightarrow \widehat D = {50^o}\)
Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
Đáp án : A

Vì \(DE//BC \left( {gt} \right)\Rightarrow \Delta ABC \backsim \Delta A{\rm{D}}E\)
Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?
Đáp án : C
Vì \(\Delta ABC \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_1} \Rightarrow \frac{{AB}}{{DE}} = {k_1}\)
Vì \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2} \Rightarrow \frac{{MN}}{{DE}} = {k_2}\)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{AB}}{{DE}}:\frac{{MN}}{{DE}} = \frac{{{k_1}}}{{{k_2}}}\)
Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:
Đáp án : B
Vì \(\Delta ABC \backsim \Delta MNP \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (hai cạnh tương ứng)
\(\begin{array}{l} \Rightarrow \frac{5}{{10}} = \frac{{AC}}{5} = \frac{6}{{NP}}\\ \Rightarrow AC = \frac{{5.5}}{{10}} = 2,5cm;NP = \frac{{10.6}}{5} = 12cm\end{array}\)
Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.

Đáp án : D
Vì AB // DE \( \Rightarrow \Delta ABC \backsim \Delta DEC\) (định lí)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{C{\rm{D}}}}\) (các cạnh tương ứng) \( \Rightarrow \frac{x}{y} = \frac{3}{6} = \frac{1}{2}\)
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng
Đáp án : B
Vì \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3 \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{2}{3}\)
Vì \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số \(1:3 \Rightarrow \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{1}{3}\)
\( \Rightarrow \frac{{AB}}{{{A_2}{B_2}}} = \frac{{AB}}{{{A_1}{B_1}}}.\frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{2}{3}.\frac{1}{3} = \frac{2}{9}\)
Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số \(k = 2:9\) .
Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:
Đáp án : D
Vì \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) .
\(\begin{array}{l} \Rightarrow \frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{B_1} + {A_1}{C_1} + {B_1}{C_1}}}{{AB + AC + BC}} = \frac{2}{3}\\ \Rightarrow \frac{{C{V_{\Delta {A_1}{B_1}{C_1}}}}}{{C{V_{\Delta ABC}}}} = \frac{2}{3}\end{array}\)
Hai tam giác đồng dạng theo tỉ số nào thì chu vi cũng đồng dạng theo tỉ số đó.
Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
Đáp án : D
Vì\(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\)
\(\begin{array}{l} \Rightarrow \frac{{MN}}{{AB}} = \frac{{MI}}{{AC}} = \frac{{NI}}{{BC}} = \frac{{MN + MI + NI}}{{AB + AC + BC}} = \frac{5}{7}\\ \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{C{V_{\Delta ABC}}}} = \frac{5}{7} \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{C{V_{\Delta ABC}} - C{V_{\Delta MNI}}}} = \frac{5}{{7 - 5}}\\ \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{16}} = \frac{5}{2} \Rightarrow C{V_{\Delta MNI}} = \frac{{16.5}}{2} = 40(cm).\\ \Rightarrow C{V_{\Delta ABC}} = 40 + 16 = 56(cm).\end{array}\)
Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)
\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)
\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)
Chọn câu đúng:
Đáp án : C

Xét \(\Delta A{\rm{D}}C\) có \(ME//C{\rm{D}}\) (gt) \( \Rightarrow \Delta AM{\rm{E}} \backsim \Delta A{\rm{D}}C(1)\) theo tỉ số đồng dạng \({k_1} = \frac{{A{\rm{E}}}}{{AC}} = \frac{1}{3}\)
Vì ABCD là hình bình hành nên
+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} \)
+ \(AB//C{\rm{D}} \Rightarrow \widehat {BAC} = \widehat {AC{\rm{D}}}\) (so le trong)
+ \(AD//BC \Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\) (so le trong)
+ AD = BC ; AB = CD
Xét \(\Delta CBA\) và \(\Delta A{\rm{D}}C\) có :
+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} ;\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {ACB} = \widehat {CA{\rm{D}}}(cmt)\)
+ \(\frac{{AB}}{{C{\rm{D}}}} = \frac{{BC}}{{A{\rm{D}}}} = \frac{{AC}}{{AC}}( = 1)\)
\( \Rightarrow \Delta CBA \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_2} = 1\)
Xét \(\Delta ABC\) có :
EN//CD (gt) mà AB//CD (cmt)
\( \Rightarrow EN//AB \Rightarrow \Delta CNE \backsim \Delta CBA\)
Mà \(\Delta CBA \backsim \Delta A{\rm{D}}C(cmt)\)
\( \Rightarrow \Delta CNE \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_3} = \frac{{CE}}{{AC}} = \frac{2}{3}\) (Vì \(AC = 3{\rm{AE}} \Rightarrow CE = \frac{2}{3}AC)\)
Vậy khẳng định (I), (II), (III) đều đúng.
Cho tam giác ABC, lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
12cm.
36cm.
Đáp án : A

Vì MD // AC nên \( \Delta DBM \backsim \Delta ABC\)
Vì ME // AB nên \(\Delta EMC \backsim \Delta ABC\)
Suy ra \(\Delta DBM \backsim \Delta EMC\left( { \backsim \Delta ABC} \right)\)
Do đó:
\(\frac{{DB}}{{EM}} = \frac{{DM}}{{EC}} = \frac{{BM}}{{MC}} = \frac{{DB + DM + BM}}{{EM + EC + MC}} = \frac{1}{2}\)
nên \(\frac{{C{V_{\Delta DBM}}}}{{C{V_{\Delta EMC}}}} = \frac{1}{2}\)
Mà chu vi tam giác MEC bằng 24 cm
Chu vi tam giác DBM bằng 24 : 2 = 12 (cm).
Bài 33 trong chương trình Toán 8 Kết nối tri thức tập trung vào việc nghiên cứu về hai tam giác đồng dạng. Đây là một trong những kiến thức nền tảng quan trọng trong hình học, giúp học sinh hiểu rõ hơn về mối quan hệ giữa các tam giác và ứng dụng trong giải quyết các bài toán thực tế.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ. Ký hiệu: △ABC ~ △A'B'C'. Điều kiện cần và đủ để hai tam giác đồng dạng là:
Có ba trường hợp đồng dạng của tam giác thường được sử dụng:
Định lý Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác đồng dạng với tam giác đã cho.
Ứng dụng: Định lý Thales được sử dụng để tính tỉ số giữa các đoạn thẳng trên các cạnh của tam giác, giải các bài toán liên quan đến sự đồng dạng của tam giác.
Dưới đây là một số bài tập trắc nghiệm minh họa để giúp các em hiểu rõ hơn về kiến thức đã học:
Câu 1: Cho △ABC và △A'B'C' có ∠A = ∠A', ∠B = ∠B'. Kết luận nào sau đây là đúng?
Câu 2: Cho △ABC có AB = 3cm, BC = 4cm, CA = 5cm. △A'B'C' đồng dạng với △ABC và có tỉ số đồng dạng là 2. Độ dài các cạnh của △A'B'C' là:
Để nắm vững kiến thức về hai tam giác đồng dạng, các em nên:
Bài 33: Hai tam giác đồng dạng là một kiến thức quan trọng trong chương trình Toán 8. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Chúc các em học tốt!
| Trường hợp đồng dạng | Điều kiện |
|---|---|
| c-g-c | Hai cạnh tương ứng tỉ lệ và góc xen giữa bằng nhau |
| g-c-g | Hai góc tương ứng bằng nhau |
| c-c-c | Ba cạnh tương ứng tỉ lệ |
| Bảng tóm tắt các trường hợp đồng dạng của tam giác | |