Bài học về độ dài đoạn thẳng và đường gấp khúc là một trong những kiến thức cơ bản và quan trọng nhất trong chương trình Hình học lớp 6.
Hiểu rõ khái niệm này giúp học sinh làm quen với các phép đo độ dài, tính toán và ứng dụng vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp bài giảng chi tiết, bài tập đa dạng và phương pháp giải dễ hiểu để giúp bạn nắm vững kiến thức này.
Giải Độ dài đoạn thẳng. Độ dài đường gấp khúc trang 88, 89 SGK Toán 2 Cánh diều
Bài 2 (trang 87 SGK Toán 2 tập 1)
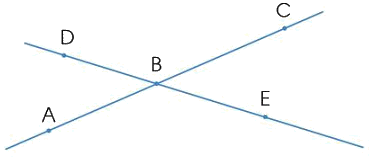
Nêu tên ba điểm thẳng hàng:
Phương pháp giải:
Quan sát kĩ hình vẽ đã cho, nếu ba điểm cùng nằm trên một đường thẳng thì ba điểm đó thẳng hàng.
Lời giải chi tiết:
Ba điểm thẳng hàng là có trong hình là:
- B, D, E là ba điểm thẳng hàng.
- A, B, C là ba điểm thẳng hàng.
Bài 1 (trang 86 SGK Toán 2 tập 1)
Chỉ ra đường thẳng, đường cong trong mỗi hình sau:
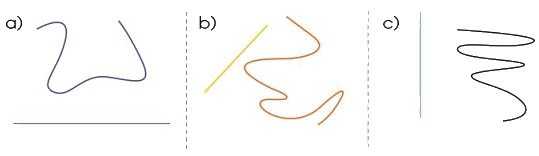
Phương pháp giải:
Quan sát kĩ các hình đã cho rồi chỉ ra đường thẳng, đường cong trong mỗi hình.
Lời giải chi tiết:
a) Đường màu đỏ là đường thẳng, đường màu xanh là đường cong.
b) Đường màu vàng là đường thẳng, đường màu cam là đường cong.
c) Đường màu xanh là đường thẳng, đường màu đen là đường cong.
Bài 3 (trang 87 SGK Toán 2 tập 1)
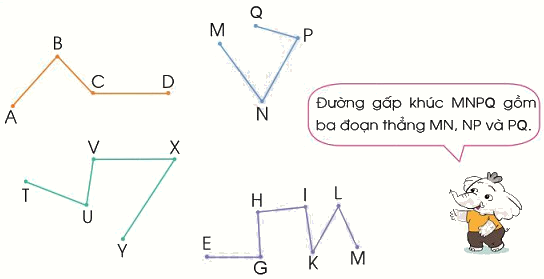
Nêu tên các đoạn thẳng của mỗi đường gấp khúc dưới đây:
Phương pháp giải:
Quan sát kĩ hình vẽ đã cho rồi nêu tên các đoạn thẳng của mỗi đường gấp khúc.
Lời giải chi tiết:
Đường gấp khúc ABCD gồm ba đoạn thẳng AB, BC và CD.
Đường gấp khúc MNPQ gồm ba đoạn thẳng MN, NP và PQ.
Đường gấp khúc TUVXY gồm bốn đoạn thẳng TU, UV, VX và XY.
Đường gấp khúc EGHIKLM gồm sáu đoạn thẳng EG, GH, HI, IK, KL và LM.
Bài 1 (trang 86 SGK Toán 2 tập 1)
Chỉ ra đường thẳng, đường cong trong mỗi hình sau:
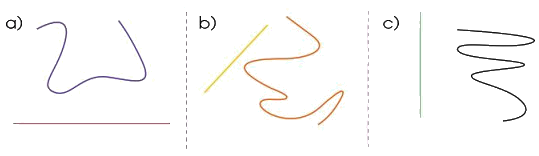
Phương pháp giải:
Quan sát kĩ các hình đã cho rồi chỉ ra đường thẳng, đường cong trong mỗi hình.
Lời giải chi tiết:
a) Đường màu đỏ là đường thẳng, đường màu xanh là đường cong.
b) Đường màu vàng là đường thẳng, đường màu cam là đường cong.
c) Đường màu xanh là đường thẳng, đường màu đen là đường cong.
Bài 2 (trang 87 SGK Toán 2 tập 1)
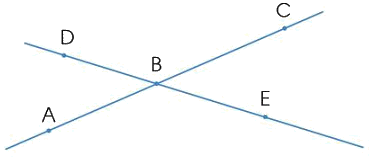
Nêu tên ba điểm thẳng hàng:
Phương pháp giải:
Quan sát kĩ hình vẽ đã cho, nếu ba điểm cùng nằm trên một đường thẳng thì ba điểm đó thẳng hàng.
Lời giải chi tiết:
Ba điểm thẳng hàng là có trong hình là:
- B, D, E là ba điểm thẳng hàng.
- A, B, C là ba điểm thẳng hàng.
Bài 3 (trang 87 SGK Toán 2 tập 1)
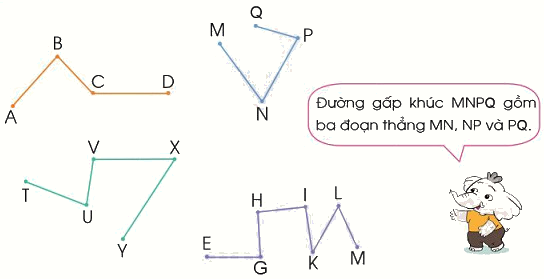
Nêu tên các đoạn thẳng của mỗi đường gấp khúc dưới đây:
Phương pháp giải:
Quan sát kĩ hình vẽ đã cho rồi nêu tên các đoạn thẳng của mỗi đường gấp khúc.
Lời giải chi tiết:
Đường gấp khúc ABCD gồm ba đoạn thẳng AB, BC và CD.
Đường gấp khúc MNPQ gồm ba đoạn thẳng MN, NP và PQ.
Đường gấp khúc TUVXY gồm bốn đoạn thẳng TU, UV, VX và XY.
Đường gấp khúc EGHIKLM gồm sáu đoạn thẳng EG, GH, HI, IK, KL và LM.
Bài 4 (trang SGK Toán 2 tập 1)
Tìm hai hình ảnh tạo bởi đường cong, đường gấp khúc trong bức tranh sau:

Phương pháp giải:
Quan sát kĩ bức tranh đã cho rồi tìm hai hình ảnh tạo bởi đường cong, đường gấp khúc trong bức tranh
Lời giải chi tiết:
Hai hình ảnh tạo bởi đường cong trong bức tranh là hình ảnh hai đám mây.
Hai hình ảnh tạo bởi đường gấp khúc trong bức tranh là hình ảnh đám cỏ màu xanh và hình ảnh các ngọn núi liền nhau.
Bài 4 (trang SGK Toán 2 tập 1)
Tìm hai hình ảnh tạo bởi đường cong, đường gấp khúc trong bức tranh sau:

Phương pháp giải:
Quan sát kĩ bức tranh đã cho rồi tìm hai hình ảnh tạo bởi đường cong, đường gấp khúc trong bức tranh
Lời giải chi tiết:
Hai hình ảnh tạo bởi đường cong trong bức tranh là hình ảnh hai đám mây.
Hai hình ảnh tạo bởi đường gấp khúc trong bức tranh là hình ảnh đám cỏ màu xanh và hình ảnh các ngọn núi liền nhau.
Trong hình học, đoạn thẳng là một phần của đường thẳng giới hạn bởi hai điểm. Độ dài đoạn thẳng là khoảng cách giữa hai điểm đó. Việc hiểu rõ khái niệm này là nền tảng cho việc học các khái niệm hình học phức tạp hơn.
Một đoạn thẳng AB được xác định bởi hai điểm A và B. Điểm A và B được gọi là điểm cuối của đoạn thẳng. Độ dài đoạn thẳng AB được ký hiệu là AB.
Độ dài đoạn thẳng có thể được đo bằng thước kẻ, compa hoặc các đơn vị đo độ dài khác như cm, m, km, inch, feet,...
Đường gấp khúc là một đường gồm các đoạn thẳng liên tiếp nối với nhau. Độ dài đường gấp khúc là tổng độ dài của tất cả các đoạn thẳng tạo nên đường gấp khúc đó.
Để tính độ dài đường gấp khúc, ta cộng độ dài của tất cả các đoạn thẳng thành phần.
Ví dụ: Cho đường gấp khúc ABCDE gồm các đoạn thẳng AB = 2cm, BC = 3cm, CD = 1cm, DE = 4cm. Độ dài đường gấp khúc ABCDE là: 2 + 3 + 1 + 4 = 10cm.
Bài 1: Đo độ dài đoạn thẳng MN trên hình vẽ (giả sử có hình vẽ). Hướng dẫn: Sử dụng thước kẻ để đo trực tiếp.
Bài 2: Một người đi bộ từ A đến B rồi đến C theo đường gấp khúc ABC. Biết AB = 50m, BC = 30m. Hỏi người đó đã đi được bao nhiêu mét?
Hướng dẫn: Độ dài đường gấp khúc ABC là: 50 + 30 = 80m.
Kiến thức về độ dài đoạn thẳng và đường gấp khúc được ứng dụng rộng rãi trong thực tế:
Ngoài ra, bạn có thể tìm hiểu thêm về:
Để củng cố kiến thức, bạn nên luyện tập thêm các bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú và đa dạng về độ dài đoạn thẳng và đường gấp khúc, giúp bạn tự tin hơn trong quá trình học tập.
Độ dài đoạn thẳng và đường gấp khúc là những khái niệm cơ bản nhưng vô cùng quan trọng trong hình học. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn.