Hình học và Đo lường là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán học, từ cấp Tiểu học đến Trung học Phổ thông. Việc nắm vững kiến thức về hai lĩnh vực này không chỉ giúp học sinh giải quyết các bài toán cụ thể mà còn phát triển tư duy logic, khả năng không gian và ứng dụng thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống ôn tập toàn diện về Hình học và Đo lường, được thiết kế để giúp bạn củng cố kiến thức, rèn luyện kỹ năng và tự tin đối mặt với mọi thử thách.
Giải Ôn tập về hình học và đo lường trang 98, 99 SGK Toán 2 Cánh diều
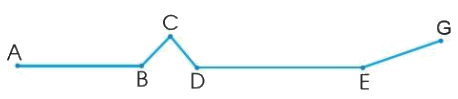
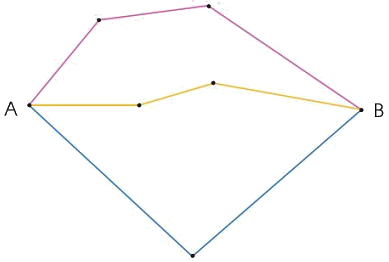
Đo và tính độ dài đường gấp khúc ABCDEG sau:
Phương pháp giải:
Độ dài đường gấp khúc ABCDEG = tổng độ dài các đoạn thẳng AB, BC, CD, DE, EG.
Lời giải chi tiết:
Độ dài đường gấp khúc ABCDEG là 3 + 1 + 1 + 4 + 2 = 11 (cm)
Nam nhảy dây từ mấy giờ đến mấy giờ?
Phương pháp giải:
Xem đồng hồ trong hình vẽ rồi trả lời câu hỏi.
Lời giải chi tiết:
Nam nhảy dây từ 8 giờ 15 phút đến 8 giờ 30 phút.
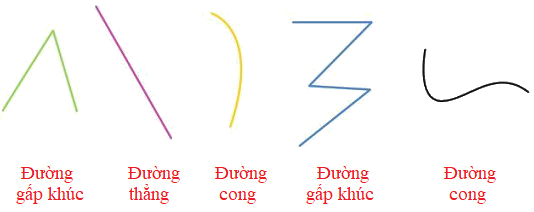
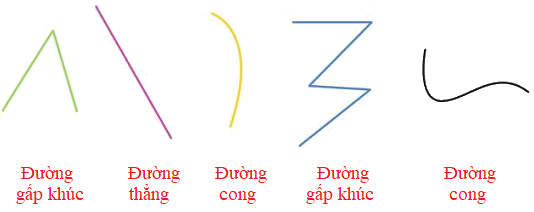
a) Chỉ ra đường thẳng, đường cong, đường gấp khúc trong hình sau:

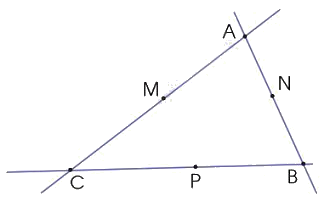
b) Đọc tên các điểm và các đoạn thẳng trong hình sau:
c) Vẽ đoạn thẳng MN có độ dài 6 cm.
Phương pháp giải:
Quan sát hình vẽ đẻ chỉ ra các đường thẳng, đường cong, đường gấp khúc, các điểm và các đoạn thẳng trong hình.
Lời giải chi tiết:
a)
b) Các điểm trong hình là: A, B, C, D, E, G.
Các đoạn thẳng có trong hình là: AB, BC, AD, DC, DE, CG, EG.
c) Đoạn thẳng MNcó độ dài 6 cm:
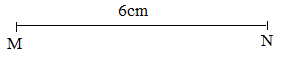
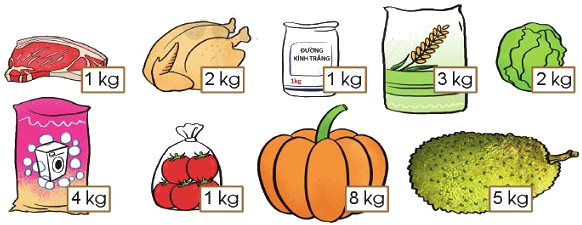
Một thang máy chở được tối đa 600 kg. Hiện tại, thang máy đó đã chở 570 kg. Bạn Lan cân nặng 35 kg. Theo em bạn Lan có thể vào tiếp trong thang máy đó được không?
Phương pháp giải:
- Tính số cân nặng mà thang máy còn chở được = Số cân nặng tối đa – Số cân nặng hiện tại trong thang máy.
- So sánh với cân nặng của Lan rồi trả lời câu hỏi.
Lời giải chi tiết:
Số cân nặng mà thang máy còn chở được là
600 – 570 = 30 (kg)
Vậy Lan không thể vào tiếp trong thang máy đó.
Ước lượng chiều cao cột cờ trường em.

Phương pháp giải:
Quan sát cột cờ của trường em và ước lượng chiều cao của cột cờ.
Lời giải chi tiết:
Ví dụ: Cột cờ trường em cao khoảng 10 m.
Số?
Phương pháp giải:
Quan sát hình vẽ em đếm số hình tam giác, hình tứ giác, hình trụ, khối cầu rồi trả lời câu hỏi.
Lời giải chi tiết:
a) Chỉ ra đường thẳng, đường cong, đường gấp khúc trong hình sau:

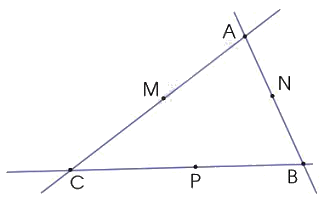
b) Đọc tên các điểm và các đoạn thẳng trong hình sau:
c) Vẽ đoạn thẳng MN có độ dài 6 cm.
Phương pháp giải:
Quan sát hình vẽ đẻ chỉ ra các đường thẳng, đường cong, đường gấp khúc, các điểm và các đoạn thẳng trong hình.
Lời giải chi tiết:
a)
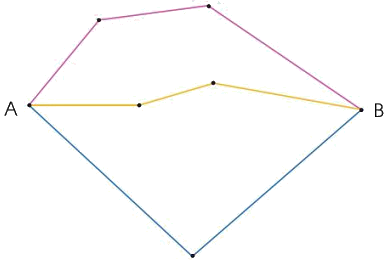
b) Các điểm trong hình là: A, B, C, D, E, G.
Các đoạn thẳng có trong hình là: AB, BC, AD, DC, DE, CG, EG.
c) Đoạn thẳng MNcó độ dài 6 cm:
Số?
Phương pháp giải:
Quan sát hình vẽ em đếm số hình tam giác, hình tứ giác, hình trụ, khối cầu rồi trả lời câu hỏi.
Lời giải chi tiết:

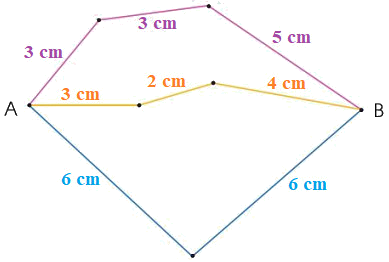
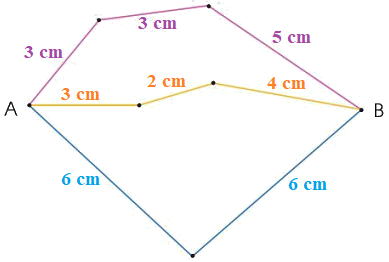
Đo và tính độ dài đường gấp khúc ABCDEG sau:
Phương pháp giải:
Độ dài đường gấp khúc ABCDEG = tổng độ dài các đoạn thẳng AB, BC, CD, DE, EG.
Lời giải chi tiết:
Độ dài đường gấp khúc ABCDEG là 3 + 1 + 1 + 4 + 2 = 11 (cm)
Nam nhảy dây từ mấy giờ đến mấy giờ?
Phương pháp giải:
Xem đồng hồ trong hình vẽ rồi trả lời câu hỏi.
Lời giải chi tiết:
Nam nhảy dây từ 8 giờ 15 phút đến 8 giờ 30 phút.
Một thang máy chở được tối đa 600 kg. Hiện tại, thang máy đó đã chở 570 kg. Bạn Lan cân nặng 35 kg. Theo em bạn Lan có thể vào tiếp trong thang máy đó được không?
Phương pháp giải:
- Tính số cân nặng mà thang máy còn chở được = Số cân nặng tối đa – Số cân nặng hiện tại trong thang máy.
- So sánh với cân nặng của Lan rồi trả lời câu hỏi.
Lời giải chi tiết:
Số cân nặng mà thang máy còn chở được là
600 – 570 = 30 (kg)
Vậy Lan không thể vào tiếp trong thang máy đó.
Ước lượng chiều cao cột cờ trường em.
Phương pháp giải:
Quan sát cột cờ của trường em và ước lượng chiều cao của cột cờ.
Lời giải chi tiết:
Ví dụ: Cột cờ trường em cao khoảng 10 m.
Hình học và Đo lường là hai nhánh quan trọng của Toán học, liên quan mật thiết đến việc nghiên cứu về hình dạng, kích thước và các mối quan hệ không gian. Việc nắm vững kiến thức về hai lĩnh vực này là nền tảng cho nhiều môn học khác, cũng như ứng dụng trong đời sống hàng ngày.
Hình học tập trung vào nghiên cứu các hình dạng, kích thước, vị trí tương đối của các đối tượng trong không gian. Các khái niệm cơ bản trong hình học bao gồm:
Phương pháp giải bài tập hình học:
Đo lường là quá trình xác định kích thước, khối lượng, thời gian và các đại lượng khác bằng các đơn vị đo lường. Các khái niệm cơ bản trong đo lường bao gồm:
Công thức đo lường quan trọng:
| Hình | Công thức tính diện tích | Công thức tính chu vi |
|---|---|---|
| Hình vuông | S = a² | P = 4a |
| Hình chữ nhật | S = a * b | P = 2(a + b) |
| Hình tròn | S = πr² | C = 2πr |
Hình học và Đo lường có mối liên hệ mật thiết với nhau. Hình học cung cấp các hình dạng và kích thước, trong khi Đo lường giúp chúng ta xác định và tính toán các đại lượng liên quan đến hình dạng và kích thước đó. Ví dụ, để tính diện tích của một hình chữ nhật, chúng ta cần biết chiều dài và chiều rộng (các đại lượng đo lường) và áp dụng công thức diện tích (liên quan đến hình học).
Kiến thức về Hình học và Đo lường được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, bao gồm:
Kết luận: Ôn tập về Hình học và Đo lường là một quá trình quan trọng để xây dựng nền tảng Toán học vững chắc. Bằng cách nắm vững các khái niệm cơ bản, phương pháp giải bài tập và ứng dụng thực tế, bạn sẽ tự tin hơn trong việc giải quyết các vấn đề Toán học và ứng dụng kiến thức vào cuộc sống.