Bài viết này cung cấp một bản tổng hợp toàn diện về các yếu tố cơ bản của thống kê và xác suất, dành cho học sinh, sinh viên và những ai muốn củng cố kiến thức toán học của mình.
Chúng ta sẽ cùng nhau ôn lại các khái niệm quan trọng, công thức tính toán và phương pháp giải bài tập thường gặp trong lĩnh vực này.
Giaitoan.edu.vn hy vọng sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán liên quan đến thống kê và xác suất.
Xem tranh rồi kiểm đếm số lượng từng loại con vật và ghi lại kết quả (theo mẫu). Quan sát biểu đồ tranh sau. Trả lời các câu hỏi sau: a) Biểu đồ tranh trên cho ta biết điều gì? b) Bạn Khôi uống mấy cốc nước trong một ngày? c) Bạn nào uống nhiều nước nhất? Bạn nào uống ít nước nhất? Hà và Nam chơi trò “Bịt mắt chọn hoa”.Chọn chữ đặt trước câu mô tả đúng khả năng xảy ra của một lần chơi:
Quan sát biểu đồ tranh sau:
Số cốc nước uống trong một ngày
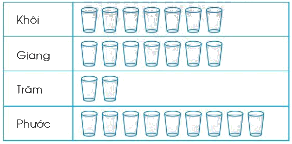
Trả lời các câu hỏi sau:
a) Biểu đồ tranh trên cho ta biết điều gì?
b) Bạn Khôi uống mấy cốc nước trong một ngày?
c) Bạn nào uống nhiều nước nhất? Bạn nào uống ít nước nhất?
Phương pháp giải:
Quan sát biểu đồ tranh, đếm số cốc nước mỗi bạn uống được rồi trả lời câu hỏi.
Lời giải chi tiết:
a) Biểu đồ trên cho biết số cốc nước uống trong một ngày của các bạn Khôi, Giang, Trâm, Phước.
b) Bạn Khôi uống 7 cốc nước trong một ngày.
c) Bạn Phước uống nhiều nước nhất. Bạn Trâm uống ít nước nhất.
Hà và Nam chơi trò “Bịt mắt chọn hoa”.
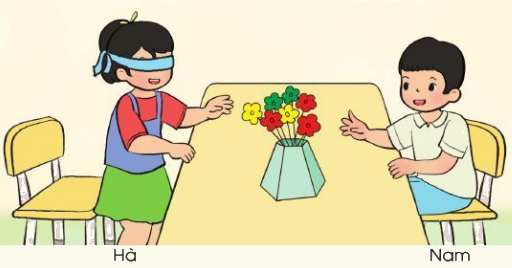
Chọn chữ đặt trước câu mô tả đúng khả năng xảy ra của một lần chơi:
A. Hà có thể chọn được bông hoa màu vàng.
B. Hà có thể chọn được bông hoa màu vàng.
C. Hà có thể chọn được bông hoa màu vàng.
Phương pháp giải:
Quan sát tranh ta thấy Lọ hoa gồm các bông hoa màu vàng, đỏ, xanh từ đó em chọn được câu thích hợp.
Lời giải chi tiết:
Quan sát tranh ta thấy Lọ hoa gồm các bông hoa màu vàng, đỏ, xanh.
Vậy Hà có thể chọn được bông hoa màu vàng.
Chọn A.
Có 5 thẻ ghi các số 1, 2, 3, 4, 5. Hãy rút ra một thẻ và đọc số ghi trên thẻ đó.

Sử dụng các từ “chắc chắn”, “có thể”, “không thể” để mô tả đúng khả năng xảy ra của một lần rút thẻ.
a) Thẻ được rút ra là thẻ ghi số 0.
b) Thẻ được rút ra là thẻ ghi số 1.
c) Thẻ được rút ra là thẻ ghi một số bé hơn 10.
Phương pháp giải:
Quan sát tranh rồi sử dụng các từ “chắc chắn”, “có thể”, “không thể” với mỗi tình huống được đưa ra.
Lời giải chi tiết:
a) Thẻ được rút ra không thể là thẻ ghi số 0.
b) Thẻ được rút ra có thể là thẻ ghi số 1.
c) Thẻ được rút ra chắc chắn là thẻ ghi một số bé hơn 10.
Xem tranh rồi kiểm đếm số lượng từng loại con vật và ghi lại kết quả (theo mẫu):

Phương pháp giải:
Xem tranh rồi đếm số lượng mỗi con vật và ghi lại kết quả theo ví dụ mẫu.
Lời giải chi tiết:

Xem tranh rồi kiểm đếm số lượng từng loại con vật và ghi lại kết quả (theo mẫu):

Phương pháp giải:
Xem tranh rồi đếm số lượng mỗi con vật và ghi lại kết quả theo ví dụ mẫu.
Lời giải chi tiết:

Quan sát biểu đồ tranh sau:
Số cốc nước uống trong một ngày
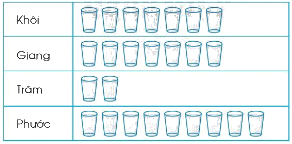
Trả lời các câu hỏi sau:
a) Biểu đồ tranh trên cho ta biết điều gì?
b) Bạn Khôi uống mấy cốc nước trong một ngày?
c) Bạn nào uống nhiều nước nhất? Bạn nào uống ít nước nhất?
Phương pháp giải:
Quan sát biểu đồ tranh, đếm số cốc nước mỗi bạn uống được rồi trả lời câu hỏi.
Lời giải chi tiết:
a) Biểu đồ trên cho biết số cốc nước uống trong một ngày của các bạn Khôi, Giang, Trâm, Phước.
b) Bạn Khôi uống 7 cốc nước trong một ngày.
c) Bạn Phước uống nhiều nước nhất. Bạn Trâm uống ít nước nhất.
Hà và Nam chơi trò “Bịt mắt chọn hoa”.
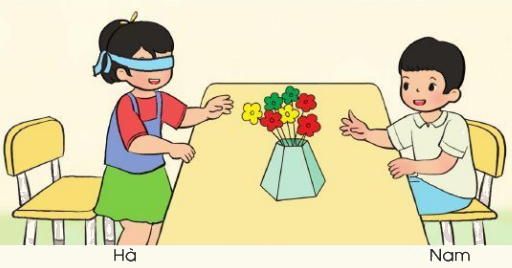
Chọn chữ đặt trước câu mô tả đúng khả năng xảy ra của một lần chơi:
A. Hà có thể chọn được bông hoa màu vàng.
B. Hà có thể chọn được bông hoa màu vàng.
C. Hà có thể chọn được bông hoa màu vàng.
Phương pháp giải:
Quan sát tranh ta thấy Lọ hoa gồm các bông hoa màu vàng, đỏ, xanh từ đó em chọn được câu thích hợp.
Lời giải chi tiết:
Quan sát tranh ta thấy Lọ hoa gồm các bông hoa màu vàng, đỏ, xanh.
Vậy Hà có thể chọn được bông hoa màu vàng.
Chọn A.
Có 5 thẻ ghi các số 1, 2, 3, 4, 5. Hãy rút ra một thẻ và đọc số ghi trên thẻ đó.

Sử dụng các từ “chắc chắn”, “có thể”, “không thể” để mô tả đúng khả năng xảy ra của một lần rút thẻ.
a) Thẻ được rút ra là thẻ ghi số 0.
b) Thẻ được rút ra là thẻ ghi số 1.
c) Thẻ được rút ra là thẻ ghi một số bé hơn 10.
Phương pháp giải:
Quan sát tranh rồi sử dụng các từ “chắc chắn”, “có thể”, “không thể” với mỗi tình huống được đưa ra.
Lời giải chi tiết:
a) Thẻ được rút ra không thể là thẻ ghi số 0.
b) Thẻ được rút ra có thể là thẻ ghi số 1.
c) Thẻ được rút ra chắc chắn là thẻ ghi một số bé hơn 10.
Thống kê và xác suất là hai lĩnh vực toán học quan trọng, có ứng dụng rộng rãi trong nhiều ngành khoa học, kỹ thuật và đời sống. Việc nắm vững kiến thức về thống kê và xác suất giúp chúng ta hiểu rõ hơn về thế giới xung quanh, đưa ra những quyết định sáng suốt dựa trên dữ liệu và dự đoán các sự kiện trong tương lai.
1. Dân số và mẫu: Dân số là tập hợp tất cả các đối tượng quan tâm trong một nghiên cứu. Mẫu là một tập hợp con của dân số, được chọn để đại diện cho dân số đó. Ví dụ, nếu chúng ta muốn nghiên cứu chiều cao trung bình của học sinh trong một trường, thì toàn bộ học sinh trong trường là dân số, và một nhóm học sinh được chọn ngẫu nhiên từ trường là mẫu.
2. Biến ngẫu nhiên: Biến ngẫu nhiên là một biến có giá trị phụ thuộc vào kết quả của một thí nghiệm ngẫu nhiên. Ví dụ, khi tung một đồng xu, biến ngẫu nhiên có thể là 'Mặt ngửa' hoặc 'Mặt sấp'.
3. Phân phối xác suất: Phân phối xác suất mô tả khả năng xảy ra của mỗi giá trị của một biến ngẫu nhiên. Ví dụ, phân phối xác suất của việc tung một đồng xu công bằng là 50% cho 'Mặt ngửa' và 50% cho 'Mặt sấp'.
4. Các loại biến:
1. Định nghĩa xác suất: Xác suất của một sự kiện là một số thực nằm trong khoảng từ 0 đến 1, biểu thị mức độ khả năng xảy ra của sự kiện đó. Xác suất bằng 0 có nghĩa là sự kiện không thể xảy ra, xác suất bằng 1 có nghĩa là sự kiện chắc chắn xảy ra.
2. Các quy tắc tính xác suất:
3. Xác suất có điều kiện: Xác suất có điều kiện của sự kiện A khi biết sự kiện B đã xảy ra là P(A|B) = P(A và B) / P(B).
1. Số trung bình (Mean): Là tổng của tất cả các giá trị chia cho số lượng giá trị. Công thức: μ = Σxi / n
2. Trung vị (Median): Là giá trị nằm ở giữa khi các giá trị được sắp xếp theo thứ tự tăng dần hoặc giảm dần.
3. Mốt (Mode): Là giá trị xuất hiện nhiều nhất trong một tập dữ liệu.
4. Độ lệch chuẩn (Standard Deviation): Đo lường mức độ phân tán của các giá trị xung quanh số trung bình. Công thức: σ = √[Σ(xi - μ)2 / n]
5. Phương sai (Variance): Là bình phương của độ lệch chuẩn. Công thức: σ2 = [Σ(xi - μ)2 / n]
1. Phân phối chuẩn (Normal Distribution): Là một phân phối xác suất liên tục, có dạng hình chuông. Nó được sử dụng rộng rãi trong thống kê để mô tả nhiều hiện tượng tự nhiên và xã hội.
2. Phân phối nhị thức (Binomial Distribution): Mô tả số lần thành công trong một số lượng cố định các thử nghiệm độc lập, mỗi thử nghiệm chỉ có hai kết quả có thể xảy ra (thành công hoặc thất bại).
3. Phân phối Poisson (Poisson Distribution): Mô tả số lượng sự kiện xảy ra trong một khoảng thời gian hoặc không gian nhất định.
Thống kê và xác suất có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Việc hiểu rõ các khái niệm và công thức trong thống kê và xác suất là rất quan trọng để có thể phân tích dữ liệu một cách chính xác và đưa ra những quyết định đúng đắn. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan về lĩnh vực này và giúp bạn tự tin hơn trong việc giải quyết các bài toán liên quan.