Bài học này tiếp tục rèn luyện kỹ năng phép cộng có nhớ trong phạm vi 100 cho học sinh. Chúng tôi cung cấp các bài tập đa dạng, từ cơ bản đến nâng cao, giúp các em tự tin giải quyết các bài toán cộng phức tạp.
Giaitoan.edu.vn cam kết mang đến phương pháp học toán online hiệu quả, giúp các em nắm vững kiến thức nền tảng và phát triển tư duy logic.
Giải Phép cộng (có nhớ) trong phạm vi 100 (tiếp theo) trang 60, 61 SGK Toán 2 Cánh diều
Nhi bật xa được 87 cm, Khôi bật xa hơn Nhi 5 cm. Hỏi Khôi bật xa được bao nhiêu xăng-ti-mét?
Phương pháp giải:
- Đọc kĩ đề bài để xác định đề bài cho biết gì (số xăng-ti-mét Nhi bật xa được, số xăng-ti-mét Khôi bật xa hơn Nhi) và hỏi gì (số xăng-ti-mét Khôi bật xa được), từ đó hoàn thành tóm tắt bài toán.
- Để tìm số xăng-ti-mét Khôi bật xa được ta lấy số xăng-ti-mét Nhi bật xa được cộng với số xăng-ti-mét Khôi bật xa hơn Nhi.
Lời giải chi tiết:
Tóm tắt
Nhi: 87 cm
Khôi bật xa hơn Nhi: 5 cm
Khôi:  cm
cm
Bài giải
Khôi bật xa được số xăng-ti-mét là:
87 + 5 = 92 (cm)
Đáp số: 92 cm.
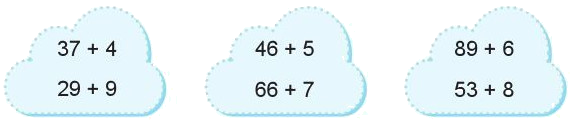
Đặt tính rồi tính:
Phương pháp giải:
- Đặt tính : Viết các chữ số cùng hàng thẳng cột với nhau.
- Tính : Cộng các chữ số lần lượt từ phải sang trái.
Lời giải chi tiết:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{37}\\{\,\,4}\end{array}}\\\hline{\,\,\,41}\end{array}\) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{29}\\{\,\,9}\end{array}}\\\hline{\,\,\,38}\end{array}\)
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{46}\\{\,\,5}\end{array}}\\\hline{\,\,\,51}\end{array}\) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{66}\\{\,\,7}\end{array}}\\\hline{\,\,\,73}\end{array}\)
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{89}\\{\,\,6}\end{array}}\\\hline{\,\,\,95}\end{array}\) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{53}\\{\,\,8}\end{array}}\\\hline{\,\,\,61}\end{array}\)
Tính:
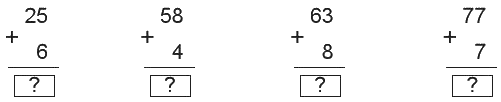
Phương pháp giải:
Thực hiện cộng lần lượt từ phải sang trái.
Lời giải chi tiết:
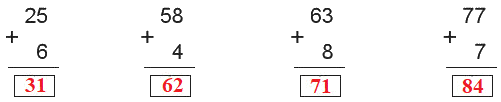
Tìm chữ số bị chú ong che khuất trong mỗi phép tính sau:

Lời giải chi tiết:
+) Phép tính 36 + 7.
Đặt tính rồi tính ta được:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{36}\\{\,\,\,7}\end{array}}\\\hline{\,\,\,\,43}\end{array}\)
Vậy chữ số bị chú ong che khuất là 4.
+) Phép tính thứ hai:
Ta thấy chữ số hàng chục ở tổng và số hạng thứ nhất đều là 7, do đó phép tính đã cho là phép tính không có nhớ.
Ở hàng đơn vị, ta có 6 + 2 = 8.
Phép tính đầy đủ như sau:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{76}\\{\,\,\,2}\end{array}}\\\hline{\,\,\,\,78}\end{array}\)
Vậy chữ số bị chú ong che khuất là 6.
+) Phép tính thứ ba:
Ở hàng đơn vị ta có: 6 + 5 = 11, do đó ta viết 1 ở hàng đơn vị, nhớ 1 sang hàng chục.
Quan sát ta thấy chữ số hàng chục ở tổng là 2, từ đó suy ra chữ số hàng chục ở số hạng thứ nhất là 1.
Phép tính đầy đủ như sau:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{16}\\{\,\,5}\end{array}}\\\hline{\,\,\,\,21}\end{array}\)
Vậy chữ số bị chú ong che khuất là 1.
Tính:
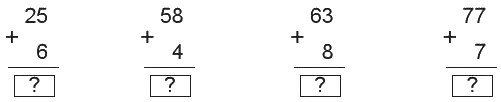
Phương pháp giải:
Thực hiện cộng lần lượt từ phải sang trái.
Lời giải chi tiết:
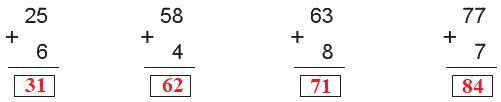
Đặt tính rồi tính:
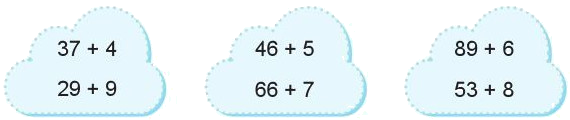
Phương pháp giải:
- Đặt tính : Viết các chữ số cùng hàng thẳng cột với nhau.
- Tính : Cộng các chữ số lần lượt từ phải sang trái.
Lời giải chi tiết:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{37}\\{\,\,4}\end{array}}\\\hline{\,\,\,41}\end{array}\) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{29}\\{\,\,9}\end{array}}\\\hline{\,\,\,38}\end{array}\)
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{46}\\{\,\,5}\end{array}}\\\hline{\,\,\,51}\end{array}\) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{66}\\{\,\,7}\end{array}}\\\hline{\,\,\,73}\end{array}\)
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{89}\\{\,\,6}\end{array}}\\\hline{\,\,\,95}\end{array}\) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{53}\\{\,\,8}\end{array}}\\\hline{\,\,\,61}\end{array}\)
Tìm chữ số bị chú ong che khuất trong mỗi phép tính sau:

Lời giải chi tiết:
+) Phép tính 36 + 7.
Đặt tính rồi tính ta được:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{36}\\{\,\,\,7}\end{array}}\\\hline{\,\,\,\,43}\end{array}\)
Vậy chữ số bị chú ong che khuất là 4.
+) Phép tính thứ hai:
Ta thấy chữ số hàng chục ở tổng và số hạng thứ nhất đều là 7, do đó phép tính đã cho là phép tính không có nhớ.
Ở hàng đơn vị, ta có 6 + 2 = 8.
Phép tính đầy đủ như sau:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{76}\\{\,\,\,2}\end{array}}\\\hline{\,\,\,\,78}\end{array}\)
Vậy chữ số bị chú ong che khuất là 6.
+) Phép tính thứ ba:
Ở hàng đơn vị ta có: 6 + 5 = 11, do đó ta viết 1 ở hàng đơn vị, nhớ 1 sang hàng chục.
Quan sát ta thấy chữ số hàng chục ở tổng là 2, từ đó suy ra chữ số hàng chục ở số hạng thứ nhất là 1.
Phép tính đầy đủ như sau:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{16}\\{\,\,5}\end{array}}\\\hline{\,\,\,\,21}\end{array}\)
Vậy chữ số bị chú ong che khuất là 1.
Nhi bật xa được 87 cm, Khôi bật xa hơn Nhi 5 cm. Hỏi Khôi bật xa được bao nhiêu xăng-ti-mét?
Phương pháp giải:
- Đọc kĩ đề bài để xác định đề bài cho biết gì (số xăng-ti-mét Nhi bật xa được, số xăng-ti-mét Khôi bật xa hơn Nhi) và hỏi gì (số xăng-ti-mét Khôi bật xa được), từ đó hoàn thành tóm tắt bài toán.
- Để tìm số xăng-ti-mét Khôi bật xa được ta lấy số xăng-ti-mét Nhi bật xa được cộng với số xăng-ti-mét Khôi bật xa hơn Nhi.
Lời giải chi tiết:
Tóm tắt
Nhi: 87 cm
Khôi bật xa hơn Nhi: 5 cm
Khôi:  cm
cm
Bài giải
Khôi bật xa được số xăng-ti-mét là:
87 + 5 = 92 (cm)
Đáp số: 92 cm.
Phép cộng có nhớ trong phạm vi 100 là một kỹ năng toán học cơ bản nhưng vô cùng quan trọng đối với học sinh tiểu học, đặc biệt là lớp 2 và lớp 3. Việc nắm vững kỹ năng này không chỉ giúp các em giải quyết các bài toán cộng đơn giản mà còn là nền tảng để học các phép tính phức tạp hơn như phép trừ, phép nhân, phép chia.
Trước khi đi vào luyện tập, chúng ta cần hiểu rõ khái niệm phép cộng có nhớ. Khi thực hiện phép cộng hai số mà tổng của chúng lớn hơn 9, chúng ta cần “nhớ” hàng đơn vị của tổng đó để cộng vào hàng chục. Ví dụ, trong phép cộng 7 + 5, tổng là 12. Chúng ta viết 2 ở hàng đơn vị và “nhớ” 1 lên hàng chục.
Hãy cùng xem xét ví dụ sau: 38 + 25
Có rất nhiều dạng bài tập khác nhau để luyện tập phép cộng có nhớ trong phạm vi 100. Dưới đây là một số dạng bài tập phổ biến:
Để học tập hiệu quả, các em có thể áp dụng một số mẹo sau:
Dưới đây là một số bài tập để các em luyện tập:
| Bài tập | Kết quả |
|---|---|
| 25 + 37 | |
| 48 + 16 | |
| 62 + 29 | |
| 71 + 19 |
Phép cộng có nhớ không chỉ là một kỹ năng toán học mà còn có ứng dụng rộng rãi trong cuộc sống hàng ngày. Ví dụ, khi chúng ta đi mua sắm, chúng ta cần cộng giá của các món hàng để biết tổng số tiền phải trả. Khi chúng ta tính toán số lượng đồ vật, chúng ta cũng cần sử dụng phép cộng.
Phép cộng (có nhớ) trong phạm vi 100 là một kỹ năng toán học quan trọng cần được rèn luyện thường xuyên. Hy vọng rằng, với những kiến thức và bài tập được cung cấp trong bài viết này, các em sẽ tự tin hơn trong việc giải quyết các bài toán cộng và đạt kết quả tốt trong học tập.