Bài học này sẽ giúp bạn hiểu rõ cách biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ. Chúng ta sẽ khám phá mối liên hệ giữa phương trình đại số và hình học, từ đó nắm vững kiến thức Toán 9 một cách trực quan và hiệu quả.
Giaitoan.edu.vn cung cấp bài giảng chi tiết, bài tập đa dạng và phương pháp giải dễ hiểu, giúp bạn tự tin chinh phục môn Toán.
Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của phương trình \(ax + by = c\).
Phương trình bậc nhất hai ẩn \(ax + by = c\) luôn luôn có vô số nghiệm.
Để xác định cặp số \(\left( {{x_0};{y_0}} \right)\) có là nghiệm của phương trình \(ax + by = c\) không, ta thay \(x = {x_0}\) và \(y = {y_0}\) vào phương trình \(ax + by = c\):
+ Nếu \(a{x_0} + b{y_0} = c\) thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình \(ax + by = c\).
+ Nếu \(a{x_0} + b{y_0} = c\) thì \(\left( {{x_0};{y_0}} \right)\) không là nghiệm của phương trình \(ax + by = c\).
- Trong mặt phẳng toạ độ Oxy, mỗi nghiệm của phương trình \(ax + by = c\) được biểu diễn bởi một điểm. Nghiệm \(\left( {{x_0};{y_0}} \right)\) được biểu diễn bởi điểm có toạ độ \(\left( {{x_0};{y_0}} \right)\).
- Tất cả các nghiệm của phương trình đó được biểu diễn bởi một đường thẳng.
+ Phương trình \(ax + 0y = c\left( {a \ne 0} \right)\)
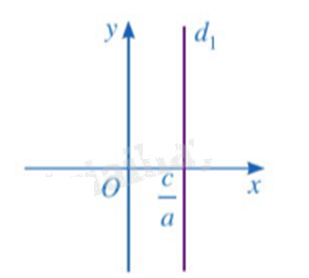
Mỗi nghiệm của phương trình \(ax + 0y = c\left( {a \ne 0} \right)\) được biểu diễn bởi điểm có toạ độ \(\left( {\frac{c}{a};{y_0}} \right)\) \(\left( {{y_0} \in \mathbb{R}} \right)\) nằm trên đường thẳng \({d_1}:x = \frac{c}{a}\). Đường thẳng \({d_1}\) là đường thẳng đi qua điểm \(\frac{c}{a}\) trên trục Ox và vuông góc với trục Ox.
+ Phương trình \(0x + by = c\left( {b \ne 0} \right)\)
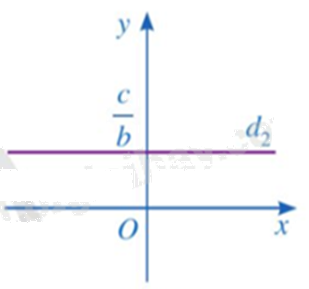
Mỗi nghiệm của phương trình \(0x + by = c\left( {b \ne 0} \right)\) được biểu diễn bởi một điểm có toạ độ \(\left( {{x_0};\frac{c}{b}} \right)\left( {{x_0} \in \mathbb{R}} \right)\) nằm trên đường thẳng \({d_2}:y = \frac{c}{b}\). Đường thẳng \({d_2}\) là đường thẳng đi qua điểm \(\frac{c}{b}\) trên trục Oy và vuông góc với trục Oy.
+ Phương trình \(ax + by = c\left( {a \ne 0,b \ne 0} \right)\)
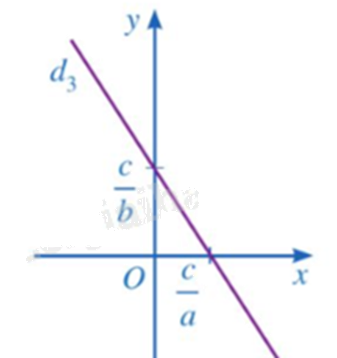
Mỗi nghiệm của phương trình \(ax + by = c\left( {a \ne 0,b \ne 0} \right)\) được biểu diễn bởi một điểm nằm trên đường thẳng \({d_3}:y = - \frac{a}{b}x + \frac{c}{b}\).
Phương trình bậc nhất hai ẩn là phương trình có dạng tổng quát: ax + by = c, trong đó a, b, c là các số thực và a, b không đồng thời bằng 0. Đây là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 9, là nền tảng cho việc học các kiến thức nâng cao hơn về hệ phương trình và hình học phân tích.
Tập nghiệm của phương trình bậc nhất hai ẩn là tập hợp tất cả các cặp số (x; y) thỏa mãn phương trình đó. Trên mặt phẳng tọa độ, tập nghiệm này là một đường thẳng.
Xét phương trình 2x + y = 4.
Vẽ đường thẳng đi qua hai điểm A(0; 4) và B(1; 2), ta được đồ thị của phương trình 2x + y = 4.
Nếu a = 0, phương trình trở thành by = c (với b ≠ 0). Khi đó, phương trình có nghiệm duy nhất y = c/b và tập nghiệm là đường thẳng song song với trục Oy.
Nếu b = 0, phương trình trở thành ax = c (với a ≠ 0). Khi đó, phương trình có nghiệm duy nhất x = c/a và tập nghiệm là đường thẳng song song với trục Ox.
Việc biểu diễn hình học nghiệm của phương trình bậc nhất hai ẩn giúp chúng ta hiểu rõ hơn về mối liên hệ giữa đại số và hình học. Thông qua đồ thị, chúng ta có thể dễ dàng nhận biết các tính chất của phương trình, chẳng hạn như vị trí của đường thẳng so với các trục tọa độ, độ dốc của đường thẳng, và các điểm đặc biệt trên đường thẳng.
Để củng cố kiến thức, hãy thực hành giải các bài tập sau:
Việc nắm vững cách biểu diễn hình học nghiệm của phương trình bậc nhất hai ẩn là rất quan trọng trong chương trình Toán 9. Hy vọng bài học này đã giúp bạn hiểu rõ hơn về kiến thức này và tự tin hơn trong việc giải các bài toán liên quan. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.