Bài viết này sẽ hướng dẫn chi tiết cách giải các bài toán liên quan đến việc tìm điều kiện của tham số trong phương trình đường thẳng ax + by = c, đặc biệt dành cho học sinh lớp 9. Chúng ta sẽ cùng nhau khám phá các phương pháp tiếp cận, các ví dụ minh họa và các lưu ý quan trọng để nắm vững kiến thức này.
Nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho việc học tập các môn học liên quan đến toán học ở các lớp trên.
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng
\(ax + by = c\)
trong đó a, b và c là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)).
Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của phương trình \(ax + by = c\).
Phương trình bậc nhất hai ẩn \(ax + by = c\) luôn luôn có vô số nghiệm.
Để xác định cặp số \(\left( {{x_0};{y_0}} \right)\) có là nghiệm của phương trình \(ax + by = c\) không, ta thay \(x = {x_0}\) và \(y = {y_0}\) vào phương trình \(ax + by = c\):
+ Nếu \(a{x_0} + b{y_0} = c\) thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình \(ax + by = c\).
+ Nếu \(a{x_0} + b{y_0} = c\) thì \(\left( {{x_0};{y_0}} \right)\) không là nghiệm của phương trình \(ax + by = c\).
- Trong mặt phẳng toạ độ Oxy, mỗi nghiệm của phương trình \(ax + by = c\) được biểu diễn bởi một điểm. Nghiệm \(\left( {{x_0};{y_0}} \right)\) được biểu diễn bởi điểm có toạ độ \(\left( {{x_0};{y_0}} \right)\).
- Tất cả các nghiệm của phương trình đó được biểu diễn bởi một đường thẳng.
+ Phương trình \(ax + 0y = c\left( {a \ne 0} \right)\)
Mỗi nghiệm của phương trình \(ax + 0y = c\left( {a \ne 0} \right)\) được biểu diễn bởi điểm có toạ độ \(\left( {\frac{c}{a};{y_0}} \right)\) \(\left( {{y_0} \in \mathbb{R}} \right)\) nằm trên đường thẳng \({d_1}:x = \frac{c}{a}\). Đường thẳng \({d_1}\) là đường thẳng đi qua điểm \(\frac{c}{a}\) trên trục Ox và vuông góc với trục Ox.
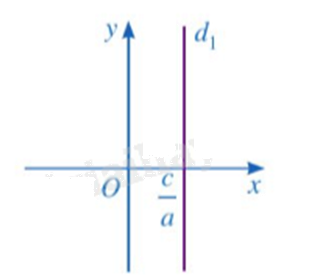
+ Phương trình \(0x + by = c\left( {b \ne 0} \right)\)
Mỗi nghiệm của phương trình \(0x + by = c\left( {b \ne 0} \right)\) được biểu diễn bởi một điểm có toạ độ \(\left( {{x_0};\frac{c}{b}} \right)\left( {{x_0} \in \mathbb{R}} \right)\) nằm trên đường thẳng \({d_2}:y = \frac{c}{b}\). Đường thẳng \({d_2}\) là đường thẳng đi qua điểm \(\frac{c}{b}\) trên trục Oy và vuông góc với trục Oy.
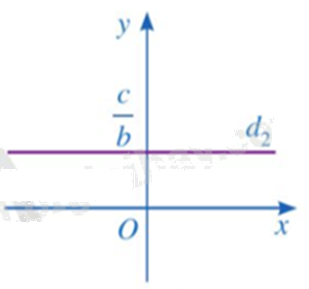
+ Phương trình \(ax + by = c\left( {a \ne 0,b \ne 0} \right)\)
Mỗi nghiệm của phương trình \(ax + by = c\left( {a \ne 0,b \ne 0} \right)\) được biểu diễn bởi một điểm nằm trên đường thẳng \({d_3}:y = - \frac{a}{b}x + \frac{c}{b}\).
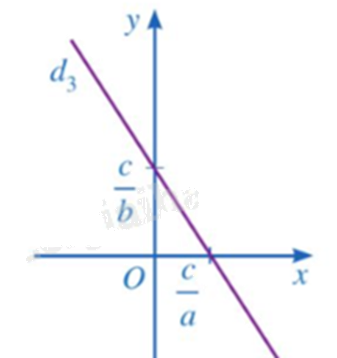
- Trường hợp 1: Nếu \(a \ne 0\) và \(b = 0\) thì phương trình đường thẳng d: ax + by = c có dạng: \(x = \frac{c}{a}\) suy ra đường thẳng d song song hoặc trùng với Oy (trục tung của trục toạ độ)
- Trường hợp 2: Nếu a = 0 và b ≠ 0 thì phương trình đường thẳng d: ax + by = c có dạng: \(y = \frac{c}{b}\) suy ra đường thẳng d song song hoặc trùng với Ox (trục hoành của trục toạ độ)
- Trường hợp 3: Đường thẳng d: \(ax + by = c\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \(a{x_0} + b{y_0} = c\).
Trong chương trình Toán 9, phương trình đường thẳng ax + by = c là một khái niệm quan trọng. Trong đó, a, b, c là các hệ số và x, y là các biến số. Việc hiểu rõ ý nghĩa của các hệ số này và cách xác định đường thẳng dựa trên phương trình là bước đầu tiên để giải quyết các bài toán liên quan.
Điều kiện tham số trong bài toán này thường liên quan đến việc đường thẳng ax + by = c thỏa mãn một điều kiện nào đó được đề bài đưa ra. Ví dụ, đường thẳng đi qua một điểm cho trước, song song với một đường thẳng khác, hoặc tạo một góc nhất định với một đường thẳng khác. Việc tìm điều kiện của tham số a, b, hoặc c để thỏa mãn các điều kiện này đòi hỏi chúng ta phải vận dụng kiến thức về hình học và đại số.
Ví dụ 1: Tìm điều kiện của tham số m để đường thẳng (m-1)x + (2m+1)y = 3m đi qua điểm A(1; 1).
Giải: Thay x = 1 và y = 1 vào phương trình, ta được: (m-1) + (2m+1) = 3m. Giải phương trình này, ta tìm được m = 0.
Ví dụ 2: Tìm điều kiện của tham số k để đường thẳng 2x + ky = 5 song song với đường thẳng 4x + 6y = 1.
Giải: Áp dụng điều kiện song song, ta có: 2/4 = k/6 ≠ 5/1. Từ đó, ta tìm được k = 3.
Việc tìm điều kiện của tham số để đường thẳng ax + by = c thỏa mãn điều kiện cho trước của đề bài là một kỹ năng quan trọng trong chương trình Toán 9. Bằng cách nắm vững các phương pháp và luyện tập thường xuyên, bạn sẽ có thể giải quyết các bài toán một cách tự tin và hiệu quả. Chúc các bạn học tốt!