Bài học này sẽ hướng dẫn bạn cách tiếp cận và giải quyết các bài toán phức tạp liên quan đến tỉ lệ phần trăm bằng phương pháp lập hệ phương trình. Đây là một kỹ năng quan trọng trong chương trình Toán 9, giúp bạn rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Chúng ta sẽ cùng nhau phân tích cấu trúc bài toán, xác định ẩn số, lập hệ phương trình và tìm ra nghiệm để giải quyết bài toán một cách hiệu quả nhất.
Các bước giải bài toán bằng cách lập hệ phương trình:
Bước 1. Lập hệ phương trình:
- Chọn ẩn số (thường chọn hai ẩn số) và đặt điều kiện thích hợp cho các ẩn số;
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
- Lập hệ phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải hệ phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm tìm được của hệ phương trình, nghiệm nào thoả mãn, nghiệm nào không thoả mãn điều kiện của ẩn, rồi kết luận.
Lưu ý: \(a\% = \frac{a}{{100}}\).
Tỉ số giữa hai số a và b là \(\frac{a}{b}\).
Bước 1. Từ một phương trình của hệ, biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại của hệ để được phương trình chỉ còn chứa một ẩn.
Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ đã cho.
Lưu ý: Tuỳ theo hệ phương trình, ta có thể lựa chọn cách biểu diễn x theo y hoặc y theo x.
Bước 1. Đưa hệ phương trình đã cho về hệ phương trình có hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau bằng cách nhân hai vế của một phương trình với một số thích hợp (khác 0).
Bước 2. Cộng hay trừ từng vế của hai phương trình trong hệ để được phương trình chỉ còn chứa một ẩn.
Bước 3. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.
Ta sử dụng loại máy tính cầm tay (MTCT) có chức năng này (có phím MODE/MENU). Dưới đây là hướng dẫn cụ thể với máy Fx-580VNX.
Ta viết phương trình cần giải dưới dạng \(\left\{ \begin{array}{l}{a_1}x + {b_1}y = {c_1}\\{a_2}x + {b_2}y + {c_2}\end{array} \right.\).
Ví dụ: Giải hệ \(\left\{ \begin{array}{l}2x + y - 4 = 0\\ - 2x + y = 0\end{array} \right.\), ta viết nó dưới dạng \(\left\{ \begin{array}{l}2x + y = 4\\ - 2x + y = 0\end{array} \right.\).
Khi đó, ta có \({a_1} = 2\), \({b_1} = 1\), \({c_1} = 4\), \({a_2} = - 2\), \({b_2} = 1\), \({c_2} = 0\). Lần lượt thực hiện các bước sau:
Bước 1. Vào chức năng hệ hai phương trình bậc nhất hai ẩn bằng cách nhấn MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).
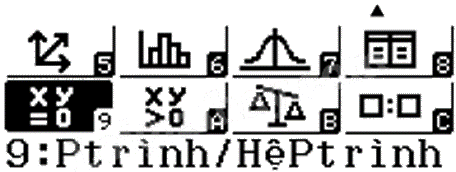
Bấm phím 1 để chọn Simul Equation (hệ phương trình).
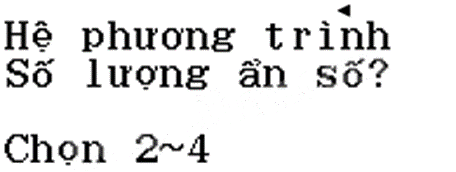
Cuối cùng, bấm phím 2 để giải hệ hai phương trình bậc nhất
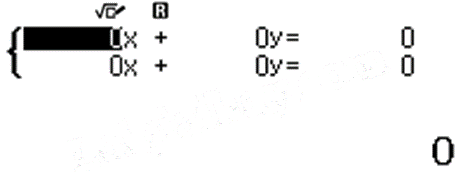
Bước 2. Ta nhập các hệ số \({a_1},{b_1},{c_1},{a_2},{b_2},{c_2}\) bằng cách bấm
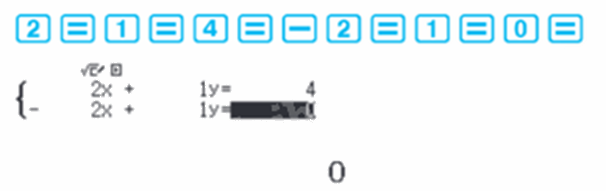
Bước 3. Sau khi nhập xong, ta bấm phím =, màn hình hiện x = 1; tiếp tục bấm =, màn hình hiện y = 3. Ta hiểu nghiệm của hệ phương trình là (-1;2).
Chú ý:
- Muốn xoá số vừa mới nhập thì bấm phím AC, muốn thay đổi số đã nhập ở vị trí nào đó thì di chuyển con trỏ đến vị trí đó rồi nhập số mới.
- Bấm phím ▲ hay ▼ để chuyển hiển thị các giá trị của x và y trong kết quả.
- Nếu máy báo Infinite Solution thì hệ phương trình đã cho có vô số nghiệm.
Nếu máy báo No Solution thì hệ phương trình đã cho vô nghiệm.
Trong chương trình Toán 9, dạng bài toán liên quan đến tỉ lệ phần trăm thường xuất hiện với nhiều hình thức khác nhau. Việc giải quyết các bài toán này đòi hỏi học sinh phải nắm vững kiến thức về tỉ lệ, phần trăm và đặc biệt là kỹ năng lập hệ phương trình bậc nhất hai ẩn. Hệ phương trình là một công cụ mạnh mẽ giúp chúng ta mô hình hóa các mối quan hệ giữa các đại lượng trong bài toán và tìm ra giá trị của các ẩn số.
Bài toán: Một cửa hàng bán hai loại gạo: gạo tẻ và gạo nếp. Giá gạo tẻ là 15.000 đồng/kg, giá gạo nếp là 20.000 đồng/kg. Trong một buổi sáng, cửa hàng bán được 50kg gạo, thu được 880.000 đồng. Hỏi cửa hàng đã bán được bao nhiêu kg gạo tẻ và bao nhiêu kg gạo nếp?
Giải:
Từ phương trình 1, ta có: x = 50 - y
Thay vào phương trình 2, ta được: 15000(50 - y) + 20000y = 880000
Giải phương trình, ta được: y = 24
Suy ra: x = 50 - 24 = 26
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Việc nắm vững phương pháp lập hệ phương trình để giải các bài toán tỉ lệ phần trăm là một kỹ năng quan trọng trong chương trình Toán 9. Hy vọng rằng bài học này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài toán một cách tự tin và hiệu quả.