Dạng toán này là một phần quan trọng trong chương trình Toán nâng cao lớp 4, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề. Bài học này sẽ cung cấp phương pháp giải chi tiết và các bài tập thực hành đa dạng để học sinh nắm vững kiến thức.
Tại giaitoan.edu.vn, chúng tôi mang đến cho học sinh một môi trường học tập trực tuyến hiệu quả, với các bài giảng được thiết kế sinh động, dễ hiểu và phù hợp với từng trình độ.
Huy và Hưng có 235 viên bi. Biết số bi của Huy bằng 2/3 số bi của Hưng ... Có hai thùng đựng 96 lít dầu, biết 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai.
Phương pháp giải: Bước 1: Vẽ sơ đồ Bước 2: Tìm tổng số phần bằng nhau Bước 3: Tìm số bé và số lớn Số bé = Tổng : số phần bằng nhau x số phần của số bé Số lớn = Tổng : số phần bằng nhau x số phần của số lớn Bước 4: Kết luận, đáp số |
Ví dụ 1: Huy và Hưng có 235 viên bi. Biết số bi của Huy bằng $\frac{2}{3}$ số bi của Hưng. Tìm số bi của Huy và Hưng?
Giải
Ta có sơ đồ:
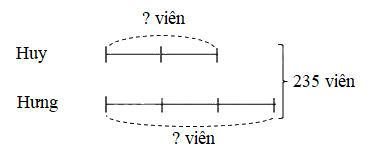
Tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Số viên bi của Huy là:
235 : 5 x 2 = 94 (viên bi)
Số viên bi của Hưng là:
235 – 94 = 141 (viên)
Đáp số: Huy: 94 viên ; Hưng: 141 viên
Ví dụ 2: Có hai thùng đựng 96 lít dầu, biết 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai. Hỏi mỗi thùng đựng bao nhiêu lít dầu?
Giải
Ta có: 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai
Hay số lít dầu ở thùng thứ nhất bằng $\frac{3}{5}$ thùng thứ hai.
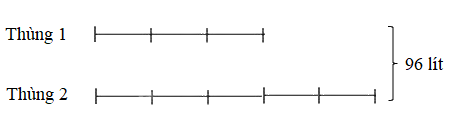
Tổng số phần bằng nhau:
3 + 5 = 8 (phần)
Số lít dầu thùng thứ nhất đựng:
96 : 8 x 3 = 36 (lít)
Số lít dầu thùng thứ hai đựng:
96 - 36 = 60 (lít)
Đáp số: Thùng thứ nhất: 36 lít; thùng thứ hai: 60 lít
Ví dụ 3: Tìm hai số tự nhiên, biết trung bình cộng của chúng là 120 và $\frac{1}{3}$ số thứ nhất bằng $\frac{1}{7}$ số thứ hai.
Giải
Tổng hai số là: 120 × 2 = 240
$\frac{1}{3}$ số thứ nhất bằng $\frac{1}{7}$ số thứ hai nên số thứ nhất bằng $\frac{3}{7}$ số thứ hai.
Ta có sơ đồ:
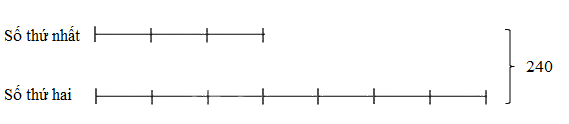
Tổng số phần bằng nhau:
3 + 7 = 10 (phần)
Số thứ nhất là:
240 : 10 x 3 = 72
Số thứ hai là:
240 – 72 = 168
Đáp số: Số thứ nhất: 72; số thứ hai: 168
Bài tập áp dụng:
Một hình chữ nhật có chu vi là 350m, chiều rộng bằng $\frac{3}{4}$ chiều dài. Tìm chiều dài, chiều rộng của hình chữ nhật đó.
Cho một số tự nhiên, biết rằng khi ta thêm vào bên phải số đó một chữ số 0 thì ta được số mới. Trung bình cộng của số mới và số cũ là 132. Tìm số đó.
Tìm hai số có tổng bằng 950. Biết rằng nếu xóa chữ số 4 ở hàng đơn vị của số lớn thì được số bé.
Trong một cái túi có tổng cộng 155 viên bi gồm 2 loại: bi xanh và bi đỏ. Biết số bi xanh nếu thêm 5 bi thì bằng $\frac{1}{4}$ số bi đỏ. Hỏi mỗi loại có bao nhiêu viên bi?
Dạng toán tìm hai số khi biết tổng và tỉ số là một trong những dạng toán quan trọng của chương trình Toán nâng cao lớp 4. Dạng toán này không chỉ giúp học sinh củng cố kiến thức về số học mà còn phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề.
Để giải bài toán tìm hai số khi biết tổng và tỉ số, chúng ta có thể áp dụng phương pháp sau:
Ví dụ 1: Tổng của hai số là 120. Số thứ nhất bằng 2/3 số thứ hai. Tìm hai số đó.
Giải:
Ví dụ 2: Hai số có tổng là 84. Tỉ số giữa hai số là 1:3. Tìm hai số đó.
Giải:
Dưới đây là một số bài tập để các em học sinh luyện tập:
Dạng toán tìm hai số khi biết tổng và tỉ số có thể được mở rộng để giải các bài toán phức tạp hơn, ví dụ như bài toán tìm ba số khi biết tổng và tỉ số của chúng. Để giải các bài toán này, chúng ta cần áp dụng linh hoạt phương pháp giải đã học và rèn luyện kỹ năng tư duy logic.
Để học tốt dạng toán này, các em học sinh cần:
Chúc các em học sinh học tốt môn Toán!