Dạng toán này là một phần quan trọng trong chương trình Toán nâng cao lớp 4, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề. Bài học này sẽ cung cấp phương pháp giải chi tiết và các bài tập thực hành đa dạng để học sinh nắm vững kiến thức.
Tại giaitoan.edu.vn, chúng tôi mang đến cho học sinh một môi trường học tập trực tuyến hiệu quả, với các bài giảng được thiết kế sinh động, dễ hiểu và phù hợp với từng trình độ.
Một trại nuôi gà có số gà mái hơn số gà trống là 345 con. Sau khi mua thêm 25 con gà trống thì số gà trống bằng 3/7 số gà mái ...
Phương pháp giải: Bước 1: Vẽ sơ đồ Bước 2: Tìm hiệu số phần bằng nhau Bước 3: Tìm số bé và số lớn Số bé = Hiệu : hiệu số phần bằng nhau x số phần của số bé Số lớn = Hiệu : hiệu số phần bằng nhau x số phần của số lớn Bước 4: Kết luận, đáp số |
Ví dụ 1: Một hình chữ nhật có chiều dài hơn chiều rộng 12m . Tìm chiều dài, chiều rộng của hình đó, biết chiều dài bằng $\frac{7}{4}$ chiều rộng.
Giải
Ta có sơ đồ:
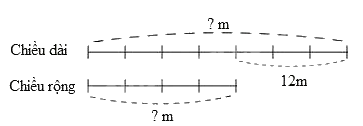
Hiệu số phần bằng nhau là:
7 – 4 = 3 (phần)
Chiều dài hình chữ nhật là:
12 : 3 x 7 = 28 (m)
Chiều rộng hình chữ nhật là:
28 – 12 = 16 (m)
Đáp số: Chiều dài: 28 m
Chiều rộng: 16 m
Ví dụ 2: Một trại nuôi gà có số gà mái hơn số gà trống là 345 con. Sau khi mua thêm 25 con gà trống thì số gà trống bằng$\frac{3}{7}$ số gà mái. Tìm tổng số gà ban đầu.
Giải
Sau khi mua thêm 25 con gà trống thì gà mái nhiều hơn gà trống số con là:
345 – 25 = 320 (con)
Hiệu số phần bằng nhau là:
7 – 3 = 4 (phần)
Số con gà trống sau khi mua thêm là:
320 : 4 x 3 = 240 (con)
Số con gà trống ban đầu là:
240 – 25 = 215 (con)
Số gà mái ban đầu là:
215 + 345 = 560 (con)
Tổng số gà ban đầu là:
215 + 560 = 775 (con)
Đáp số: 775 con
Ví dụ 3: Một người bán được số gạo tẻ nhiều hơn số gạo nếp là 20 kg. Trong đó $\frac{1}{5}$ số gạo tẻ bằng $\frac{1}{3}$ số gạo nếp. Hỏi người đó bán được bao nhiêu kg gạo mỗi loại?
Giải
Ta có $\frac{1}{5}$ số gạo tẻ bằng $\frac{1}{3}$ số gạo nếp nên số gạo tẻ bằng $\frac{5}{3}$ số gạo nếp.
Ta có sơ đồ:
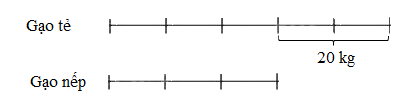
Hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Số kg gạo tẻ bán được là:
20 : 2 x 5 = 50 (kg)
Số kg gạo nếp bán được là:
50 – 20 = 30 (kg)
Đáp số: Gạo tẻ: 50 kg ; gạo nếp 30 kg
Bài tập áp dụng:
Tìm hai số có hiệu bằng 1134, biết rằng khi thêm một chữ số 0 vào bên phải số bé thì được số lớn.
Tìm hai số, biết số lớn có 3 chữ số, gấp 9 lần số bé và nếu xóa đi chữ số 4 ở hàng trăm của số lớn thì được số bé.
Biết hiện nay bố 32 tuổi, con 4 tuổi. Hỏi bao nhiêu năm nữa bố gấp 5 lần tuổi con?
Tổ 1 trồng nhiều hơn tổ 2 là 22 cây. Nếu tổ 1 trồng thêm 2 cây và tổ 2 bớt đi 3 cây thì tỉ số cây trồng được của hai tổ là $\frac{7}{4}$. Tìm số cây mỗi tổ trồng được.
Dạng toán này thường xuất hiện trong các bài kiểm tra và thi học sinh giỏi Toán lớp 4. Để giải quyết dạng bài này, học sinh cần nắm vững kiến thức về tỉ số và hiệu của hai số. Dưới đây là hướng dẫn chi tiết và các ví dụ minh họa.
1. Tỉ số của hai số: Tỉ số của hai số a và b (b ≠ 0) là thương của phép chia a cho b, được viết là a : b hoặc a/b. Ví dụ: Tỉ số của 12 và 4 là 12 : 4 = 3.
2. Hiệu của hai số: Hiệu của hai số a và b là kết quả của phép trừ a - b. Ví dụ: Hiệu của 15 và 7 là 15 - 7 = 8.
3. Mối quan hệ giữa tỉ số và hiệu: Khi biết tỉ số và hiệu của hai số, ta có thể tìm được hai số đó bằng cách sử dụng các phương pháp đại số đơn giản.
Để giải bài toán tìm hai số khi biết hiệu và tỉ số, ta thường sử dụng phương pháp sau:
Ví dụ 1: Tìm hai số, biết rằng tỉ số của chúng là 4 : 5 và hiệu của chúng là 12.
Giải:
Ví dụ 2: Hai số có tỉ số là 2 : 3 và hiệu của chúng là 25. Tìm hai số đó.
Giải:
Dưới đây là một số bài tập để bạn luyện tập:
Dạng toán tìm hai số khi biết hiệu và tỉ số là một dạng toán quan trọng trong chương trình Toán nâng cao lớp 4. Việc nắm vững phương pháp giải và luyện tập thường xuyên sẽ giúp học sinh tự tin giải quyết các bài toán tương tự.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về dạng toán này và đạt kết quả tốt trong học tập.