Dạng bài tập này là một phần quan trọng trong chương trình Toán nâng cao lớp 4, giúp học sinh rèn luyện kỹ năng giải toán phức tạp hơn. Bài toán tổng – hiệu có hiệu ẩn đòi hỏi học sinh phải phân tích đề bài một cách cẩn thận để xác định đúng các đại lượng và mối quan hệ giữa chúng.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp học sinh nắm vững phương pháp giải quyết dạng bài này.
An và Bình có 70 viên bi, biết rằng nếu Bình có thêm 16 viên bi thì hai bạn có số bi bằng nhau. Hai bao gạo cân nặng tổng cộng 147kg, biết rằng nếu lấy ra ở bao gạo thứ nhất 5kg và bao gạo thứ hai 22kg thì số gạo còn lại ở hai bao gạo bằng nhau
Phương pháp giải: Cách 1: Số lớn = (tổng + hiệu) : 2 Số bé = Số lớn – hiệu = Tổng – số lớn Cách 2: Số bé = (tổng – hiệu) : 2 Số lớn = Số bé + hiệu = Tổng – số bé |
Ví dụ 1: An và Bình có 70 viên bi, biết rằng nếu Bình có thêm 16 viên bi thì hai bạn có số bi bằng nhau. Hỏi ban đầu mỗi bạn có bao nhiêu bi?
Giải
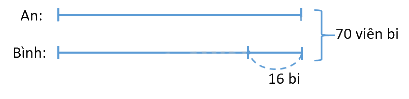
Số bi của An là:
(70 + 16) : 2 = 43 (viên bi)
Số bi của Bình là:
43 – 16 = 27 (viên bi)
Đáp số: An: 43 viên bi
Bình: 27 viên bi
Ví dụ 2: Hai bao gạo cân nặng tổng cộng 147kg, biết rằng nếu lấy ra ở bao gạo thứ nhất 5kg và bao gạo thứ hai 22kg thì số gạo còn lại ở hai bao gạo bằng nhau. Hỏi mỗi bao có bao nhiêu ki-lô-gam gạo?
Giải
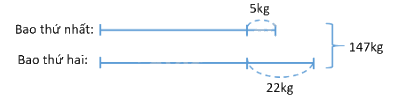
Bao thứ hai nhiều hơn bao thứ nhất số kg là:
22 – 5 = 17 (kg)
Số kg gạo ở bao thứ nhất là:
(147 – 17) : 2 = 65 (kg)
Số kg gạo ở bao thứ hai là:
65 + 17 = 82 (kg)
Đáp số: Bao thứ nhất: 65kg
Bao thứ hai: 82kg
Ví dụ 3: Tìm hai số lẻ có tổng bằng 176, biết rằng ở giữa chúng còn có 4 số lẻ.
Giải
Hai số lẻ cần tìm và có số 4 số lẻ ở giữa thì ta được 6 số lẻ liên tiếp.
Hai số lẻ liên tiếp hơn kém nhau 2 đơn vị. Vậy hiệu của hai số lẻ cần tìm là:
2 x (6 – 1) = 10
Số bé cần tìm là:
(176 – 10) : 2 = 83
Số lớn cần tìm là:
176 – 83 = 93
Đáp số:Số bé: 83 ; số lớn: 93
Bài tập áp dụng:
Hai hộp bi có tổng cộng 155 viên bi, biết rằng nếu thêm vào hộp bi thứ nhất 8 viên bi và thêm vào hộp thứ hai 17 viên bi thì hai hộp có số bi bằng nhau. Hỏi mỗi hộp có bao nhiêu viên bi?
Tìm hai số có tổng bằng 412, biết rằng nếu thêm một chữ số 3 vào bên trái số bé thì ta được số lớn.
Hai người thợ dệt được 270 m vải. Nếu người thứ nhất dệt thêm 12m và người thứ hai dệt thêm 8 m thì người thứ nhất sẽ dệt nhiều hơn người thứ hai 10 m. Hỏi mỗi người đã dệt được bao nhiêu mét vải?
Dạng bài toán tổng – hiệu có hiệu ẩn là một trong những dạng toán nâng cao thường gặp ở lớp 4. Đây là dạng toán đòi hỏi học sinh không chỉ nắm vững kiến thức về tổng, hiệu mà còn phải có khả năng phân tích đề bài một cách linh hoạt để tìm ra mối liên hệ ẩn giữa các đại lượng. Bài viết này sẽ cung cấp một cái nhìn tổng quan về dạng toán này, cùng với các phương pháp giải chi tiết và các bài tập ví dụ minh họa.
Bài toán tổng – hiệu có hiệu ẩn là bài toán trong đó tổng và hiệu của hai số được cho trước, nhưng hiệu của hai số đó không được nêu trực tiếp mà được ẩn chứa trong các thông tin khác của đề bài. Để giải quyết dạng bài toán này, học sinh cần:
Có nhiều phương pháp khác nhau để giải bài toán tổng – hiệu có hiệu ẩn, tùy thuộc vào từng dạng bài cụ thể. Dưới đây là một số phương pháp phổ biến:
Đây là phương pháp trực quan và dễ hiểu, đặc biệt phù hợp với học sinh lớp 4. Học sinh vẽ sơ đồ để biểu diễn mối quan hệ giữa các đại lượng, từ đó dễ dàng xác định tổng và hiệu của hai số cần tìm.
Phương pháp này thường được sử dụng khi hiệu ẩn được thể hiện qua một phép toán nào đó. Học sinh bắt đầu từ kết quả cuối cùng và thực hiện các phép toán ngược lại để tìm ra hiệu ẩn.
Trong một số trường hợp, học sinh có thể giả thiết một giá trị tạm thời cho một trong hai số, sau đó kiểm tra xem giả thiết đó có thỏa mãn các điều kiện của đề bài hay không. Nếu không, học sinh điều chỉnh giả thiết cho đến khi tìm được đáp án đúng.
Một cửa hàng có một số gạo. Sau khi bán đi 25kg gạo, số gạo còn lại là 15kg. Hỏi ban đầu cửa hàng có bao nhiêu kg gạo?
Giải:
Số gạo ban đầu của cửa hàng là: 25kg + 15kg = 40kg
Nhận xét: Bài toán này có thể được giải bằng cách cộng số gạo đã bán và số gạo còn lại.
Hai số có tổng là 80. Nếu tăng số bé thêm 12 đơn vị thì hai số bằng nhau. Tìm hai số đó.
Giải:
Hiệu của hai số là: 12
Số bé là: (80 - 12) : 2 = 34
Số lớn là: 80 - 34 = 46
Nhận xét: Bài toán này yêu cầu học sinh tìm ra hiệu ẩn bằng cách phân tích mối quan hệ giữa hai số.
Hy vọng với những kiến thức và phương pháp giải được trình bày trong bài viết này, các em học sinh lớp 4 sẽ tự tin hơn khi đối mặt với dạng bài toán tổng – hiệu có hiệu ẩn. Chúc các em học tập tốt!