Dạng bài tập này là một phần quan trọng trong chương trình Toán nâng cao lớp 4, giúp học sinh rèn luyện kỹ năng giải toán và tư duy logic. Bài tập tập trung vào việc tìm hiểu mối quan hệ giữa các số và trung bình cộng, từ đó giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, giúp học sinh nắm vững kiến thức và tự tin giải quyết các bài toán thuộc dạng này.
An có 24 cái kẹo, Bình có 28 cái kẹo .... Lan có 30 viên kẹo, Bình có 12 viên kẹo
Ví dụ 1: An có 24 cái kẹo, Bình có 28 cái kẹo. Cường có số cái kẹo bằng trung bình cộng của 3 bạn. hỏi Cường có bao nhiêu cái kẹo?
Giải
Ta có sơ đồ:
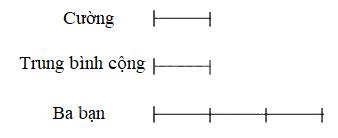
Ta thấy: Số kẹo của An và Bình ứng với 2 phần
Số kẹo của Cường là (24 + 28) : 2 = 26 (cái kẹo)
Đáp số: 26 cái kẹo
Ví dụ 2: Lan có 30 viên kẹo, Bình có 12 viên kẹo. Hoa có số viên kẹo lớn hơn trung bình cộng của cả ba bạn là 4 viên. Hỏi Hoa có bao nhiêu viên kẹo?
Giải
Ta có sơ đồ:
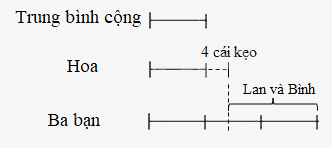
Số kẹo của Lan và Bình là 30 + 12 = 42 (cái kẹo)
Trung bình cộng số kẹo của ba bạn là (42 + 4) : 2 = 23 (cái kẹo)
Số kẹo của Hoa là 23 + 4 = 27 (cái kẹo)
Đáp số: 27 cái kẹo
Ví dụ 3: Khánh có 20 viên bi, Bảo có 31 viên bi. Nam có số bi ít hơn trung bình cộng của cả ba bạn là 5 viên bi. Hỏi Nam có bao nhiêu viên bi?
Giải
Ta có sơ đồ:
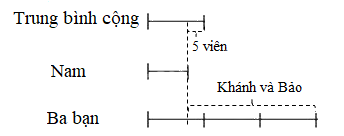
Số bi của Khánh và Bảo là: 20 + 31 = 51 (viên)
Trung bình cộng số bi của ba bạn là (51 – 5) : 2 = 23 (viên)
Bạn Nam có số viên bi là:
23 – 5 = 18 (viên)
Đáp số: 18 viên bi
Bài tập áp dụng:
Hải có 14 cái nhãn vở, Lâm có 20 cái nhãn vở. Số nhãn vở của Hà bằng trung bình cộng số nhãn vở của cả ba bạn. Hỏi Hà có bao nhiêu cái nhãn vở?
Số thứ nhất là 98, số thứ hai gấp 2 lần số thứ nhất. Số thứ ba bằng trung bình cộng của ba số. Tìm số thứ ba?
Thùng thứ nhất có 50 lít dầu, thùng thứ hai có 37 lít dầu. Thùng thứ ba có nhiều hơn trung bình cộng số dầu của cả ba thùng là 9 lít dầu. Hỏi thùng thứ ba có bao nhiêu lít dầu?
Túi kẹo thứ nhất có 25 viên, túi thứ hai nhiều hơn túi thứ nhất 7 viên kẹo. Túi thứ ba ít hơn trung bình cộng số kẹo của cả ba túi là 3 viên kẹo. Hỏi túi thứ ba có bao nhiêu viên kẹo?
Dạng bài toán này thường xuất hiện trong các đề thi Toán nâng cao lớp 4 và đòi hỏi học sinh phải nắm vững kiến thức về trung bình cộng và các mối quan hệ giữa các số. Để giải quyết hiệu quả, học sinh cần hiểu rõ các khái niệm cơ bản và áp dụng linh hoạt các công thức.
Trung bình cộng của một tập hợp các số là tổng của các số đó chia cho số lượng các số trong tập hợp. Công thức tính trung bình cộng:
Trung bình cộng = (Tổng các số) / (Số lượng các số)
Để tìm số lượng các số, ta nhân trung bình cộng với số lượng các số. Ví dụ: Nếu trung bình cộng của 3 số là 10, thì tổng của 3 số đó là 3 x 10 = 30.
Đây là dạng bài toán cơ bản nhất, học sinh chỉ cần áp dụng công thức để tính trung bình cộng.
Trong dạng bài này, một số nhỏ hơn trung bình cộng của một tập hợp các số. Để giải, ta cần tìm trung bình cộng, sau đó tìm số nhỏ hơn đó.
Tương tự như bài toán ít hơn, nhưng số cần tìm lại lớn hơn trung bình cộng.
Một số trong tập hợp bằng trung bình cộng của cả tập hợp. Dạng bài này thường yêu cầu học sinh suy luận và tìm ra mối liên hệ giữa các số.
Để giải quyết các bài toán thuộc dạng này, học sinh có thể áp dụng các bước sau:
Ví dụ 1: Trung bình cộng của ba số là 15. Số thứ nhất là 10, số thứ hai là 20. Tìm số thứ ba.
Giải:
Tổng của ba số là: 15 x 3 = 45
Số thứ ba là: 45 - 10 - 20 = 15
Ví dụ 2: Năm bạn học sinh có chiều cao trung bình là 1m40. Bốn bạn có chiều cao lần lượt là 1m35, 1m45, 1m42, 1m38. Tính chiều cao của bạn thứ năm.
Giải:
Tổng chiều cao của năm bạn là: 1m40 x 5 = 7m
Tổng chiều cao của bốn bạn là: 1m35 + 1m45 + 1m42 + 1m38 = 5m60
Chiều cao của bạn thứ năm là: 7m - 5m60 = 1m40
Dưới đây là một số bài tập để học sinh luyện tập:
Để học tốt dạng bài toán này, học sinh cần:
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn khi đối mặt với các bài toán thuộc Dạng 3: Bài toán ít hơn, nhiều hơn hoặc bằng trung bình cộng Toán nâng cao lớp 4.