Giaitoan.edu.vn xin giới thiệu bộ đề thi thử vào lớp 6 môn Toán dành cho học sinh có mong muốn ôn luyện và làm quen với cấu trúc đề thi của các trường chuyên, đặc biệt là trường chuyên Ngoại ngữ. Đề thi số 1 này được biên soạn theo sát chương trình học và có độ khó phù hợp với trình độ học sinh.
Mục tiêu của đề thi là giúp học sinh rèn luyện kỹ năng giải toán, tư duy logic và làm quen với áp lực thời gian trong phòng thi. Đồng thời, đề thi cũng là công cụ đánh giá năng lực hiện tại của học sinh, từ đó có kế hoạch ôn tập phù hợp.
Mỗi ngày Hoa đều đi đến trường bằng xe bus ... Ba bạn Uy, Minh và Sáng cùng chia nhau một số kẹo ....
ĐỀ THI THỬ VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM 2024
MÔN: TOÁN
Đề số 1
Nguồn: Sưu tầm
I. TRẮC NGHIỆM
Câu 1. Cho hai số tự nhiên có tổng là 370. Nếu số bé tăng thêm 20 đơn vị và số lớn giảm đi 10 đơn vị thì số lớn hơn số bé là 50 đơn vị. Số lớn là:
A. 205 | B. 210 | C. 215 | D. 225 |
Câu 2. Một bể nước hình hộp chữ nhật có chiều cao là 1,5m, chiều dài là 26dm và chiều rộng là 170 cm. Biết lượng nước trong bế đầy đến 80% bể, thể tích lượng nước trong bề bằng
A. 6630 lít | B. 5304 lít | C. 8287,5 lít | D. 6580 lít |
Câu 3. Mỗi ngày Hoa đều đi đến trường bằng xe bus. Trường của Hoa vào học từ 7 giờ 30 phút sáng, tuy nhiên do thời tiết trở lạnh gần đây, nhà trường đã dời giờ vào học muộn 15 phút. Từ nhà Hoa đi bộ ra bến xe bus mất 5 phút và cần thêm 20 phút nữa để xe bus đến được trường. Xe bus cứ 15 phút sẽ có một chuyển, chuyến xe đầu tiên sẽ đến nhà Hoa vào lúc 6h50 phút. Hỏi Hòa phải xuất phát từ nhà muộn nhất là mấy giờ để có thể đến trưởng đúng giờ?
A. 7 giờ 05 phút | B. 7 giờ 10 phút | C. 7 giờ 15 phút | D. 7 giờ 20 phút |
Câu 4. Ba bạn Uy, Minh và Sáng cùng chia nhau một số kẹo. Số kẹo của Uy bằng $\frac{1}{2}$ số kẹo của hai bạn còn lại. Số kẹo của Minh bằng $\frac{1}{2}$ số kẹo của Uy. Tỉ số kẹo giữa Uy và Sáng bằng:
A. 2 : 3 B. 3 : 2 C. 2 : 1 D. 3 : 1
Câu 5. Cho hình sau. Biết hình vuông to có độ dài cạnh là 10 cm, diện tích phần tô đậm bằng
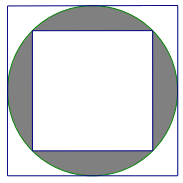
A. 25 cm2 | B. 28,5 cm2 | C. 39,25 cm2 | D. 78,5 cm2 |
II. TỰ LUẬN
Câu 1. Một chiếc cano đi xuôi dòng từ A đến B, nghỉ tại B 30 phút rồi đi ngược dòng từ B về A hết tổng cộng là 5 tiếng đồng hồ. Biết vận tốc cano khi nước lặng là 18km/h và vận tốc của dòng nước là 2km/h.
a) Tính vận tốc khi đi xuôi đòng, vận tốc khi đi ngược dòng của cano.
b) Tính khoảng cách từ A đến B.
Câu 2. Một tiệm may bán hết một khúc vải trong 4 ngày. Ngày đầu tiên, tiệm may bán được lượng vải bằng $\frac{1}{3}$ tổng lượng vải bán trong 3 ngày còn lại. Ngày thứ hai tiệm bán được gấp rưỡi lượng vài bán được trong ngày đầu tiên. Ngày thứ ba, tiệm bán được lượng vải bằng một nửa lượng vải bán được trong ngày cuối cùng. Biết ngày thứ nhất bán được hơn ngày thứ ba là 5m. Tính độ dài của cả khúc vải.
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho hai số tự nhiên có tổng là 370. Nếu số bé tăng thêm 20 đơn vị và số lớn giảm đi 10 đơn vị thì số lớn hơn số bé là 50 đơn vị. Số lớn là:
A. 205 B. 210 C. 215 D. 225
Cách giải:
Tổng 2 số lúc sau là: 370 + 20 – 10 = 380
Số lớn lúc sau: (380 + 50) : 2 = 215
Số lớn lúc đầu: 215 + 10 = 225
Đáp án: D
Câu 2. Một bể nước hình hộp chữ nhật có chiều cao là 1,5m, chiều dài là 26dm và chiều rộng là 170 cm. Biết lượng nước trong bể đầy đến 80% bể, thể tích lượng nước trong bề bằng:
A. 6630 lít B. 5304 lít C. 8287,5 lít D. 6580 lít
Cách giải:
Đổi: 1,5m = 15 dm; 170 cm = 17 dm
Thể tích của bể là: 15 x 17 x 26 = 6630 (dm3)
Thể tích nước trong bể là: 6630 x 80% = 5304(dm3) = 5304 lít
Đáp án: B
Câu 3. Mỗi ngày Hoa đều đi đến trường bằng xe bus. Trường của Hoa vào học từ 7 giờ 30 phút sáng, tuy nhiên do thời tiết trở lạnh gần đây, nhà trường đã dời giờ vào học muộn 15 phút. Từ nhà Hoa đi bộ ra bến xe bus mất 5 phút và cần thêm 20 phút nữa để xe bus đến được trường. Xe bus cứ 15 phút sẽ có một chuyển, chuyến xe đầu tiên sẽ đến nhà Hoa vào lúc 6h50 phút. Hỏi Hoa phải xuất phát từ nhà muộn nhất là mấy giờ để có thể đến trưởng đúng giờ?
A. 7 giờ 05 phút | B. 7 giờ 10 phút | C. 7 giờ 15 phút | D. 7 giờ 20 phút |
Cách giải:
Sau khi thay đổi, trường của Hoa vào học lúc: 7 giờ 30 phút + 15 phút = 7 giờ 45 phút. Thời gian xe bus di chuyển hết 20 phút, nên lúc muộn nhất Hoa lên xe là:
7 giờ 45 phút – 20 phút = 7 giờ 25 phút
Cứ 15 phút thì xe bus có một chuyến, mà chuyến đầu tiên đi qua nhà Hoa là 6 giờ 50 phút nên thời điểm các chuyến tiếp theo là 7 giờ 5 phút và 7 giờ 20 phút.
Nên chuyến xe muộn nhất Hoa có thể đi là 7 giờ 20 phút, mà nhà Hoa ra bến xe bus mất 5 phút. Nên Hoa xuất phát muộn nhất lúc: 7 giờ 20 phút – 5 phút = 7 giờ 15 phút
Đáp án: C
Câu 4. Ba bạn Uy, Minh và Sáng cùng chia nhau một số kẹo. Số kẹo của Uy bằng $\frac{1}{2}$ số kẹo của hai bạn còn lại. Số kẹo của Minh bằng $\frac{1}{2}$ số kẹo của Uy. Tỉ số kẹo giữa Uy và Sáng bằng:
A. 2 : 3 B. 3 : 2 C. 2 : 1 D. 3 : 1
Cách giải:
Số kẹo của Uy bằng $\frac{1}{2}$ số kẹo của hai bạn còn lại hay số kẹo của Uy bằng $\frac{1}{{2 + 1}} = \frac{1}{3}$ tổng số kẹo của ba bạn.
Số kẹo của Minh bằng $\frac{1}{2}$ số kẹo của Uy hay số kẹo của Minh bằng $\frac{1}{3} \times \frac{1}{2} = \frac{1}{6}$ tổng số kẹo của ba bạn.
Số kẹo của Sáng bằng 1 - $1 - \frac{1}{3} - \frac{1}{6} = \frac{1}{2}$ (tổng số kẹo)
Tỉ số kẹo của Uy và Sáng bằng $\frac{1}{3}:\frac{1}{2} = \frac{2}{3}$ hay 2 : 3
Đáp án: A
Câu 5. Cho hình sau. Biết hình vuông to có độ dài cạnh là 10 cm, diện tích phần tô đậm bằng:
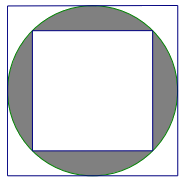
A. 25 cm2 | B. 28,5 cm2 | C. 39,25 cm2 | D. 78,5 cm2 |
Cách giải:
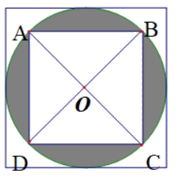
Bán kính hình tròn là: 10 : 2 = 5 (cm)
Diện tích hình tròn là 5 x 5 x 3,14 = 78,5 (cm2)
Diện tích tam giác vuông OAB là 5 x 5 : 2 = 12,5 (cm2)
Diện tích hình vuông ABCD là 12,5 x 4 = 50 (cm2)
Diện tích phần tô đậm là 78,5 – 50 = 28,5 (cm2)
Đáp án: B
II. TỰ LUẬN
Câu 1. Một chiếc cano đi xuôi dòng từ A đến B, nghỉ tại B 30 phút rồi đi ngược dòng từ B về A hết tổng cộng là 5 tiếng đồng hồ. Biết vận tốc cano khi nước lặng là 18km/h và vận tốc của dòng nước là 2km/h.
a) Tính vận tốc khi đi xuôi đòng, vận tốc khi đi ngược dòng của cano.
b) Tính khoảng cách từ A đến B.
Cách giải
a) Vận tốc của ca nô khi xuôi dòng là 18 + 2 = 20 (km/giờ)
b) Vận tốc của ca nô khi ngược dòng là 18 - 2 = 16 (km/giờ)
b) Thời gian ca nô di chuyển xuôi dòng và ngược dòng là: 5 giờ - 30 phút = 4 giờ 30 phút
Đổi: 4 giờ 30 phút = 4,5 giờ
Trên cùng quãng đường AB, thời gian và vận tốc khi xuôi, ngược dòng là hai đại lượng tỉ lệ nghịch.
Tỉ số của vận tốc khi xuôi dòng và ngược dòng là: $\frac{{20}}{{16}} = \frac{5}{4}$
Tỉ số của thời gian xuôi dòng và thời gian ngược dòng là: $\frac{4}{5}$
Thời gian ca nô xuôi dòng là 4,5 : (4 + 5) x 4 = 2 (giờ)
Quãng đường AB là: 20 x 2 = 40 (km)
Đáp số: a) 20 km/giờ; 16 km/giờ
b) 40 km
Câu 2. Một tiệm may bán hết một khúc vải trong 4 ngày. Ngày đầu tiên, tiệm may bán được lượng vải bằng $\frac{1}{3}$ tổng lượng vải bán trong 3 ngày còn lại. Ngày thứ hai tiệm bán được gấp rưỡi lượng vài bán được trong ngày đầu tiên. Ngày thứ ba, tiệm bán được lượng vải bằng một nửa lượng vải bán được trong ngày cuối cùng. Biết ngày thứ nhất bán được hơn ngày thứ ba là 5m. Tính độ dài của cả khúc vải.
Cách giải:
Ngày đầu tiên, tiệm may bán được lượng vải bằng $\frac{1}{3}$ tổng lượng vải bán trong 3 ngày còn lại.
Hay ngày thứ nhất bán được lượng vải bằng $\frac{1}{4}$ tổng lượng vải.
Lượng ngày thứ hai tiệm bán là: $\frac{1}{4} \times \frac{3}{2} = \frac{3}{8}$ (tổng lượng vải)
Lượng vải tiệm bán được trong hai ngày cuối là $1 - \frac{3}{8} - \frac{1}{4} = \frac{3}{8}$(tổng lượng vải)
Lượng vải ngày thứ ba bán được bằng $\frac{1}{2}$ lượng vải bán ngày thứ tư.
Lượng vải bán trong ngày thứ ba là $\frac{3}{8}:(1 + 2) \times 1 = \frac{1}{8}$ (tổng lượng vải)
Ngày thứ nhất bán được hơn ngày thứ ba là 5m.
Phân số chỉ 5 m vải là: $\frac{1}{4} - \frac{1}{8} = \frac{1}{8}$ (tổng lượng vải)
Độ dài của khúc vải là $5:\frac{1}{8} = 40$ (m vải)
Đáp số: 40 m vải
ĐỀ THI THỬ VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM 2024
MÔN: TOÁN
Đề số 1
Nguồn: Sưu tầm
I. TRẮC NGHIỆM
Câu 1. Cho hai số tự nhiên có tổng là 370. Nếu số bé tăng thêm 20 đơn vị và số lớn giảm đi 10 đơn vị thì số lớn hơn số bé là 50 đơn vị. Số lớn là:
A. 205 | B. 210 | C. 215 | D. 225 |
Câu 2. Một bể nước hình hộp chữ nhật có chiều cao là 1,5m, chiều dài là 26dm và chiều rộng là 170 cm. Biết lượng nước trong bế đầy đến 80% bể, thể tích lượng nước trong bề bằng
A. 6630 lít | B. 5304 lít | C. 8287,5 lít | D. 6580 lít |
Câu 3. Mỗi ngày Hoa đều đi đến trường bằng xe bus. Trường của Hoa vào học từ 7 giờ 30 phút sáng, tuy nhiên do thời tiết trở lạnh gần đây, nhà trường đã dời giờ vào học muộn 15 phút. Từ nhà Hoa đi bộ ra bến xe bus mất 5 phút và cần thêm 20 phút nữa để xe bus đến được trường. Xe bus cứ 15 phút sẽ có một chuyển, chuyến xe đầu tiên sẽ đến nhà Hoa vào lúc 6h50 phút. Hỏi Hòa phải xuất phát từ nhà muộn nhất là mấy giờ để có thể đến trưởng đúng giờ?
A. 7 giờ 05 phút | B. 7 giờ 10 phút | C. 7 giờ 15 phút | D. 7 giờ 20 phút |
Câu 4. Ba bạn Uy, Minh và Sáng cùng chia nhau một số kẹo. Số kẹo của Uy bằng $\frac{1}{2}$ số kẹo của hai bạn còn lại. Số kẹo của Minh bằng $\frac{1}{2}$ số kẹo của Uy. Tỉ số kẹo giữa Uy và Sáng bằng:
A. 2 : 3 B. 3 : 2 C. 2 : 1 D. 3 : 1
Câu 5. Cho hình sau. Biết hình vuông to có độ dài cạnh là 10 cm, diện tích phần tô đậm bằng
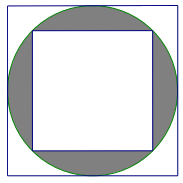
A. 25 cm2 | B. 28,5 cm2 | C. 39,25 cm2 | D. 78,5 cm2 |
II. TỰ LUẬN
Câu 1. Một chiếc cano đi xuôi dòng từ A đến B, nghỉ tại B 30 phút rồi đi ngược dòng từ B về A hết tổng cộng là 5 tiếng đồng hồ. Biết vận tốc cano khi nước lặng là 18km/h và vận tốc của dòng nước là 2km/h.
a) Tính vận tốc khi đi xuôi đòng, vận tốc khi đi ngược dòng của cano.
b) Tính khoảng cách từ A đến B.
Câu 2. Một tiệm may bán hết một khúc vải trong 4 ngày. Ngày đầu tiên, tiệm may bán được lượng vải bằng $\frac{1}{3}$ tổng lượng vải bán trong 3 ngày còn lại. Ngày thứ hai tiệm bán được gấp rưỡi lượng vài bán được trong ngày đầu tiên. Ngày thứ ba, tiệm bán được lượng vải bằng một nửa lượng vải bán được trong ngày cuối cùng. Biết ngày thứ nhất bán được hơn ngày thứ ba là 5m. Tính độ dài của cả khúc vải.
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho hai số tự nhiên có tổng là 370. Nếu số bé tăng thêm 20 đơn vị và số lớn giảm đi 10 đơn vị thì số lớn hơn số bé là 50 đơn vị. Số lớn là:
A. 205 B. 210 C. 215 D. 225
Cách giải:
Tổng 2 số lúc sau là: 370 + 20 – 10 = 380
Số lớn lúc sau: (380 + 50) : 2 = 215
Số lớn lúc đầu: 215 + 10 = 225
Đáp án: D
Câu 2. Một bể nước hình hộp chữ nhật có chiều cao là 1,5m, chiều dài là 26dm và chiều rộng là 170 cm. Biết lượng nước trong bể đầy đến 80% bể, thể tích lượng nước trong bề bằng:
A. 6630 lít B. 5304 lít C. 8287,5 lít D. 6580 lít
Cách giải:
Đổi: 1,5m = 15 dm; 170 cm = 17 dm
Thể tích của bể là: 15 x 17 x 26 = 6630 (dm3)
Thể tích nước trong bể là: 6630 x 80% = 5304(dm3) = 5304 lít
Đáp án: B
Câu 3. Mỗi ngày Hoa đều đi đến trường bằng xe bus. Trường của Hoa vào học từ 7 giờ 30 phút sáng, tuy nhiên do thời tiết trở lạnh gần đây, nhà trường đã dời giờ vào học muộn 15 phút. Từ nhà Hoa đi bộ ra bến xe bus mất 5 phút và cần thêm 20 phút nữa để xe bus đến được trường. Xe bus cứ 15 phút sẽ có một chuyển, chuyến xe đầu tiên sẽ đến nhà Hoa vào lúc 6h50 phút. Hỏi Hoa phải xuất phát từ nhà muộn nhất là mấy giờ để có thể đến trưởng đúng giờ?
A. 7 giờ 05 phút | B. 7 giờ 10 phút | C. 7 giờ 15 phút | D. 7 giờ 20 phút |
Cách giải:
Sau khi thay đổi, trường của Hoa vào học lúc: 7 giờ 30 phút + 15 phút = 7 giờ 45 phút. Thời gian xe bus di chuyển hết 20 phút, nên lúc muộn nhất Hoa lên xe là:
7 giờ 45 phút – 20 phút = 7 giờ 25 phút
Cứ 15 phút thì xe bus có một chuyến, mà chuyến đầu tiên đi qua nhà Hoa là 6 giờ 50 phút nên thời điểm các chuyến tiếp theo là 7 giờ 5 phút và 7 giờ 20 phút.
Nên chuyến xe muộn nhất Hoa có thể đi là 7 giờ 20 phút, mà nhà Hoa ra bến xe bus mất 5 phút. Nên Hoa xuất phát muộn nhất lúc: 7 giờ 20 phút – 5 phút = 7 giờ 15 phút
Đáp án: C
Câu 4. Ba bạn Uy, Minh và Sáng cùng chia nhau một số kẹo. Số kẹo của Uy bằng $\frac{1}{2}$ số kẹo của hai bạn còn lại. Số kẹo của Minh bằng $\frac{1}{2}$ số kẹo của Uy. Tỉ số kẹo giữa Uy và Sáng bằng:
A. 2 : 3 B. 3 : 2 C. 2 : 1 D. 3 : 1
Cách giải:
Số kẹo của Uy bằng $\frac{1}{2}$ số kẹo của hai bạn còn lại hay số kẹo của Uy bằng $\frac{1}{{2 + 1}} = \frac{1}{3}$ tổng số kẹo của ba bạn.
Số kẹo của Minh bằng $\frac{1}{2}$ số kẹo của Uy hay số kẹo của Minh bằng $\frac{1}{3} \times \frac{1}{2} = \frac{1}{6}$ tổng số kẹo của ba bạn.
Số kẹo của Sáng bằng 1 - $1 - \frac{1}{3} - \frac{1}{6} = \frac{1}{2}$ (tổng số kẹo)
Tỉ số kẹo của Uy và Sáng bằng $\frac{1}{3}:\frac{1}{2} = \frac{2}{3}$ hay 2 : 3
Đáp án: A
Câu 5. Cho hình sau. Biết hình vuông to có độ dài cạnh là 10 cm, diện tích phần tô đậm bằng:
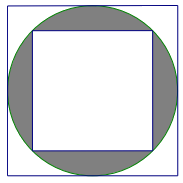
A. 25 cm2 | B. 28,5 cm2 | C. 39,25 cm2 | D. 78,5 cm2 |
Cách giải:
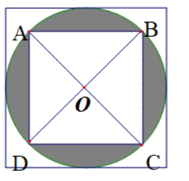
Bán kính hình tròn là: 10 : 2 = 5 (cm)
Diện tích hình tròn là 5 x 5 x 3,14 = 78,5 (cm2)
Diện tích tam giác vuông OAB là 5 x 5 : 2 = 12,5 (cm2)
Diện tích hình vuông ABCD là 12,5 x 4 = 50 (cm2)
Diện tích phần tô đậm là 78,5 – 50 = 28,5 (cm2)
Đáp án: B
II. TỰ LUẬN
Câu 1. Một chiếc cano đi xuôi dòng từ A đến B, nghỉ tại B 30 phút rồi đi ngược dòng từ B về A hết tổng cộng là 5 tiếng đồng hồ. Biết vận tốc cano khi nước lặng là 18km/h và vận tốc của dòng nước là 2km/h.
a) Tính vận tốc khi đi xuôi đòng, vận tốc khi đi ngược dòng của cano.
b) Tính khoảng cách từ A đến B.
Cách giải
a) Vận tốc của ca nô khi xuôi dòng là 18 + 2 = 20 (km/giờ)
b) Vận tốc của ca nô khi ngược dòng là 18 - 2 = 16 (km/giờ)
b) Thời gian ca nô di chuyển xuôi dòng và ngược dòng là: 5 giờ - 30 phút = 4 giờ 30 phút
Đổi: 4 giờ 30 phút = 4,5 giờ
Trên cùng quãng đường AB, thời gian và vận tốc khi xuôi, ngược dòng là hai đại lượng tỉ lệ nghịch.
Tỉ số của vận tốc khi xuôi dòng và ngược dòng là: $\frac{{20}}{{16}} = \frac{5}{4}$
Tỉ số của thời gian xuôi dòng và thời gian ngược dòng là: $\frac{4}{5}$
Thời gian ca nô xuôi dòng là 4,5 : (4 + 5) x 4 = 2 (giờ)
Quãng đường AB là: 20 x 2 = 40 (km)
Đáp số: a) 20 km/giờ; 16 km/giờ
b) 40 km
Câu 2. Một tiệm may bán hết một khúc vải trong 4 ngày. Ngày đầu tiên, tiệm may bán được lượng vải bằng $\frac{1}{3}$ tổng lượng vải bán trong 3 ngày còn lại. Ngày thứ hai tiệm bán được gấp rưỡi lượng vài bán được trong ngày đầu tiên. Ngày thứ ba, tiệm bán được lượng vải bằng một nửa lượng vải bán được trong ngày cuối cùng. Biết ngày thứ nhất bán được hơn ngày thứ ba là 5m. Tính độ dài của cả khúc vải.
Cách giải:
Ngày đầu tiên, tiệm may bán được lượng vải bằng $\frac{1}{3}$ tổng lượng vải bán trong 3 ngày còn lại.
Hay ngày thứ nhất bán được lượng vải bằng $\frac{1}{4}$ tổng lượng vải.
Lượng ngày thứ hai tiệm bán là: $\frac{1}{4} \times \frac{3}{2} = \frac{3}{8}$ (tổng lượng vải)
Lượng vải tiệm bán được trong hai ngày cuối là $1 - \frac{3}{8} - \frac{1}{4} = \frac{3}{8}$(tổng lượng vải)
Lượng vải ngày thứ ba bán được bằng $\frac{1}{2}$ lượng vải bán ngày thứ tư.
Lượng vải bán trong ngày thứ ba là $\frac{3}{8}:(1 + 2) \times 1 = \frac{1}{8}$ (tổng lượng vải)
Ngày thứ nhất bán được hơn ngày thứ ba là 5m.
Phân số chỉ 5 m vải là: $\frac{1}{4} - \frac{1}{8} = \frac{1}{8}$ (tổng lượng vải)
Độ dài của khúc vải là $5:\frac{1}{8} = 40$ (m vải)
Đáp số: 40 m vải
Việc chuẩn bị cho kỳ thi tuyển sinh vào lớp 6, đặc biệt là các trường chuyên như trường chuyên Ngoại ngữ, đòi hỏi sự đầu tư nghiêm túc và có phương pháp. Đề thi thử đóng vai trò quan trọng trong quá trình ôn luyện, giúp học sinh làm quen với dạng đề, rèn luyện kỹ năng và đánh giá năng lực bản thân. Bài viết này sẽ cung cấp thông tin chi tiết về đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 1), bao gồm cấu trúc đề thi, nội dung kiến thức, hướng dẫn giải và các lưu ý quan trọng.
Đề thi thử thường bao gồm các dạng bài tập sau:
Tỷ lệ phân bổ điểm giữa các dạng bài tập có thể khác nhau tùy theo từng trường, nhưng thường tập trung vào các chủ đề chính như:
Để đạt kết quả tốt trong kỳ thi tuyển sinh vào lớp 6, học sinh cần nắm vững các kiến thức sau:
Để giải đề thi thử hiệu quả, học sinh cần:
Trong quá trình làm bài thi, học sinh cần lưu ý:
Luyện đề thi thử là một bước quan trọng trong quá trình chuẩn bị cho kỳ thi tuyển sinh vào lớp 6. Việc luyện đề thường xuyên giúp học sinh:
Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 1) là một công cụ hữu ích giúp học sinh ôn luyện và chuẩn bị cho kỳ thi tuyển sinh. Hy vọng với những thông tin và hướng dẫn trên, các em học sinh sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!