Giaitoan.edu.vn cung cấp bộ đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2024 được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
Các đề thi được thiết kế bám sát cấu trúc đề thi chính thức, giúp học sinh làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề.
Đây là tài liệu ôn tập lý tưởng cho các em học sinh đang chuẩn bị bước vào kỳ thi quan trọng này.
Một đội công nhân có 42 người làm một công việc trong 85 ngày thì xong A là số có 2024 chữ số 9. B là số bé nhất thỏa mãn để tổng A + B chia hết cho 45.
ĐỀ THI VÀO LỚP 6 MÔN TOÁN THCS NGOẠI NGỮ NĂM 2024
Thời gian làm bài: 30 phút
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tổng số tuổi của hai chị em 5 năm trước là 25. Hiện nay tuổi em bằng \(\frac{2}{3}\) tuổi chị. Hỏi năm sau em bao nhiêu tuổi?
Bài 2. Một đội công nhân có 42 người làm một công việc trong 85 ngày thì xong. Sau 13 ngày thì đội có thêm 12 người nữa. Hỏi đội công nhân chỉ cần thêm bao nhiêu ngày để hoàn thành công việc?
Bài 3. Nếu có 11 gam khí CO2 thì điều chế được 8 gam khí O2. Nếu có 35,2 gam CO2 thì điều chế được bao nhiêu gam khí O2?
Bài 4. A là số có 2024 chữ số 9. B là số bé nhất thỏa mãn để tổng A + B chia hết cho 45. Tính tích các chữ số của B.
Bài 5. Cho hình bên dưới được tạo bởi 2 hình hộp chữ nhật có chiều dài là 4 cm, chiều rộng là 4 cm và chiều cao là 2 cm. Tính diện tích toàn phần của hình đó.
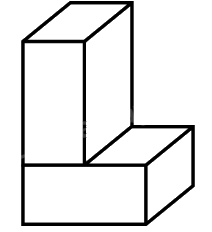
PHẦN 2. TỰ LUẬN
Bài 1. Cho tam giác ABC. Lấy điểm N trên AC sao cho NA = NC x 2 và E trên BC sao cho EC = EB x 3. Nối AE và BN cắt nhau tại I. Biết ${S_{EIB}} = 11$cm2. Hỏi:
a) $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = ?$
b) Tính SABE biết SEIB = 11 cm2
Bài 2. Chú Hải đi Hà Nội từ lúc 8h với vận tốc 35km/h. Đi một lúc thì bị hỏng xe, dừng lại sửa mất 36 phút. Đi tiếp với vận tốc 50km/h thì đến nơi đúng với giờ dự định. Biết quãng đường là 105km.
a) Chú Hải đến nơi lúc mấy giờ?
b) Chú Hải đi với vận tốc 50km/giờ trong bao lâu
c) Lúc 10h, chú Hải đi được bao nhiêu ki-lô-mét?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tổng số tuổi của hai chị em 5 năm trước là 25. Hiện nay tuổi em bằng \(\frac{2}{3}\) tuổi chị. Hỏi năm sau em bao nhiêu tuổi?
Lời giải
Tổng số tuổi hiện nay của hai chị em là:
25 + 5 + 5 = 35 (tuổi)
Ta có sơ đồ:
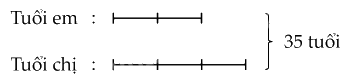
Giá trị một phần là:
35 : (2 + 3) = 7 (tuổi)
Hiện nay tuổi em là:
7 x 2 = 14 (tuổi)
Năm sau, tuổi em là:
14 + 1 = 15 (tuổi)
Đáp số: 15 tuổi
Bài 2. Một đội công nhân có 42 người làm một công việc trong 85 ngày thì xong. Sau 13 ngày thì đội có thêm 12 người nữa. Hỏi đội công nhân chỉ cần thêm bao nhiêu ngày để hoàn thành công việc?
Lời giải
Sau 13 ngày thì 42 người sẽ hoàn thành công việc còn lại sau số ngày là:
85 – 13 = 72 (ngày)
Coi 1 ngày 1 người làm được 1 phần công việc thì số phần công việc còn lại là:
42 x 72 = 3 024 (phần công việc)
Sau khi có thêm 12 người, đội công nhân có số người là:
42 + 12 = 54 (người)
Đội công nhân cần thêm số người để hoàn thành công việc là:
3 024 : 54 = 56 (ngày)
Đáp số: 56 ngày
Bài 3. Nếu có 11 gam khí CO2 thì điều chế được 8 gam khí O2. Nếu có 35,2 gam CO2 thì điều chế được bao nhiêu gam khí O2?
Lời giải
35,2 gam khí CO2 gấp 11 gam khí CO2 số lần là:
35,2 : 11 = 3,2 (lần)
35,3 gam khí CO2 điều chế được số gam khí O2 là:
8 x 3,2 = 25,6 (gam)
Đáp số: 25,6 gam
Bài 4. A là số có 2024 chữ số 9. B là số bé nhất thỏa mãn để tổng A + B chia hết cho 45. Tính tích các chữ số của B.
Lời giải
Để (A + B) chia hết cho 45 thì (A + B) chia hết cho 5 và 9.
A = $\overline {999...99} $ (2024 chữ số 9) chia hết cho 9 nên B phải là số chia hết cho 9.
B có thể là: 0, 9 , 18, 27, 36, ....
Vì A có chữ số tận cùng là 9 nên chia 5 sẽ dư 4 suy ra B chia 5 phải dư 1 thì (A + B) mới chia hết cho 5.
B chia 5 dư 1 thì B có thể là: 1, 6, 11, 16, 21, 26, 31, 36, ....
Để B bé nhất chia hết cho 9 và chia 5 dư 1 thì B = 36.
Tích các chữ số của B là: 3 x 6 = 18.
Đáp số: 18
Bài 5. Cho hình bên dưới được tạo bởi 2 hình hộp chữ nhật có chiều dài là 4 cm, chiều rộng là 4 cm và chiều cao là 2 cm. Tính diện tích toàn phần của hình đó.
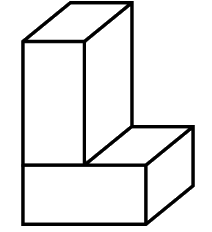
Lời giải
Diện tích toàn phần hình của một hình hộp chữ nhật là:
(4 + 4) x 2 x 2 + 4 x 4 x 2 = 64 (cm2)
Diện tích toàn phần của 2 hình hộp chữ nhật là:
64 x 2 = 128 (cm2)
Vì hình cần tính được tạo bởi 2 hình hộp chữ nhật xếp chồng lên nhau nên diện tích toàn phần hình đó bằng hiệu diện tích toàn phần của 2 hình hộp chữ nhật với 2 lần diện tích mặt tiếp xúc của 2 hình hộp chữ nhật có kích thước 4 cm x 2 cm.
Diện tích toàn phần của hình đó là:
128 – (2 x 4) x 2 = 112 (cm2)
Đáp số: 112 cm2
PHẦN 2. TỰ LUẬN
Bài 1. Cho tam giác ABC. Lấy điểm N trên AC sao cho NA = NC x 2 và E trên BC sao cho EC = EB x 3. Nối AE và BN cắt nhau tại I. Biết ${S_{EIB}} = 11$cm2. Hỏi:
a) $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = ?$
b) Tính SABE biết SEIB = 11 cm2
Lời giải
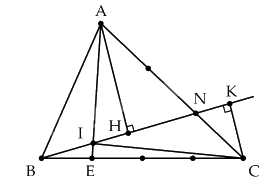
a) Từ A kẻ AH vuông góc với BN và từ C kẻ CK vuông góc với BN.
Ta có $\frac{{{S_{ABN}}}}{{{S_{CBN}}}} = \frac{{AN}}{{NC}} = \frac{2}{1}$ (Chung chiều cao từ đỉnh B)
Mà hai tam giác còn chung đáy BN nên chiều cao AH = $\frac{2}{1}$ chiều cao CK.
Ta có $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = \frac{2}{1}$ vì chung đáy BI, chiều cao AH = $\frac{2}{1}$ chiều cao CK.
b) Ta có $\frac{{{S_{BIE}}}}{{{S_{BIC}}}} = \frac{{BE}}{{BC}} = \frac{1}{4}$ (Chung chiều cao từ I)
Suy ra SBIC = 11 x 4 = 44 (cm2)
Mà $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = \frac{2}{1}$ nên SABI = 44 x 2 = 88 (cm2)
Ta có SBIE + SABI = SABE nên SABE = 88 + 11 = 99 (cm2)
Đáp số: a) $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = \frac{2}{1}$
b) SABE = 99 cm2
Bài 2. Chú Hải đi Hà Nội từ lúc 8h với vận tốc 35km/h. Đi một lúc thì bị hỏng xe, dừng lại sửa mất 36 phút. Đi tiếp với vận tốc 50km/h thì đến nơi đúng với giờ dự định. Biết quãng đường là 105km.
a) Chú Hải đến nơi lúc mấy giờ?
b) Chú Hải đi với vận tốc 50km/giờ trong bao lâu
c) Lúc 10h, chú Hải đi được bao nhiêu ki-lô-mét?
Lời giải
a) Vì chú Hải đến nơi đúng với giờ dự định, nên thời gian chú Hải đi hết quãng đường là:
105 : 35 = 3 (giờ)
Thời điểm chú Hải đến Hà Nội là:
8 giờ + 3 giờ = 11 (giờ)
b)

Gọi C là điểm mà xe dừng lại nghỉ. Khi đó quãng đường đi còn lại của xe không đổi nên vận tốc tỉ lệ nghịch với thời gian. Tỉ số vận tốc đi trên AC và đi trên BC là: $35:50 = \frac{7}{{10}}$
Tỉ số thời gian đi của xe đi trên AC và đi trên BC là: $\frac{{10}}{7}$
Hiệu thời gian mà xe đi được trên hai quãng đường là: 36 phút = $\frac{3}{5}$ giờ
Thời gian của xe đi với vận tốc 50 km/giờ là:
$\frac{3}{5}:(10 - 7) \times 7 = 1,4$ (giờ) = 1 giờ 24 phút.
c) Thời gian xe đi trên quãng đường AC là:
3 giờ - 36 phút – 1 giờ 24 phút = 1 (giờ)
Thời gian xe đi với vận tốc 50 km/giờ từ C đến lúc 10 giờ là:
10 giờ - 1 giờ - 36 phút = 24 phút = 0,4 (giờ)
Lúc 10 giờ chú Hải đi được số ki – lô- mét là:
35 x 1 + 50 x 0,4 = 55 (km)
Đáp số: a) 11 giờ
b) 1 giờ 24 phút
c) 55 km
ĐỀ THI VÀO LỚP 6 MÔN TOÁN THCS NGOẠI NGỮ NĂM 2024
Thời gian làm bài: 30 phút
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tổng số tuổi của hai chị em 5 năm trước là 25. Hiện nay tuổi em bằng \(\frac{2}{3}\) tuổi chị. Hỏi năm sau em bao nhiêu tuổi?
Bài 2. Một đội công nhân có 42 người làm một công việc trong 85 ngày thì xong. Sau 13 ngày thì đội có thêm 12 người nữa. Hỏi đội công nhân chỉ cần thêm bao nhiêu ngày để hoàn thành công việc?
Bài 3. Nếu có 11 gam khí CO2 thì điều chế được 8 gam khí O2. Nếu có 35,2 gam CO2 thì điều chế được bao nhiêu gam khí O2?
Bài 4. A là số có 2024 chữ số 9. B là số bé nhất thỏa mãn để tổng A + B chia hết cho 45. Tính tích các chữ số của B.
Bài 5. Cho hình bên dưới được tạo bởi 2 hình hộp chữ nhật có chiều dài là 4 cm, chiều rộng là 4 cm và chiều cao là 2 cm. Tính diện tích toàn phần của hình đó.
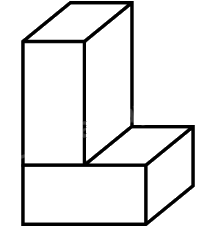
PHẦN 2. TỰ LUẬN
Bài 1. Cho tam giác ABC. Lấy điểm N trên AC sao cho NA = NC x 2 và E trên BC sao cho EC = EB x 3. Nối AE và BN cắt nhau tại I. Biết ${S_{EIB}} = 11$cm2. Hỏi:
a) $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = ?$
b) Tính SABE biết SEIB = 11 cm2
Bài 2. Chú Hải đi Hà Nội từ lúc 8h với vận tốc 35km/h. Đi một lúc thì bị hỏng xe, dừng lại sửa mất 36 phút. Đi tiếp với vận tốc 50km/h thì đến nơi đúng với giờ dự định. Biết quãng đường là 105km.
a) Chú Hải đến nơi lúc mấy giờ?
b) Chú Hải đi với vận tốc 50km/giờ trong bao lâu
c) Lúc 10h, chú Hải đi được bao nhiêu ki-lô-mét?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tổng số tuổi của hai chị em 5 năm trước là 25. Hiện nay tuổi em bằng \(\frac{2}{3}\) tuổi chị. Hỏi năm sau em bao nhiêu tuổi?
Lời giải
Tổng số tuổi hiện nay của hai chị em là:
25 + 5 + 5 = 35 (tuổi)
Ta có sơ đồ:
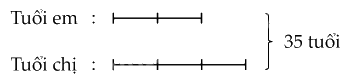
Giá trị một phần là:
35 : (2 + 3) = 7 (tuổi)
Hiện nay tuổi em là:
7 x 2 = 14 (tuổi)
Năm sau, tuổi em là:
14 + 1 = 15 (tuổi)
Đáp số: 15 tuổi
Bài 2. Một đội công nhân có 42 người làm một công việc trong 85 ngày thì xong. Sau 13 ngày thì đội có thêm 12 người nữa. Hỏi đội công nhân chỉ cần thêm bao nhiêu ngày để hoàn thành công việc?
Lời giải
Sau 13 ngày thì 42 người sẽ hoàn thành công việc còn lại sau số ngày là:
85 – 13 = 72 (ngày)
Coi 1 ngày 1 người làm được 1 phần công việc thì số phần công việc còn lại là:
42 x 72 = 3 024 (phần công việc)
Sau khi có thêm 12 người, đội công nhân có số người là:
42 + 12 = 54 (người)
Đội công nhân cần thêm số người để hoàn thành công việc là:
3 024 : 54 = 56 (ngày)
Đáp số: 56 ngày
Bài 3. Nếu có 11 gam khí CO2 thì điều chế được 8 gam khí O2. Nếu có 35,2 gam CO2 thì điều chế được bao nhiêu gam khí O2?
Lời giải
35,2 gam khí CO2 gấp 11 gam khí CO2 số lần là:
35,2 : 11 = 3,2 (lần)
35,3 gam khí CO2 điều chế được số gam khí O2 là:
8 x 3,2 = 25,6 (gam)
Đáp số: 25,6 gam
Bài 4. A là số có 2024 chữ số 9. B là số bé nhất thỏa mãn để tổng A + B chia hết cho 45. Tính tích các chữ số của B.
Lời giải
Để (A + B) chia hết cho 45 thì (A + B) chia hết cho 5 và 9.
A = $\overline {999...99} $ (2024 chữ số 9) chia hết cho 9 nên B phải là số chia hết cho 9.
B có thể là: 0, 9 , 18, 27, 36, ....
Vì A có chữ số tận cùng là 9 nên chia 5 sẽ dư 4 suy ra B chia 5 phải dư 1 thì (A + B) mới chia hết cho 5.
B chia 5 dư 1 thì B có thể là: 1, 6, 11, 16, 21, 26, 31, 36, ....
Để B bé nhất chia hết cho 9 và chia 5 dư 1 thì B = 36.
Tích các chữ số của B là: 3 x 6 = 18.
Đáp số: 18
Bài 5. Cho hình bên dưới được tạo bởi 2 hình hộp chữ nhật có chiều dài là 4 cm, chiều rộng là 4 cm và chiều cao là 2 cm. Tính diện tích toàn phần của hình đó.
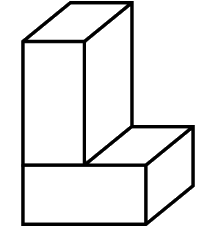
Lời giải
Diện tích toàn phần hình của một hình hộp chữ nhật là:
(4 + 4) x 2 x 2 + 4 x 4 x 2 = 64 (cm2)
Diện tích toàn phần của 2 hình hộp chữ nhật là:
64 x 2 = 128 (cm2)
Vì hình cần tính được tạo bởi 2 hình hộp chữ nhật xếp chồng lên nhau nên diện tích toàn phần hình đó bằng hiệu diện tích toàn phần của 2 hình hộp chữ nhật với 2 lần diện tích mặt tiếp xúc của 2 hình hộp chữ nhật có kích thước 4 cm x 2 cm.
Diện tích toàn phần của hình đó là:
128 – (2 x 4) x 2 = 112 (cm2)
Đáp số: 112 cm2
PHẦN 2. TỰ LUẬN
Bài 1. Cho tam giác ABC. Lấy điểm N trên AC sao cho NA = NC x 2 và E trên BC sao cho EC = EB x 3. Nối AE và BN cắt nhau tại I. Biết ${S_{EIB}} = 11$cm2. Hỏi:
a) $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = ?$
b) Tính SABE biết SEIB = 11 cm2
Lời giải
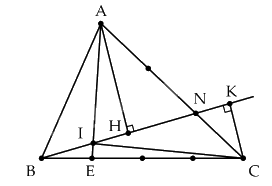
a) Từ A kẻ AH vuông góc với BN và từ C kẻ CK vuông góc với BN.
Ta có $\frac{{{S_{ABN}}}}{{{S_{CBN}}}} = \frac{{AN}}{{NC}} = \frac{2}{1}$ (Chung chiều cao từ đỉnh B)
Mà hai tam giác còn chung đáy BN nên chiều cao AH = $\frac{2}{1}$ chiều cao CK.
Ta có $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = \frac{2}{1}$ vì chung đáy BI, chiều cao AH = $\frac{2}{1}$ chiều cao CK.
b) Ta có $\frac{{{S_{BIE}}}}{{{S_{BIC}}}} = \frac{{BE}}{{BC}} = \frac{1}{4}$ (Chung chiều cao từ I)
Suy ra SBIC = 11 x 4 = 44 (cm2)
Mà $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = \frac{2}{1}$ nên SABI = 44 x 2 = 88 (cm2)
Ta có SBIE + SABI = SABE nên SABE = 88 + 11 = 99 (cm2)
Đáp số: a) $\frac{{{S_{ABI}}}}{{{S_{BIC}}}} = \frac{2}{1}$
b) SABE = 99 cm2
Bài 2. Chú Hải đi Hà Nội từ lúc 8h với vận tốc 35km/h. Đi một lúc thì bị hỏng xe, dừng lại sửa mất 36 phút. Đi tiếp với vận tốc 50km/h thì đến nơi đúng với giờ dự định. Biết quãng đường là 105km.
a) Chú Hải đến nơi lúc mấy giờ?
b) Chú Hải đi với vận tốc 50km/giờ trong bao lâu
c) Lúc 10h, chú Hải đi được bao nhiêu ki-lô-mét?
Lời giải
a) Vì chú Hải đến nơi đúng với giờ dự định, nên thời gian chú Hải đi hết quãng đường là:
105 : 35 = 3 (giờ)
Thời điểm chú Hải đến Hà Nội là:
8 giờ + 3 giờ = 11 (giờ)
b)

Gọi C là điểm mà xe dừng lại nghỉ. Khi đó quãng đường đi còn lại của xe không đổi nên vận tốc tỉ lệ nghịch với thời gian. Tỉ số vận tốc đi trên AC và đi trên BC là: $35:50 = \frac{7}{{10}}$
Tỉ số thời gian đi của xe đi trên AC và đi trên BC là: $\frac{{10}}{7}$
Hiệu thời gian mà xe đi được trên hai quãng đường là: 36 phút = $\frac{3}{5}$ giờ
Thời gian của xe đi với vận tốc 50 km/giờ là:
$\frac{3}{5}:(10 - 7) \times 7 = 1,4$ (giờ) = 1 giờ 24 phút.
c) Thời gian xe đi trên quãng đường AC là:
3 giờ - 36 phút – 1 giờ 24 phút = 1 (giờ)
Thời gian xe đi với vận tốc 50 km/giờ từ C đến lúc 10 giờ là:
10 giờ - 1 giờ - 36 phút = 24 phút = 0,4 (giờ)
Lúc 10 giờ chú Hải đi được số ki – lô- mét là:
35 x 1 + 50 x 0,4 = 55 (km)
Đáp số: a) 11 giờ
b) 1 giờ 24 phút
c) 55 km
Kỳ thi vào lớp 6 trường chuyên Ngoại ngữ là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc làm quen với cấu trúc đề thi và luyện tập thường xuyên là vô cùng cần thiết. Bài viết này sẽ cung cấp thông tin chi tiết về đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2024, cùng với những lời khuyên hữu ích để giúp các em ôn tập hiệu quả.
Đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ thường bao gồm các dạng bài sau:
Tỷ lệ phân bổ điểm giữa các dạng bài có thể thay đổi tùy theo từng năm, nhưng nhìn chung, đề thi thường tập trung vào các chủ đề chính sau:
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2024:
Để đạt kết quả tốt nhất trong kỳ thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ, các em học sinh cần có một kế hoạch ôn tập khoa học và hiệu quả. Dưới đây là một số lời khuyên:
Ngoài sách giáo khoa, các em học sinh có thể tham khảo thêm các tài liệu ôn tập sau:
Trong ngày thi, các em học sinh cần lưu ý những điều sau:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2024!