Giaitoan.edu.vn xin giới thiệu bộ đề thi vào lớp 6 môn Toán trường Thanh Xuân năm 2024 được tổng hợp từ các nguồn uy tín. Đây là tài liệu ôn tập vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các dạng bài tập, từ cơ bản đến nâng cao, kèm theo đáp án chi tiết và lời giải dễ hiểu.
Bốn bạn Việt, Nam, Hòa và Bình cùng góp tiền để mua truyện ủng hộ cho trẻ em vùng cao. Xe thứ nhất đi từ A đến B mất 6 giờ.
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tìm x là số tự nhiên lớn nhất: 15,25 < x < 18,35
A. 15 B. 16 C. 17 D. 18
Bài 2. Điền vào chỗ .......
50cm2 x 8 + 6 dm2 =..........dm2
Bài 3. Phép chia 4,8 : 3,5 có thương là số thập phân có 2 chữ số sau dấu phẩy. Hỏi số dư của phép chia bằng bao nhiêu?
A. 0,005 B. 0,05 C. 0,5 D. 5
Bài 4. Tìm M, biết: M = 0,36 : 0,25 + 36% : 0,5 + 2 x 4 x 0,18
Bài 5. Tổ một của một tốp thợ có 5 người thợ làm việc trong 3 ngày thì làm được 180 m vải. Tổ hai của tốp thợ đó có 7 người thợ và làm việc trong 2 ngày. Hỏi tổ hai của tốp thợ đó làm được bao nhiêu mét vải? (Biết rằng năng suất của mỗi người là như nhau)
Bài 6. Tổng hai số lẻ là 504. Biết giữa hai số có 10 số lẻ khác. Tìm số lẻ bé.
A. 240 B. 241 C. 261 D. 263
Bài 7. Tính diện tích phần tô đậm:
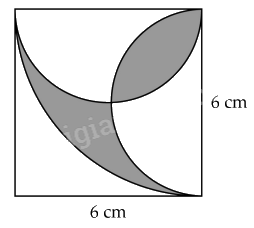
Bài 8. Cùng cộng vào cả tử và mẫu của phân số $\frac{{57}}{{165}}$ một số tự nhiên để bằng phân số $\frac{2}{5}$. Tìm số đó?
Bài 9. Nhân dịp Quốc tế Thiếu Nhi, cửa hàng giảm giá chiếc xe đạp 10% so với giá niêm yết. Tuy nhiên cửa hàng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì cửa hàng lãi bao nhiêu?
A. 8 B. 10 C. 20 D. 22
Bài 10. Biết $AB = \frac{3}{4}CD$, ${S_{AOB}} = 3,6$ cm2. Tính diện tích hình thang ABCD.
Bài 11. Các bao lần lượt là: 40kg; 44kg; 25kg; 60kg; 48kg. Sau khi bán 1 bao gạo nếp thì tổng số gạo tẻ gấp 3 lần tổng số gạo nếp. Hỏi tổng số gạo nếp ban đầu là bao nhiêu?
Bài 12. Trường THCS Thanh Xuân tổ chức đi dã ngoại và có 454 bạn học sinh đi. Nhà trường đã thuê 14 xe. Có 2 loại xe được thuê là loại chở 29 bạn, loại chở 35 bạn. Biết mỗi xe sẽ chở đúng số lượng tiêu chuẩn. Hỏi số xe chở 35 bạn là bao nhiêu xe?
Bài 13. Thả viên sắt hình lập phương cạnh 10 cm vào bể nước thì nước dâng cao ngang cạnh trên của viên sắt, thả viên sắt hình lập phương cạnh 20cm vào bể thì mực nước cao 12 cm. Tính diện tích đáy bể.
Bài 14. Cho dãy: $1\frac{1}{8}\,;\,1\frac{1}{{15}}\,;\,1\frac{1}{{24}}\,;\,1\frac{1}{{35}}\,;...$Tìm số thứ 48.
A. $1\frac{1}{{2448}}$ B. $1\frac{1}{{4848}}$ C. $1\frac{1}{{2499}}$ D. $1\frac{1}{{4899}}$
PHẦN 2. TỰ LUẬN
Bài 15. Bốn bạn Việt, Nam, Hòa và Bình cùng góp tiền để mua truyện ủng hộ cho trẻ em vùng cao. Số tiền Việt góp bằng $\frac{1}{2}$ số tiền 3 bạn còn lại góp. Số tiền Nam góp bằng $\frac{1}{3}$ số tiền mà Việt, Hòa, Bình góp. Số tiền Hòa góp bằng $\frac{1}{4}$ số tiền mà Việt, Nam, Bình góp. Bình góp 130 000 đồng. Hỏi số tiền 4 bạn đã góp là bao nhiêu.
Bài 16. Xe thứ nhất đi từ A đến B mất 6 giờ. Xe thứ hai đi từ A đến B mất 4 giờ. Lúc 6 giờ 15 phút, xe thứ nhất đi từ A đến B. Sau 2 giờ, xe thứ hai đi từ B đến A.
Hỏi hai xe gặp nhau lúc mấy giờ?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tìm x là số tự nhiên lớn nhất: 15,25 < x < 18,35
A. 15 B. 16 C. 17 D. 18
Đáp án: 18
Bài 2. Điền vào chỗ .......
50cm2 x 8 + 6 dm2 =..........dm2
Lời giải
50cm2 x 8 + 6 dm2 = 400 cm2 + 6 dm2 = 4 dm2 + 6 dm2 = 10 dm2
Đáp án: 10
Bài 3. Phép chia 4,8 : 3,5 có thương là số thập phân có 2 chữ số sau dấu phẩy. Hỏi số dư của phép chia bằng bao nhiêu?
A. 0,005 B. 0,05 C. 0,5 D. 5
Bài 4. Tìm M, biết: M = 0,36 : 0,25 + 36% : 0,5 + 2 x 4 x 0,18
Lời giải
M = 0,36 : 0,25 + 36% : 0,5 + 2 x 4 x 0,18
M = $\frac{{36}}{{100}}:\frac{1}{4} + \frac{{36}}{{100}}:\frac{1}{2} + \frac{{36}}{{100}} \times 4$
M = $\frac{{36}}{{100}} \times 4 + \frac{{36}}{{100}} \times 2 + \frac{{36}}{{100}} \times 4$
M = $\frac{{36}}{{100}} \times (4 + 2 + 4)$
M = $\frac{{36}}{{100}} \times 10 = 3,6$
Đáp án: M = 3,6
Bài 5. Tổ một của một tốp thợ có 5 người thợ làm việc trong 3 ngày thì làm được 180 m vải. Tổ hai của tốp thợ đó có 7 người thợ và làm việc trong 2 ngày. Hỏi tổ hai của tốp thợ đó làm được bao nhiêu mét vải? (Biết rằng năng suất của mỗi người là như nhau)
Lời giải
5 người thợ làm trong 1 ngày thì làm được số mét vải là:
180 : 3 = 60 (m)
1 người thợ làm trong 1 ngày thì làm được số mét vải là:
60 : 5 = 12 (m)
7 người thợ làm trong 2 ngày thì làm được số mét vải là:
12 x 7 x 2 = 168 (m)
Đáp án: 168 m vải
Bài 6. Tổng hai số lẻ là 504. Biết giữa hai số có 10 số lẻ khác. Tìm số lẻ bé.
A. 240 B. 241 C. 261 D. 263
Lời giải
Giữa hai số lẻ hơn kém nhau 2 đơn vị. Hiệu của hai số lẻ là: 11 x 2 = 22
Số lẻ bé là: (504 – 22) : 2 = 241
Đáp án: B
Bài 7. Tính diện tích phần tô đậm:
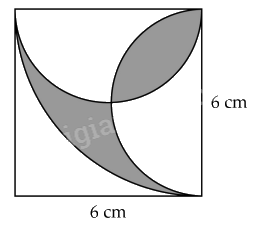
Lời giải
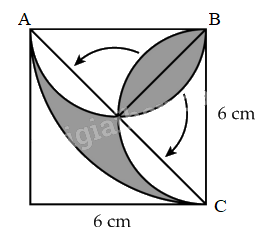
Diện tích tô đậm bằng hiệu của $\frac{1}{4}$ diện tích hình tròn tâm B bán kính 6 cm với diện tích hình tam giác vuông ABC.
$\frac{1}{4}$ diện tích hình tròn tâm B bán kính 6 cm là: 6 x 6 x 3,14 x $\frac{1}{4}$ = 28,26 (cm2)
Diện tích hình tam giác vuông ABC là: 6 6 : 2 = 18 (cm2)
Diện tích tô đậm là: 28,26 – 18 = 10,26 (cm2)
Đáp án: 10,26 cm2
Bài 8. Cùng cộng vào cả tử và mẫu của phân số $\frac{{57}}{{165}}$ một số tự nhiên để bằng phân số $\frac{2}{5}$. Tìm số đó?
Lời giải
Cộng vào tử số và mẫu số cùng một đơn vị thì hiệu của mẫu số và tử số không thay đổi.
Hiệu của mẫu số và tử số ban đầu là: 165 – 57 = 108
Ta có sơ đồ:

Tử số mới là: 108 : (5 – 2) x 2 = 72
Số cần thêm là: 72 – 57 = 15
Đáp án: 15
Bài 9. Nhân dịp Quốc tế Thiếu Nhi, cửa hàng giảm giá chiếc xe đạp 10% so với giá niêm yết. Tuy nhiên cửa hàng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì cửa hàng lãi bao nhiêu?
A. 8 B. 10 C. 20 D. 22
Lời giải
Giá bán mới so với giá niêm yết là: 100% - 10% = 90% (giá niêm yết)
Giá bán mới so với giá vốn là: 100% + 8% = 108% (giá vốn)
Giá niêm yết so với giá vốn là: 108% : 90% = 120% (giá vốn)
Nếu không giảm giá thì cửa hàng lãi số phần trăm là: 120% - 100% = 20%
Đáp án: C
Bài 10. Biết $AB = \frac{3}{4}CD$, ${S_{AOB}} = 3,6$ cm2. Tính diện tích hình thang ABCD.
Lời giải
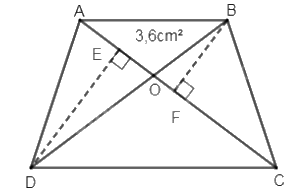
$\frac{{{S_{ABC}}}}{{{S_{ADC}}}} = \frac{{AB}}{{CD}} = \frac{3}{4}$ (chiều cao đều bằng chiều cao của hình thang, đáy $AB = \frac{3}{4}CD$)
Nếu coi AC là đáy chung thì chiều cao $BF = \frac{3}{4}DE$
Suy ra ${S_{AOB}} = \frac{3}{4}{S_{AOD}}$ (có chung đáy AO, chiều cao $BF = \frac{3}{4}DE$)
Diện tích tam giác AOD là $3,6:\frac{3}{4} = 4,8$ cm2
${S_{ABD}} = {S_{DAO}} + {S_{AOB}} = 4,8 + 3,6 = 8,4$ (cm2)
${S_{ABD}} = \frac{3}{4}{S_{BDC}}$ (có đáy $AB = \frac{3}{4}CD$ và chiều cao đều bằng chiều cao của hình thang)
${S_{BDC}} = 8,4 \times \frac{4}{3} = 11,2$ (cm2)
Vậy diện tích hình thang ABCD là: 8,4 + 11,2 = 19,6 (cm2)
Đáp án: 19,6 cm2
Bài 11. Các bao lần lượt là: 40kg; 44kg; 25kg; 60kg; 48kg. Sau khi bán 1 bao gạo nếp thì tổng số gạo tẻ gấp 3 lần tổng số gạo nếp. Hỏi tổng số gạo nếp ban đầu là bao nhiêu?
Lời giải
Tổng khối lượng 5 bao gạo là: 40 + 44 + 25 + 60 + 48 = 217 (kg)
Sau khi bán 1 bao gạo nếp thì tổng số bao gạo tẻ gấp 3 lần tổng số bao gạo nếp
Suy ra số tổng khối lượng của bốn bao còn lại chia hết cho 4.
Ta có: 217 : 4 dư 1 nên số bao gạo nếp bị bán đi chia 4 dư 1. Suy ra số bao gạo nếp bị bán đi là 25 kg.
Số ki-lô-gam gạo nếp còn lại là: (217 – 25) : (1 + 3) x 1 = 48 (kg)
Tổng số gạo nếp ban đầu là: 48 + 25 = 73 (kg)
Đáp án: 73 kg
Bài 12. Trường THCS Thanh Xuân tổ chức đi dã ngoại và có 454 bạn học sinh đi. Nhà trường đã thuê 14 xe. Có 2 loại xe được thuê là loại chở 29 bạn, loại chở 35 bạn. Biết mỗi xe sẽ chở đúng số lượng tiêu chuẩn. Hỏi số xe chở 35 bạn là bao nhiêu xe?
Lời giải
Giả sử tất cả đều là xe chở 29 bạn thì 14 xe chở được số học sinh là:
29 x 14 = 406 (học sinh)
Số học sinh chưa được lên xe là:
454 – 406 = 48 (học sinh)
Có số xe loại chở 35 bạn là:
48 : (35 – 29) = 8 (xe)
Đáp án: 8 xe
Bài 13. Thả viên sắt hình lập phương cạnh 10 cm vào bể nước thì nước dâng cao ngang cạnh trên của viên sắt, thả viên sắt hình lập phương cạnh 20cm vào bể thì mực nước cao 12 cm. Tính diện tích đáy bể.
Lời giải
Thả viên sắt hình lập phương cạnh 10 cm vào bể nước thì phần nước dâng lên có dạng là đáy của bể với chiều cao bằng 10 cm.
Thể tích của hình lập phương cạnh 10 cm là:
10 x 10 x 10 = 1 000 (cm3)
Thả viên sắt hình lập phương cạnh 20 cm thì phần nước dâng lên có dạng là đáy của bể với chiều cao là 12 cm.
Thể tích tích của phần viên sắt chìm trong nước là:
20 x 20 x 20 = 4 800 (cm3)
Cùng một diện tích đáy bể thì thể tích chêch lệch chính là bằng thể tích phần nước dâng cao hơn.
Thể tích viên sắt cạnh 20 cm chiếm nhiều hơn thể thích viên sắt cạnh 10 cm chiếm là:
4 800 – 1 000 = 3 800 (cm3)
Thể tích này ứng với thể tích nước dâng lên cao hơn: 12 - 10 = 2 (cm)
Diện tích đáy bể là:
3 800 : 2 = 1 900 (cm2)
Đáp án: 1 900 cm2
Bài 14. Cho dãy: $1\frac{1}{8}\,;\,1\frac{1}{{15}}\,;\,1\frac{1}{{24}}\,;\,1\frac{1}{{35}}\,;...$Tìm số thứ 48.
A. $1\frac{1}{{2448}}$ B. $1\frac{1}{{4848}}$ C. $1\frac{1}{{2499}}$ D. $1\frac{1}{{4899}}$
Lời giải
$1\frac{1}{8} = \frac{9}{8} = \frac{{3 \times 3}}{{2 \times 4}}$
$1\frac{1}{{15}} = \frac{{16}}{{15}} = \frac{{4 \times 4}}{{3 \times 5}}$
$1\frac{1}{{24}} = \frac{{25}}{{24}} = \frac{{5 \times 5}}{{4 \times 6}}$
Vậy số thứ 48 là $\frac{{50 \times 50}}{{49 \times 51}} = \frac{{2500}}{{2499}} = 1\frac{1}{{2499}}$
PHẦN 2. TỰ LUẬN
Bài 15. Bốn bạn Việt, Nam, Hòa và Bình cùng góp tiền để mua truyện ủng hộ cho trẻ em vùng cao. Số tiền Việt góp bằng $\frac{1}{2}$ số tiền 3 bạn còn lại góp. Số tiền Nam góp bằng $\frac{1}{3}$ số tiền mà Việt, Hòa, Bình góp. Số tiền Hòa góp bằng $\frac{1}{4}$ số tiền mà Việt, Nam, Bình góp. Bình góp 130 000 đồng. Hỏi số tiền 4 bạn đã góp là bao nhiêu.
Lời giải
Số tiền bạn Việt góp so với số tiền cả bốn bạn là: $\frac{1}{{2 + 1}} = \frac{1}{3}$
Số tiền bạn Nam góp so với số tiền cả bốn bạn là: $\frac{1}{{3 + 1}} = \frac{1}{4}$
Số tiền bạn Hòa góp so với số tiền cả bốn bạn là: $\frac{1}{{4 + 1}} = \frac{1}{5}$
Số tiền Bình góp so với số tiền cả bốn bạn là: $1 - \left( {\frac{1}{3} + \frac{1}{4} + \frac{1}{5}} \right) = \frac{{13}}{{60}}$
Số tiền bốn bạn đã góp là: $130000:\frac{{13}}{{60}} = 600000$ (đồng)
Đáp số: 600 000 đồng
Bài 16. Xe thứ nhất đi từ A đến B mất 6 giờ. Xe thứ hai đi từ A đến B mất 4 giờ. Lúc 6 giờ 15 phút, xe thứ nhất đi từ A đến B. Sau 2 giờ, xe thứ hai đi từ B đến A.
Hỏi hai xe gặp nhau lúc mấy giờ?
Lời giải
Mỗi giờ xe thứ nhất đi được: $1:6 = \frac{1}{6}$ (quãng đường)
Mỗi giờ xe thứ hai đi được: $1:4 = \frac{1}{4}$ (quãng đường)
Sau 2 giờ, xe thứ nhất đã đi được số phần quãng đường là: $2:6 = \frac{1}{3}$ (quãng đường)
Hai xe cùng đi tiếp số phần quãng đường là: $1 - \frac{1}{3} = \frac{2}{3}$ (quãng đường)
Thời gian để hai xe gặp nhau là: $\frac{2}{3}:\left( {\frac{1}{6} + \frac{1}{4}} \right) = \frac{8}{5}$ (giờ) = 1 giờ 36 phút
Hai xe gặp nhau vào thời điểm là:
6 giờ 15 phút + 2 giờ + 1 giờ 36 phút = 9 giờ 51 phút
Đáp số: 9 giờ 51 phút
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tìm x là số tự nhiên lớn nhất: 15,25 < x < 18,35
A. 15 B. 16 C. 17 D. 18
Bài 2. Điền vào chỗ .......
50cm2 x 8 + 6 dm2 =..........dm2
Bài 3. Phép chia 4,8 : 3,5 có thương là số thập phân có 2 chữ số sau dấu phẩy. Hỏi số dư của phép chia bằng bao nhiêu?
A. 0,005 B. 0,05 C. 0,5 D. 5
Bài 4. Tìm M, biết: M = 0,36 : 0,25 + 36% : 0,5 + 2 x 4 x 0,18
Bài 5. Tổ một của một tốp thợ có 5 người thợ làm việc trong 3 ngày thì làm được 180 m vải. Tổ hai của tốp thợ đó có 7 người thợ và làm việc trong 2 ngày. Hỏi tổ hai của tốp thợ đó làm được bao nhiêu mét vải? (Biết rằng năng suất của mỗi người là như nhau)
Bài 6. Tổng hai số lẻ là 504. Biết giữa hai số có 10 số lẻ khác. Tìm số lẻ bé.
A. 240 B. 241 C. 261 D. 263
Bài 7. Tính diện tích phần tô đậm:
Bài 8. Cùng cộng vào cả tử và mẫu của phân số $\frac{{57}}{{165}}$ một số tự nhiên để bằng phân số $\frac{2}{5}$. Tìm số đó?
Bài 9. Nhân dịp Quốc tế Thiếu Nhi, cửa hàng giảm giá chiếc xe đạp 10% so với giá niêm yết. Tuy nhiên cửa hàng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì cửa hàng lãi bao nhiêu?
A. 8 B. 10 C. 20 D. 22
Bài 10. Biết $AB = \frac{3}{4}CD$, ${S_{AOB}} = 3,6$ cm2. Tính diện tích hình thang ABCD.
Bài 11. Các bao lần lượt là: 40kg; 44kg; 25kg; 60kg; 48kg. Sau khi bán 1 bao gạo nếp thì tổng số gạo tẻ gấp 3 lần tổng số gạo nếp. Hỏi tổng số gạo nếp ban đầu là bao nhiêu?
Bài 12. Trường THCS Thanh Xuân tổ chức đi dã ngoại và có 454 bạn học sinh đi. Nhà trường đã thuê 14 xe. Có 2 loại xe được thuê là loại chở 29 bạn, loại chở 35 bạn. Biết mỗi xe sẽ chở đúng số lượng tiêu chuẩn. Hỏi số xe chở 35 bạn là bao nhiêu xe?
Bài 13. Thả viên sắt hình lập phương cạnh 10 cm vào bể nước thì nước dâng cao ngang cạnh trên của viên sắt, thả viên sắt hình lập phương cạnh 20cm vào bể thì mực nước cao 12 cm. Tính diện tích đáy bể.
Bài 14. Cho dãy: $1\frac{1}{8}\,;\,1\frac{1}{{15}}\,;\,1\frac{1}{{24}}\,;\,1\frac{1}{{35}}\,;...$Tìm số thứ 48.
A. $1\frac{1}{{2448}}$ B. $1\frac{1}{{4848}}$ C. $1\frac{1}{{2499}}$ D. $1\frac{1}{{4899}}$
PHẦN 2. TỰ LUẬN
Bài 15. Bốn bạn Việt, Nam, Hòa và Bình cùng góp tiền để mua truyện ủng hộ cho trẻ em vùng cao. Số tiền Việt góp bằng $\frac{1}{2}$ số tiền 3 bạn còn lại góp. Số tiền Nam góp bằng $\frac{1}{3}$ số tiền mà Việt, Hòa, Bình góp. Số tiền Hòa góp bằng $\frac{1}{4}$ số tiền mà Việt, Nam, Bình góp. Bình góp 130 000 đồng. Hỏi số tiền 4 bạn đã góp là bao nhiêu.
Bài 16. Xe thứ nhất đi từ A đến B mất 6 giờ. Xe thứ hai đi từ A đến B mất 4 giờ. Lúc 6 giờ 15 phút, xe thứ nhất đi từ A đến B. Sau 2 giờ, xe thứ hai đi từ B đến A.
Hỏi hai xe gặp nhau lúc mấy giờ?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Bài 1. Tìm x là số tự nhiên lớn nhất: 15,25 < x < 18,35
A. 15 B. 16 C. 17 D. 18
Đáp án: 18
Bài 2. Điền vào chỗ .......
50cm2 x 8 + 6 dm2 =..........dm2
Lời giải
50cm2 x 8 + 6 dm2 = 400 cm2 + 6 dm2 = 4 dm2 + 6 dm2 = 10 dm2
Đáp án: 10
Bài 3. Phép chia 4,8 : 3,5 có thương là số thập phân có 2 chữ số sau dấu phẩy. Hỏi số dư của phép chia bằng bao nhiêu?
A. 0,005 B. 0,05 C. 0,5 D. 5
Bài 4. Tìm M, biết: M = 0,36 : 0,25 + 36% : 0,5 + 2 x 4 x 0,18
Lời giải
M = 0,36 : 0,25 + 36% : 0,5 + 2 x 4 x 0,18
M = $\frac{{36}}{{100}}:\frac{1}{4} + \frac{{36}}{{100}}:\frac{1}{2} + \frac{{36}}{{100}} \times 4$
M = $\frac{{36}}{{100}} \times 4 + \frac{{36}}{{100}} \times 2 + \frac{{36}}{{100}} \times 4$
M = $\frac{{36}}{{100}} \times (4 + 2 + 4)$
M = $\frac{{36}}{{100}} \times 10 = 3,6$
Đáp án: M = 3,6
Bài 5. Tổ một của một tốp thợ có 5 người thợ làm việc trong 3 ngày thì làm được 180 m vải. Tổ hai của tốp thợ đó có 7 người thợ và làm việc trong 2 ngày. Hỏi tổ hai của tốp thợ đó làm được bao nhiêu mét vải? (Biết rằng năng suất của mỗi người là như nhau)
Lời giải
5 người thợ làm trong 1 ngày thì làm được số mét vải là:
180 : 3 = 60 (m)
1 người thợ làm trong 1 ngày thì làm được số mét vải là:
60 : 5 = 12 (m)
7 người thợ làm trong 2 ngày thì làm được số mét vải là:
12 x 7 x 2 = 168 (m)
Đáp án: 168 m vải
Bài 6. Tổng hai số lẻ là 504. Biết giữa hai số có 10 số lẻ khác. Tìm số lẻ bé.
A. 240 B. 241 C. 261 D. 263
Lời giải
Giữa hai số lẻ hơn kém nhau 2 đơn vị. Hiệu của hai số lẻ là: 11 x 2 = 22
Số lẻ bé là: (504 – 22) : 2 = 241
Đáp án: B
Bài 7. Tính diện tích phần tô đậm:
Lời giải
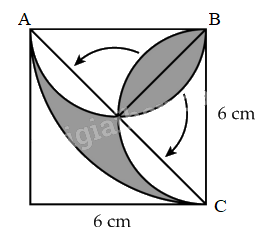
Diện tích tô đậm bằng hiệu của $\frac{1}{4}$ diện tích hình tròn tâm B bán kính 6 cm với diện tích hình tam giác vuông ABC.
$\frac{1}{4}$ diện tích hình tròn tâm B bán kính 6 cm là: 6 x 6 x 3,14 x $\frac{1}{4}$ = 28,26 (cm2)
Diện tích hình tam giác vuông ABC là: 6 6 : 2 = 18 (cm2)
Diện tích tô đậm là: 28,26 – 18 = 10,26 (cm2)
Đáp án: 10,26 cm2
Bài 8. Cùng cộng vào cả tử và mẫu của phân số $\frac{{57}}{{165}}$ một số tự nhiên để bằng phân số $\frac{2}{5}$. Tìm số đó?
Lời giải
Cộng vào tử số và mẫu số cùng một đơn vị thì hiệu của mẫu số và tử số không thay đổi.
Hiệu của mẫu số và tử số ban đầu là: 165 – 57 = 108
Ta có sơ đồ:

Tử số mới là: 108 : (5 – 2) x 2 = 72
Số cần thêm là: 72 – 57 = 15
Đáp án: 15
Bài 9. Nhân dịp Quốc tế Thiếu Nhi, cửa hàng giảm giá chiếc xe đạp 10% so với giá niêm yết. Tuy nhiên cửa hàng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì cửa hàng lãi bao nhiêu?
A. 8 B. 10 C. 20 D. 22
Lời giải
Giá bán mới so với giá niêm yết là: 100% - 10% = 90% (giá niêm yết)
Giá bán mới so với giá vốn là: 100% + 8% = 108% (giá vốn)
Giá niêm yết so với giá vốn là: 108% : 90% = 120% (giá vốn)
Nếu không giảm giá thì cửa hàng lãi số phần trăm là: 120% - 100% = 20%
Đáp án: C
Bài 10. Biết $AB = \frac{3}{4}CD$, ${S_{AOB}} = 3,6$ cm2. Tính diện tích hình thang ABCD.
Lời giải
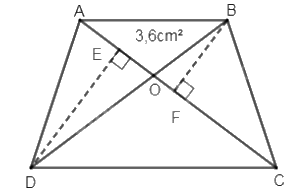
$\frac{{{S_{ABC}}}}{{{S_{ADC}}}} = \frac{{AB}}{{CD}} = \frac{3}{4}$ (chiều cao đều bằng chiều cao của hình thang, đáy $AB = \frac{3}{4}CD$)
Nếu coi AC là đáy chung thì chiều cao $BF = \frac{3}{4}DE$
Suy ra ${S_{AOB}} = \frac{3}{4}{S_{AOD}}$ (có chung đáy AO, chiều cao $BF = \frac{3}{4}DE$)
Diện tích tam giác AOD là $3,6:\frac{3}{4} = 4,8$ cm2
${S_{ABD}} = {S_{DAO}} + {S_{AOB}} = 4,8 + 3,6 = 8,4$ (cm2)
${S_{ABD}} = \frac{3}{4}{S_{BDC}}$ (có đáy $AB = \frac{3}{4}CD$ và chiều cao đều bằng chiều cao của hình thang)
${S_{BDC}} = 8,4 \times \frac{4}{3} = 11,2$ (cm2)
Vậy diện tích hình thang ABCD là: 8,4 + 11,2 = 19,6 (cm2)
Đáp án: 19,6 cm2
Bài 11. Các bao lần lượt là: 40kg; 44kg; 25kg; 60kg; 48kg. Sau khi bán 1 bao gạo nếp thì tổng số gạo tẻ gấp 3 lần tổng số gạo nếp. Hỏi tổng số gạo nếp ban đầu là bao nhiêu?
Lời giải
Tổng khối lượng 5 bao gạo là: 40 + 44 + 25 + 60 + 48 = 217 (kg)
Sau khi bán 1 bao gạo nếp thì tổng số bao gạo tẻ gấp 3 lần tổng số bao gạo nếp
Suy ra số tổng khối lượng của bốn bao còn lại chia hết cho 4.
Ta có: 217 : 4 dư 1 nên số bao gạo nếp bị bán đi chia 4 dư 1. Suy ra số bao gạo nếp bị bán đi là 25 kg.
Số ki-lô-gam gạo nếp còn lại là: (217 – 25) : (1 + 3) x 1 = 48 (kg)
Tổng số gạo nếp ban đầu là: 48 + 25 = 73 (kg)
Đáp án: 73 kg
Bài 12. Trường THCS Thanh Xuân tổ chức đi dã ngoại và có 454 bạn học sinh đi. Nhà trường đã thuê 14 xe. Có 2 loại xe được thuê là loại chở 29 bạn, loại chở 35 bạn. Biết mỗi xe sẽ chở đúng số lượng tiêu chuẩn. Hỏi số xe chở 35 bạn là bao nhiêu xe?
Lời giải
Giả sử tất cả đều là xe chở 29 bạn thì 14 xe chở được số học sinh là:
29 x 14 = 406 (học sinh)
Số học sinh chưa được lên xe là:
454 – 406 = 48 (học sinh)
Có số xe loại chở 35 bạn là:
48 : (35 – 29) = 8 (xe)
Đáp án: 8 xe
Bài 13. Thả viên sắt hình lập phương cạnh 10 cm vào bể nước thì nước dâng cao ngang cạnh trên của viên sắt, thả viên sắt hình lập phương cạnh 20cm vào bể thì mực nước cao 12 cm. Tính diện tích đáy bể.
Lời giải
Thả viên sắt hình lập phương cạnh 10 cm vào bể nước thì phần nước dâng lên có dạng là đáy của bể với chiều cao bằng 10 cm.
Thể tích của hình lập phương cạnh 10 cm là:
10 x 10 x 10 = 1 000 (cm3)
Thả viên sắt hình lập phương cạnh 20 cm thì phần nước dâng lên có dạng là đáy của bể với chiều cao là 12 cm.
Thể tích tích của phần viên sắt chìm trong nước là:
20 x 20 x 20 = 4 800 (cm3)
Cùng một diện tích đáy bể thì thể tích chêch lệch chính là bằng thể tích phần nước dâng cao hơn.
Thể tích viên sắt cạnh 20 cm chiếm nhiều hơn thể thích viên sắt cạnh 10 cm chiếm là:
4 800 – 1 000 = 3 800 (cm3)
Thể tích này ứng với thể tích nước dâng lên cao hơn: 12 - 10 = 2 (cm)
Diện tích đáy bể là:
3 800 : 2 = 1 900 (cm2)
Đáp án: 1 900 cm2
Bài 14. Cho dãy: $1\frac{1}{8}\,;\,1\frac{1}{{15}}\,;\,1\frac{1}{{24}}\,;\,1\frac{1}{{35}}\,;...$Tìm số thứ 48.
A. $1\frac{1}{{2448}}$ B. $1\frac{1}{{4848}}$ C. $1\frac{1}{{2499}}$ D. $1\frac{1}{{4899}}$
Lời giải
$1\frac{1}{8} = \frac{9}{8} = \frac{{3 \times 3}}{{2 \times 4}}$
$1\frac{1}{{15}} = \frac{{16}}{{15}} = \frac{{4 \times 4}}{{3 \times 5}}$
$1\frac{1}{{24}} = \frac{{25}}{{24}} = \frac{{5 \times 5}}{{4 \times 6}}$
Vậy số thứ 48 là $\frac{{50 \times 50}}{{49 \times 51}} = \frac{{2500}}{{2499}} = 1\frac{1}{{2499}}$
PHẦN 2. TỰ LUẬN
Bài 15. Bốn bạn Việt, Nam, Hòa và Bình cùng góp tiền để mua truyện ủng hộ cho trẻ em vùng cao. Số tiền Việt góp bằng $\frac{1}{2}$ số tiền 3 bạn còn lại góp. Số tiền Nam góp bằng $\frac{1}{3}$ số tiền mà Việt, Hòa, Bình góp. Số tiền Hòa góp bằng $\frac{1}{4}$ số tiền mà Việt, Nam, Bình góp. Bình góp 130 000 đồng. Hỏi số tiền 4 bạn đã góp là bao nhiêu.
Lời giải
Số tiền bạn Việt góp so với số tiền cả bốn bạn là: $\frac{1}{{2 + 1}} = \frac{1}{3}$
Số tiền bạn Nam góp so với số tiền cả bốn bạn là: $\frac{1}{{3 + 1}} = \frac{1}{4}$
Số tiền bạn Hòa góp so với số tiền cả bốn bạn là: $\frac{1}{{4 + 1}} = \frac{1}{5}$
Số tiền Bình góp so với số tiền cả bốn bạn là: $1 - \left( {\frac{1}{3} + \frac{1}{4} + \frac{1}{5}} \right) = \frac{{13}}{{60}}$
Số tiền bốn bạn đã góp là: $130000:\frac{{13}}{{60}} = 600000$ (đồng)
Đáp số: 600 000 đồng
Bài 16. Xe thứ nhất đi từ A đến B mất 6 giờ. Xe thứ hai đi từ A đến B mất 4 giờ. Lúc 6 giờ 15 phút, xe thứ nhất đi từ A đến B. Sau 2 giờ, xe thứ hai đi từ B đến A.
Hỏi hai xe gặp nhau lúc mấy giờ?
Lời giải
Mỗi giờ xe thứ nhất đi được: $1:6 = \frac{1}{6}$ (quãng đường)
Mỗi giờ xe thứ hai đi được: $1:4 = \frac{1}{4}$ (quãng đường)
Sau 2 giờ, xe thứ nhất đã đi được số phần quãng đường là: $2:6 = \frac{1}{3}$ (quãng đường)
Hai xe cùng đi tiếp số phần quãng đường là: $1 - \frac{1}{3} = \frac{2}{3}$ (quãng đường)
Thời gian để hai xe gặp nhau là: $\frac{2}{3}:\left( {\frac{1}{6} + \frac{1}{4}} \right) = \frac{8}{5}$ (giờ) = 1 giờ 36 phút
Hai xe gặp nhau vào thời điểm là:
6 giờ 15 phút + 2 giờ + 1 giờ 36 phút = 9 giờ 51 phút
Đáp số: 9 giờ 51 phút
Kỳ thi vào lớp 6 môn Toán trường Thanh Xuân là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các kiến thức Toán học đã học ở bậc Tiểu học, tập trung vào các chủ đề chính như:
Dựa trên các đề thi chính thức của trường Thanh Xuân trong những năm trước, cấu trúc đề thi vào lớp 6 môn Toán thường bao gồm:
Để đạt kết quả tốt nhất trong kỳ thi vào lớp 6 môn Toán trường Thanh Xuân, các em học sinh cần có một kế hoạch ôn tập khoa học và hiệu quả. Dưới đây là một số gợi ý:
Luyện đề là một bước không thể thiếu trong quá trình ôn thi vào lớp 6 môn Toán. Việc luyện đề giúp các em học sinh:
Giaitoan.edu.vn tự hào là một trong những website hàng đầu cung cấp tài liệu ôn thi vào lớp 6 môn Toán chất lượng cao. Chúng tôi cam kết mang đến cho các em học sinh những bộ đề thi mới nhất, đáp án chi tiết và lời giải dễ hiểu. Hãy truy cập giaitoan.edu.vn ngay hôm nay để bắt đầu hành trình chinh phục kỳ thi vào lớp 6 môn Toán trường Thanh Xuân năm 2024!
Bài toán: Một khu vườn hình chữ nhật có chiều dài 15m, chiều rộng 8m. Tính diện tích khu vườn đó.
Giải:
Diện tích khu vườn hình chữ nhật là:
15m x 8m = 120m2
Đáp số: 120m2
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi vào lớp 6 môn Toán trường Thanh Xuân năm 2024!