Giaitoan.edu.vn xin giới thiệu bộ đề thi vào lớp 6 môn Toán trường Cầu Giấy năm 2022 chính thức, được tổng hợp đầy đủ và cập nhật liên tục. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi tuyển sinh.
Chúng tôi cung cấp không chỉ đề thi mà còn cả đáp án chi tiết và phương pháp giải bài tập, giúp các em hiểu rõ bản chất của từng dạng toán.
Một hình hộp hình chữ nhật có chiều dài là 12 cm, chiều rộng là 8 cm... Tổng số học sinh khối 5 của một trường tiểu học là một số có ba chữ số ...
ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS CẦU GIẤY
NĂM HỌC 2022 – 2023
Thời gian làm bài: 45 phút
Phần 1: Trắc nghiệm(Mỗi câu hỏi 0,75 điểm)
Câu 1. Tính: $3,5 \times \frac{1}{4} - 1,5 \times \frac{1}{4}$
A. 0
B. $\frac{1}{2}$
C. $\frac{5}{4}$
D. $\frac{1}{8}$
Câu 2. 0,2 m3 gấp 25 dm3 số lần là
A. 0,008
B. 0,8
C. 8
D. 80
Câu 3. Một ô tô đi với vận tốc 60 km/giờ, tính quãng đường ô tô đi được trong 12 phút.
A. 0,2 km
B. 5 km
C. 720 km
D. 12 km
Câu 4. Một hình hộp hình chữ nhật có chiều dài là 12 cm, chiều rộng là 8 cm. Một hình lập phương có cạnh bằng trung bình cộng ba kích thước của hình hộp chữ nhật và có diện tích toàn phần là 486 cm2. Tìm chiều cao của hình hộp chữ nhật.
A. 7 cm
B. 8 cm
C. 9 cm
D. 81 cm
Phần 2: Điền đáp số (Mỗi câu 1 điềm)
Câu 5. Tìm $x$, biết: $15,25 - 5 \times x = 0,75$
Trả lời: ......................
Câu 6. Tổng số học sinh khối 5 của một trường tiểu học là một số có ba chữ số và chữ số hàng trăm là 2. Biết khi xếp học sinh thành 10 hàng thì dư 5 học sinh và xếp thành 9 hàng thì không dư. Hỏi số học sinh khối 5 là bao nhiêu?
Trả lời: .................
Câu 7. Tuổi anh bằng $\frac{5}{4}$ tuổi em. Biết hai lần tuổi anh cộng với tuổi em là 28 tuổi. Tính số tuổi của anh.
Trả lời: ......................
Câu 8. Cho hình thang ABCD có hai đáy AB, CD. Hai đường chéo AC và BD cắt nhau tại O. Biết diện tích tam giác OAD là 11 cm2, diện tích tam giác OAB là 5 cm2. Tính diện tích hình thang ABCD.
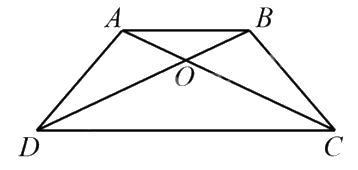
Trả lời: .......................
Phần 3: Tự luận
Bài 1 (2 điểm). Một cuộc thi vẽ có 120 học sinh đạt giải. Số học sinh đạt giải nhất bằng 10% tổng số học sinh đạt giải, số học sinh đạt giải nhì bằng $\frac{1}{5}$ tổng số học sinh đạt ba giải còn lại, số học sinh đạt giải ba bằng $\frac{3}{5}$ số học sinh đạt giải khuyến khích.
a) Tính số học sinh đạt giải nhất.
b) Tính số học sinh đạt giải khuyến khích
Bài 2 (1 điểm). Trong kì thi chọn HSG có 2 môn thi là Toán và Tiếng Anh. Biết $\frac{1}{{10}}$ số học sinh giỏi Tiếng Anh bằng $\frac{6}{{83}}$ số học sinh giỏi Toán. Số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là một số có hai chữ số, chia cho 5 và 9 đều dư 2. Tính số học sinh giỏi Toán, số học sinh giỏi Tiếng Anh.
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1. Trắc nghiệm
Câu 1
$3,5 \times \frac{1}{4} - 1,5 \times \frac{1}{4} = (3,5 - 1,5) \times \frac{1}{4} = 2 \times \frac{1}{4} = \frac{1}{2}$
Chọn B
Câu 2
Đổi 0,2 m3 = 200 dm3
0,2 m3 gấp 25 dm3 số lần là 200 : 25 = 8 (lần)
Chọn C
Câu 3
Đổi 12 phút = $\frac{1}{5}$ giờ
Quãng đường ô tô đi được trong 12 phút là $60 \times \frac{1}{5} = 12$ (km)
Chọn D
Câu 4
Diện tích một mặt của hình lập phương là 486 : 6 = 81 (cm2)
Vì 81 = 9 x 9 nên cạnh hình lập phương có độ dài là 9 cm
Tổng độ dài 3 kích thước của hình hộp chữ nhật là 9 x 3 = 27 (cm)
Chiều cao của hình hộp chữ nhật là 27 – 12 – 8 = 7 (cm)
Chọn A
Phần 2. Điền đáp số
Câu 5
$15,25 - 5 \times x = 0,75$
$5 \times x = 15,25 - 0,75$
$5 \times x = 14,5$
$x = 14,5:5$
$x = 2,9$
Câu 6
Gọi số học sinh của khối 5 là $\overline {2ab} $
Vì khi xếp học sinh thành 10 hàng thì dư 5 học sinh nên số học sinh là số chia 10 dư 5
Suy ra b = 5
Vì số học sinh xếp thành 9 hàng thì không dư nên $\overline {2a5} $ chia hết cho 9.
Suy ra (2 + a + 5) chia hết cho 9 nên a = 2
Vậy khối 5 có 225 học sinh.
Câu 7
Coi tuổi anh là 5 phần thì tuổi em là 4 phần.
Khi đó, 2 lần tuổi anh là 10 phần.
28 tuổi ứng với: 10 + 4 = 14 (phần)
Tuổi anh là 28 : 14 x 5 = 10 (tuổi)
Đáp số: 10 tuổi
Câu 8
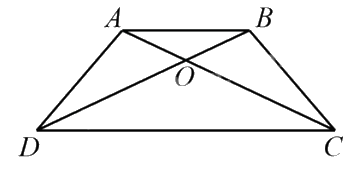
${S_{CAB}} = {S_{DAB}}$ (Chung đáy AB và chiều cao bằng nhau)
Mà ${S_{DAB}} = {S_{OAB}} + {S_{OAD}} = 5 + 11 = 16$ (cm2) nên ${S_{CAB}} = 16$ cm2
$ \Rightarrow {S_{OBC}} = {S_{CAB}} - {S_{OAB}} = 16 - 5 = 11$ (cm2)
Ta có $\frac{{{S_{AOB}}}}{{{S_{AOD}}}} = \frac{{OB}}{{OD}} = \frac{5}{{11}}$ (Hai tam giác có chung chiều cao hạ từ A xuống BD)
Ta có $\frac{{{S_{OBC}}}}{{{S_{ODC}}}} = \frac{{OB}}{{OD}}$ (Hai tam giác có chung chiều cao hạ từ C xuống đáy BD)
Suy ra $\frac{{11}}{{{S_{ODC}}}} = \frac{5}{{11}}$ $ \Rightarrow $ SODC = 11 x 11 : 5 = 24,2 (cm2)
SABCD = SABD + SOBC + SODC = 16 + 11 + 24,2 = 51,2 (cm2)
Đáp số: 51,2 cm2
Phần 3: Tự luận
Bài 1
a) Số học sinh đạt giải nhất
120 x 10 : 100 = 12 (học sinh)
b) Vì số học sinh đạt giải nhì bằng $\frac{1}{5}$ tổng số học sinh đạt ba giải còn lại nên số học sinh đạt giải nhì bằng $\frac{1}{6}$ tổng số học sinh đạt giải.
Số học sinh đạt giải nhì là
$120 \times \frac{1}{6} = 20$ (học sinh)
Tổng số học sinh đạt giải ba và giải khuyến khích là
120 – 12 – 20 = 88 (học sinh)
Số học sinh đạt giải khuyến khích là
88 : (3 + 5) x 5 = 55 (học sinh)
Đáp số: a) 12 học sinh;
b) 55 học sinh
Bài 2
Các số có hai chữ số chia cho 5 và 9 đều dư 2 là 47 và 92.
Do đó số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là 47 bạn và 92 bạn.
Biết $\frac{1}{{10}}$ số học sinh giỏi Tiếng Anh bằng $\frac{6}{{83}}$ số học sinh giỏi Toán nên $\frac{6}{{60}}$ số học sinh giỏi Tiếng Anh bằng $\frac{6}{{83}}$ số học sinh giỏi Toán.
Coi số học sinh giỏi Tiếng Anh là 60 phần thì số học sinh giỏi Toán là 83 phần.
Hiệu số phần bằng nhau là 83 – 60 = 23 (phần)
Vì 47 không chia hết cho 23 và 92 chia hết cho 23 nên số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là 92 bạn.
Số học sinh giỏi Toán là 92 : 23 x 83 = 332 (học sinh)
Số học sinh giỏi Tiếng Anh là 92 : 23 x 60 = 240 (học sinh)
Đáp số: Học sinh giỏi Toán: 332 học sinh
Học sinh giỏi Tiếng Anh: 240 học sinh
ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS CẦU GIẤY
NĂM HỌC 2022 – 2023
Thời gian làm bài: 45 phút
Phần 1: Trắc nghiệm(Mỗi câu hỏi 0,75 điểm)
Câu 1. Tính: $3,5 \times \frac{1}{4} - 1,5 \times \frac{1}{4}$
A. 0
B. $\frac{1}{2}$
C. $\frac{5}{4}$
D. $\frac{1}{8}$
Câu 2. 0,2 m3 gấp 25 dm3 số lần là
A. 0,008
B. 0,8
C. 8
D. 80
Câu 3. Một ô tô đi với vận tốc 60 km/giờ, tính quãng đường ô tô đi được trong 12 phút.
A. 0,2 km
B. 5 km
C. 720 km
D. 12 km
Câu 4. Một hình hộp hình chữ nhật có chiều dài là 12 cm, chiều rộng là 8 cm. Một hình lập phương có cạnh bằng trung bình cộng ba kích thước của hình hộp chữ nhật và có diện tích toàn phần là 486 cm2. Tìm chiều cao của hình hộp chữ nhật.
A. 7 cm
B. 8 cm
C. 9 cm
D. 81 cm
Phần 2: Điền đáp số (Mỗi câu 1 điềm)
Câu 5. Tìm $x$, biết: $15,25 - 5 \times x = 0,75$
Trả lời: ......................
Câu 6. Tổng số học sinh khối 5 của một trường tiểu học là một số có ba chữ số và chữ số hàng trăm là 2. Biết khi xếp học sinh thành 10 hàng thì dư 5 học sinh và xếp thành 9 hàng thì không dư. Hỏi số học sinh khối 5 là bao nhiêu?
Trả lời: .................
Câu 7. Tuổi anh bằng $\frac{5}{4}$ tuổi em. Biết hai lần tuổi anh cộng với tuổi em là 28 tuổi. Tính số tuổi của anh.
Trả lời: ......................
Câu 8. Cho hình thang ABCD có hai đáy AB, CD. Hai đường chéo AC và BD cắt nhau tại O. Biết diện tích tam giác OAD là 11 cm2, diện tích tam giác OAB là 5 cm2. Tính diện tích hình thang ABCD.
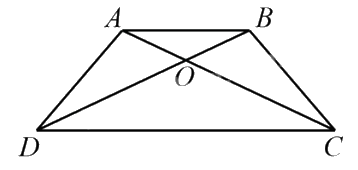
Trả lời: .......................
Phần 3: Tự luận
Bài 1 (2 điểm). Một cuộc thi vẽ có 120 học sinh đạt giải. Số học sinh đạt giải nhất bằng 10% tổng số học sinh đạt giải, số học sinh đạt giải nhì bằng $\frac{1}{5}$ tổng số học sinh đạt ba giải còn lại, số học sinh đạt giải ba bằng $\frac{3}{5}$ số học sinh đạt giải khuyến khích.
a) Tính số học sinh đạt giải nhất.
b) Tính số học sinh đạt giải khuyến khích
Bài 2 (1 điểm). Trong kì thi chọn HSG có 2 môn thi là Toán và Tiếng Anh. Biết $\frac{1}{{10}}$ số học sinh giỏi Tiếng Anh bằng $\frac{6}{{83}}$ số học sinh giỏi Toán. Số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là một số có hai chữ số, chia cho 5 và 9 đều dư 2. Tính số học sinh giỏi Toán, số học sinh giỏi Tiếng Anh.
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1. Trắc nghiệm
Câu 1
$3,5 \times \frac{1}{4} - 1,5 \times \frac{1}{4} = (3,5 - 1,5) \times \frac{1}{4} = 2 \times \frac{1}{4} = \frac{1}{2}$
Chọn B
Câu 2
Đổi 0,2 m3 = 200 dm3
0,2 m3 gấp 25 dm3 số lần là 200 : 25 = 8 (lần)
Chọn C
Câu 3
Đổi 12 phút = $\frac{1}{5}$ giờ
Quãng đường ô tô đi được trong 12 phút là $60 \times \frac{1}{5} = 12$ (km)
Chọn D
Câu 4
Diện tích một mặt của hình lập phương là 486 : 6 = 81 (cm2)
Vì 81 = 9 x 9 nên cạnh hình lập phương có độ dài là 9 cm
Tổng độ dài 3 kích thước của hình hộp chữ nhật là 9 x 3 = 27 (cm)
Chiều cao của hình hộp chữ nhật là 27 – 12 – 8 = 7 (cm)
Chọn A
Phần 2. Điền đáp số
Câu 5
$15,25 - 5 \times x = 0,75$
$5 \times x = 15,25 - 0,75$
$5 \times x = 14,5$
$x = 14,5:5$
$x = 2,9$
Câu 6
Gọi số học sinh của khối 5 là $\overline {2ab} $
Vì khi xếp học sinh thành 10 hàng thì dư 5 học sinh nên số học sinh là số chia 10 dư 5
Suy ra b = 5
Vì số học sinh xếp thành 9 hàng thì không dư nên $\overline {2a5} $ chia hết cho 9.
Suy ra (2 + a + 5) chia hết cho 9 nên a = 2
Vậy khối 5 có 225 học sinh.
Câu 7
Coi tuổi anh là 5 phần thì tuổi em là 4 phần.
Khi đó, 2 lần tuổi anh là 10 phần.
28 tuổi ứng với: 10 + 4 = 14 (phần)
Tuổi anh là 28 : 14 x 5 = 10 (tuổi)
Đáp số: 10 tuổi
Câu 8
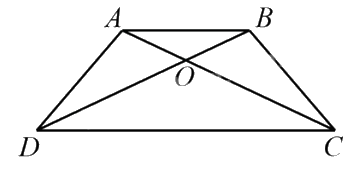
${S_{CAB}} = {S_{DAB}}$ (Chung đáy AB và chiều cao bằng nhau)
Mà ${S_{DAB}} = {S_{OAB}} + {S_{OAD}} = 5 + 11 = 16$ (cm2) nên ${S_{CAB}} = 16$ cm2
$ \Rightarrow {S_{OBC}} = {S_{CAB}} - {S_{OAB}} = 16 - 5 = 11$ (cm2)
Ta có $\frac{{{S_{AOB}}}}{{{S_{AOD}}}} = \frac{{OB}}{{OD}} = \frac{5}{{11}}$ (Hai tam giác có chung chiều cao hạ từ A xuống BD)
Ta có $\frac{{{S_{OBC}}}}{{{S_{ODC}}}} = \frac{{OB}}{{OD}}$ (Hai tam giác có chung chiều cao hạ từ C xuống đáy BD)
Suy ra $\frac{{11}}{{{S_{ODC}}}} = \frac{5}{{11}}$ $ \Rightarrow $ SODC = 11 x 11 : 5 = 24,2 (cm2)
SABCD = SABD + SOBC + SODC = 16 + 11 + 24,2 = 51,2 (cm2)
Đáp số: 51,2 cm2
Phần 3: Tự luận
Bài 1
a) Số học sinh đạt giải nhất
120 x 10 : 100 = 12 (học sinh)
b) Vì số học sinh đạt giải nhì bằng $\frac{1}{5}$ tổng số học sinh đạt ba giải còn lại nên số học sinh đạt giải nhì bằng $\frac{1}{6}$ tổng số học sinh đạt giải.
Số học sinh đạt giải nhì là
$120 \times \frac{1}{6} = 20$ (học sinh)
Tổng số học sinh đạt giải ba và giải khuyến khích là
120 – 12 – 20 = 88 (học sinh)
Số học sinh đạt giải khuyến khích là
88 : (3 + 5) x 5 = 55 (học sinh)
Đáp số: a) 12 học sinh;
b) 55 học sinh
Bài 2
Các số có hai chữ số chia cho 5 và 9 đều dư 2 là 47 và 92.
Do đó số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là 47 bạn và 92 bạn.
Biết $\frac{1}{{10}}$ số học sinh giỏi Tiếng Anh bằng $\frac{6}{{83}}$ số học sinh giỏi Toán nên $\frac{6}{{60}}$ số học sinh giỏi Tiếng Anh bằng $\frac{6}{{83}}$ số học sinh giỏi Toán.
Coi số học sinh giỏi Tiếng Anh là 60 phần thì số học sinh giỏi Toán là 83 phần.
Hiệu số phần bằng nhau là 83 – 60 = 23 (phần)
Vì 47 không chia hết cho 23 và 92 chia hết cho 23 nên số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là 92 bạn.
Số học sinh giỏi Toán là 92 : 23 x 83 = 332 (học sinh)
Số học sinh giỏi Tiếng Anh là 92 : 23 x 60 = 240 (học sinh)
Đáp số: Học sinh giỏi Toán: 332 học sinh
Học sinh giỏi Tiếng Anh: 240 học sinh
Kỳ thi tuyển sinh vào lớp 6 trường Cầu Giấy luôn được đánh giá là một trong những kỳ thi có độ cạnh tranh cao nhất tại Hà Nội. Do đó, việc chuẩn bị kỹ lưỡng và có kế hoạch ôn luyện bài bản là vô cùng cần thiết. Đề thi vào lớp 6 môn Toán trường Cầu Giấy thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải nắm vững kiến thức cơ bản và có khả năng vận dụng linh hoạt vào giải quyết các bài toán thực tế.
Cấu trúc đề thi thường bao gồm các phần chính sau:
Các dạng bài tập thường xuất hiện trong đề thi:
Việc luyện tập với đề thi thử đóng vai trò quan trọng trong quá trình chuẩn bị cho kỳ thi tuyển sinh. Đề thi thử giúp học sinh:
Để giải các bài tập về số học, học sinh cần nắm vững các quy tắc tính toán và các khái niệm cơ bản. Ví dụ, để giải bài toán tìm ước chung lớn nhất (UCLN) của hai số, học sinh có thể sử dụng phương pháp phân tích thành thừa số nguyên tố.
Đối với các bài tập về hình học, học sinh cần hiểu rõ các công thức tính diện tích, chu vi và các tính chất của các hình. Ví dụ, để tính diện tích hình chữ nhật, học sinh cần biết công thức: Diện tích = Chiều dài x Chiều rộng.
Để giải các bài toán có lời văn, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, học sinh cần phân tích đề bài và tìm ra mối liên hệ giữa các yếu tố để xây dựng phương án giải phù hợp.
Giaitoan.edu.vn tự hào là một trong những website hàng đầu về giải toán online tại Việt Nam. Chúng tôi cung cấp đầy đủ các tài liệu ôn thi, đề thi thử và các bài giảng chất lượng cao, giúp học sinh tự tin bước vào kỳ thi tuyển sinh vào lớp 6. Hãy đồng hành cùng chúng tôi để đạt được kết quả tốt nhất!
| Dạng bài tập | Mức độ khó | Phương pháp giải |
|---|---|---|
| Số học | Dễ - Trung bình | Quy tắc tính toán, phân tích thừa số nguyên tố |
| Hình học | Trung bình | Công thức tính diện tích, chu vi, tính chất hình |
| Giải toán có lời văn | Trung bình - Khó | Phân tích đề bài, xây dựng phương án giải |