Giaitoan.edu.vn xin giới thiệu bộ đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2019. Đây là tài liệu vô cùng hữu ích dành cho các em học sinh đang chuẩn bị bước vào kỳ thi quan trọng này.
Bộ đề thi này được biên soạn dựa trên cấu trúc đề thi chính thức của trường, giúp các em làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề.
Có bao nhiêu số có 2 chữ số mà số đó gấp 4 lần tổng 2 chữ số của nó? Người ta xây một bể nước, chiều dài 15m, chiều rộng 10 m, một khu có độ sâu 0,8 m ...
ĐỀ THI VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM HỌC 2019 - 2020
MÔN: TOÁN
PHẦN 1: TRẮC NGHIỆM
Bài 1. An nghĩ ra một số, Bình nghĩ ra một số bằng $\frac{4}{3}$ số của An. Cường nghĩ ra một số bằng 60% số của Bình. Hỏi số của Cường bằng bao nhiêu phần trăm số của An?
A. 60%
B. 80%
C. 70%
D. 90%
Bài 2. Có bao nhiêu số có 2 chữ số mà số đó gấp 4 lần tổng 2 chữ số của nó?
A. 2
B. 3
C. 4
D. 5
Bài 3. Năm nay tuổi bố gấp 8 lần tuổi bé An, tuổi mẹ gấp 7 lần tuổi bé An và bố hơn mẹ 4 tuổi. Hỏi sang năm bé An bao nhiêu tuổi?
A. 4
B. 3
C. 5
D. 6
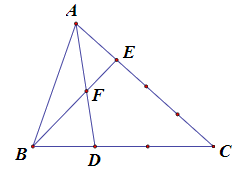
Bài 4. Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF.
A. 2
B. 1,5
C. 3
D. 1
Bài 5. Người thứ nhất làm xong công việc trong 5 giờ, người thứ hai làm xong công việc trong 4 giờ. Hỏi cả hai người cùng làm mất bao lâu?
A. 20 giờ
B. 9 giờ
C. $\frac{7}{{20}}$ giờ
D. $\frac{{20}}{9}$ giờ
Bài 6. Người ta xây một bể nước, chiều dài 15m, chiều rộng 10 m, một khu có độ sâu 0,8 m, 1 khu có độ sâu 1 m, hai khu có diện tích mặt nước bằng nhau. Hỏi muốn mặt nước cách mặt bể 10 cm thì phải xả vào bao nhiêu m3 nước, biết bể chưa có nước.
A. 52,5 m3
B. 67,5 m3
C. 100 m3
D. 120 m3
PHẦN 2: TỰ LUẬN
Bài 7. Có 3 can dầu. Sau khi can một cho can hai 2 lít, can hai cho can ba 3 lít thì số dầu can một bằng $\frac{2}{9}$ tổng số dầu và can hai có số dầu bằng 75% số dầu can ba. Hỏi lúc đầu mỗi can có bao nhiêu lít dầu biết sau khi chuyển thì can ba nhiều hơn can một là 8 lít.
Bài 8. Quãng đường AB dài 60km. Cùng lúc có xe đi từ A và từ B khởi hành. Sau $2\frac{2}{9}$ giờ thì chúng gặp nhau. Nếu vận tốc xe đi từ B tăng thêm 3km/giờ thì hai xe sẽ gặp nhau ở chính giữa quãng đường AB. Tính vận tốc mỗi xe lúc đầu.
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Bài 1. An nghĩ ra một số, Bình nghĩ ra một số bằng $\frac{4}{3}$ số của An. Cường nghĩ ra một số bằng 60% số của Bình. Hỏi số của Cường bằng bao nhiêu phần trăm số của An?
A. 60%
B. 80%
C. 70%
D. 90%
Cách giải
Gọi số An nghĩ là A
Số Bình nghĩ là $\frac{4}{3} \times A$
Số Cường nghĩ là $\frac{3}{5} \times \frac{4}{3} \times A = \frac{4}{5} \times A$ = 0,8 x A = 80% x A
Chọn B
Bài 2. Có bao nhiêu số có 2 chữ số mà số đó gấp 4 lần tổng 2 chữ số của nó?
A. 2
B. 3
C. 4
D. 5
Cách giải
Gọi số cần tìm là $\overline {ab} $ (a khác 0)
Ta có $\overline {ab} = 4 \times (a + b)$
$10 \times a + b = 4 \times a + 4 \times b$
$6 \times a = 3 \times b$
$2 \times a = b$
Nếu a = 1 thì b = 2, ta được số 12
Nếu a = 2 thì b = 4 ta được số 24
Nếu a = 3 thì b = 6 ta được số 36
Nếu a = 4 thì b = 8 ta được số 48
Vậy có 4 số thỏa mãn đề bài.
Chọn C
Bài 3. Năm nay tuổi bố gấp 8 lần tuổi bé An, tuổi mẹ gấp 7 lần tuổi bé An và bố hơn mẹ 4 tuổi. Hỏi sang năm bé An bao nhiêu tuổi?
A. 4
B. 3
C. 5
D. 6
Cách giải
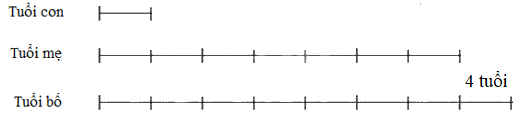
Tuổi bé An năm nay là 4 (tuổi)
Vậy sang năm bé An 5 tuổi.
Chọn C
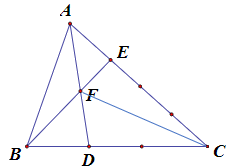
Bài 4. Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF.
A. 2
B. 1,5
C. 3
D. 1
Cách giải:
Nối F với C
Ta có SABE = $\frac{1}{3}$ x SBEC (Chung chiều cao hạ từ đỉnh B và AE = $\frac{1}{3}$ EC)
Và SFAE = $\frac{1}{3}$ x SFEC (Chung chiều cao hạ từ đỉnh F và AE = $\frac{1}{3}$ EC)
$ \Rightarrow $ SBAF = $\frac{1}{3}$ x SBCF
Ta có SBFD = $\frac{1}{3}$ x SBFC (Chung chiều cao hạ từ đỉnh F và BD = $\frac{1}{3}$ x BC)
$ \Rightarrow $ SBAF = SBFD (1)
Ta có SAFB = $\frac{1}{2}$ x SAFC
SAFE = $\frac{1}{4}$ x SAFC (Chung chiều cao hạ từ đỉnh F và và AE = $\frac{1}{4}$ x AC)
$ \Rightarrow $ SAFE = $\frac{1}{2}$ x SBAF (2)
Từ (1) và (2) suy ra SBFD = 2 x SAEF
Chọn A.
Bài 5. Người thứ nhất làm xong công việc trong 5 giờ, người thứ hai làm xong công việc trong 4 giờ. Hỏi cả hai người cùng làm mất bao lâu?
A. 20 giờ
B. 9 giờ
C. $\frac{7}{{20}}$ giờ
D. $\frac{{20}}{9}$ giờ
Cách giải
Trong 1 giờ người thứ nhất làm được số phần công việc là $1:5 = \frac{1}{5}$ (công việc)
Trong 1 giờ người thứ hai làm được số phần công việc là $1:4 = \frac{1}{4}$ (công việc)
Trong 1 giờ cả hai người cùng làm được số phần công việc là $\frac{1}{5} + \frac{1}{4} = \frac{9}{{20}}$ (công việc)
Cả hai người cùng làm thì hoàn thành công việc trong số giờ là $1:\frac{9}{{20}} = \frac{{20}}{9}$ (giờ)
Chọn D
Bài 6. Người ta xây một bể nước, chiều dài 15m, chiều rộng 10 m, một khu có độ sâu 0,8 m,1 khu có độ sâu 1 m, hai khu có diện tích mặt nước bằng nhau. Hỏi muốn mặt nước cách mặt bể 10 cm thì phải xả vào bao nhiêu m3 nước, biết bể chưa có nước.
A. 52,5 m3
B. 67,5 m3
C. 100 m3
D. 120 m3
Cách giải
Đổi 10 cm = 0,1 m
Để mặt nước cách mặt bể 10 cm thì phải xả vào số m3 nước là:
15 x 5 x 0,7 + 15 x 5 x 0,9 = 120 (m3)
Đáp số: 120 m3
Chọn D
PHẦN 2: TỰ LUẬN
Bài 7. Có 3 can dầu. Sau khi can một cho can hai 2 lít, can hai cho can ba 3 lít thì số dầu can một bằng $\frac{2}{9}$ tổng số dầu và can hai có số dầu bằng 75% số dầu can ba. Hỏi lúc đầu mỗi can có bao nhiêu lít dầu biết sau khi chuyển thì can ba nhiều hơn can một là 8 lít.
Cách giải
Sau khi cho nhận thìsố dầu can hai = 75% số dầu can ba = $\frac{3}{4}$ số dầu can ba
Ta có sơ đồ sau khi cho nhận:
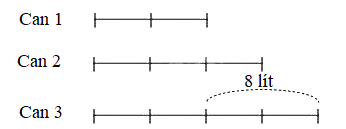
Số lít dầu của mỗi can sau khi cho nhận là: Can 1 có 8 lít, can 2 có 12 lít, can 3 có 16 lít
Số lít dầu của can 1 lúc đầu là 8 + 2 = 10 (lít)
Số lít dầu của can 2 lúc đầu là 12 – 2 + 3 = 13 (lít)
Số lít dầu của can 3 lúc đầu là 16 – 3 = 13 (lít)
Đáp số: Can 1: 10 lít
Can 2: 13 lít
Can 3: 13 lít
Bài 8. Quãng đường AB dài 60km. Cùng lúc có xe đi từ A và từ B khởi hành. Sau $2\frac{2}{9}$ giờ thì chúng gặp nhau. Nếu vận tốc xe đi từ B tăng thêm 3km/giờ thì hai xe sẽ gặp nhau ở chính giữa quãng đường AB. Tính vận tốc mỗi xe lúc đầu.
Cách giải
Gọi vận tốc xe đi từ A là v1, vận tốc xe đi từ B là v2
Tổng vận tốc 2 xe là
$60:2\frac{2}{9} = 27$ (km/giờ)
Biết vận tốc xe đi từ B tăng thêm 3km/giờ thì hai xe sẽ gặp nhau ở chính giữa quãng đường AB, suy ra v1 – v2 = 3
Vận tốc xe đi từ A là (27 + 3) : 2 = 15 (km/giờ)
Vận tốc xe đi từ B là 27 – 15 = 12 (km/giờ)
Đáp số: 15 (km/giờ) ; 12 (km/giờ)
ĐỀ THI VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM HỌC 2019 - 2020
MÔN: TOÁN
PHẦN 1: TRẮC NGHIỆM
Bài 1. An nghĩ ra một số, Bình nghĩ ra một số bằng $\frac{4}{3}$ số của An. Cường nghĩ ra một số bằng 60% số của Bình. Hỏi số của Cường bằng bao nhiêu phần trăm số của An?
A. 60%
B. 80%
C. 70%
D. 90%
Bài 2. Có bao nhiêu số có 2 chữ số mà số đó gấp 4 lần tổng 2 chữ số của nó?
A. 2
B. 3
C. 4
D. 5
Bài 3. Năm nay tuổi bố gấp 8 lần tuổi bé An, tuổi mẹ gấp 7 lần tuổi bé An và bố hơn mẹ 4 tuổi. Hỏi sang năm bé An bao nhiêu tuổi?
A. 4
B. 3
C. 5
D. 6
Bài 4. Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF.
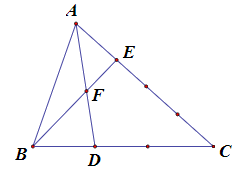
A. 2
B. 1,5
C. 3
D. 1
Bài 5. Người thứ nhất làm xong công việc trong 5 giờ, người thứ hai làm xong công việc trong 4 giờ. Hỏi cả hai người cùng làm mất bao lâu?
A. 20 giờ
B. 9 giờ
C. $\frac{7}{{20}}$ giờ
D. $\frac{{20}}{9}$ giờ
Bài 6. Người ta xây một bể nước, chiều dài 15m, chiều rộng 10 m, một khu có độ sâu 0,8 m, 1 khu có độ sâu 1 m, hai khu có diện tích mặt nước bằng nhau. Hỏi muốn mặt nước cách mặt bể 10 cm thì phải xả vào bao nhiêu m3 nước, biết bể chưa có nước.
A. 52,5 m3
B. 67,5 m3
C. 100 m3
D. 120 m3
PHẦN 2: TỰ LUẬN
Bài 7. Có 3 can dầu. Sau khi can một cho can hai 2 lít, can hai cho can ba 3 lít thì số dầu can một bằng $\frac{2}{9}$ tổng số dầu và can hai có số dầu bằng 75% số dầu can ba. Hỏi lúc đầu mỗi can có bao nhiêu lít dầu biết sau khi chuyển thì can ba nhiều hơn can một là 8 lít.
Bài 8. Quãng đường AB dài 60km. Cùng lúc có xe đi từ A và từ B khởi hành. Sau $2\frac{2}{9}$ giờ thì chúng gặp nhau. Nếu vận tốc xe đi từ B tăng thêm 3km/giờ thì hai xe sẽ gặp nhau ở chính giữa quãng đường AB. Tính vận tốc mỗi xe lúc đầu.
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Bài 1. An nghĩ ra một số, Bình nghĩ ra một số bằng $\frac{4}{3}$ số của An. Cường nghĩ ra một số bằng 60% số của Bình. Hỏi số của Cường bằng bao nhiêu phần trăm số của An?
A. 60%
B. 80%
C. 70%
D. 90%
Cách giải
Gọi số An nghĩ là A
Số Bình nghĩ là $\frac{4}{3} \times A$
Số Cường nghĩ là $\frac{3}{5} \times \frac{4}{3} \times A = \frac{4}{5} \times A$ = 0,8 x A = 80% x A
Chọn B
Bài 2. Có bao nhiêu số có 2 chữ số mà số đó gấp 4 lần tổng 2 chữ số của nó?
A. 2
B. 3
C. 4
D. 5
Cách giải
Gọi số cần tìm là $\overline {ab} $ (a khác 0)
Ta có $\overline {ab} = 4 \times (a + b)$
$10 \times a + b = 4 \times a + 4 \times b$
$6 \times a = 3 \times b$
$2 \times a = b$
Nếu a = 1 thì b = 2, ta được số 12
Nếu a = 2 thì b = 4 ta được số 24
Nếu a = 3 thì b = 6 ta được số 36
Nếu a = 4 thì b = 8 ta được số 48
Vậy có 4 số thỏa mãn đề bài.
Chọn C
Bài 3. Năm nay tuổi bố gấp 8 lần tuổi bé An, tuổi mẹ gấp 7 lần tuổi bé An và bố hơn mẹ 4 tuổi. Hỏi sang năm bé An bao nhiêu tuổi?
A. 4
B. 3
C. 5
D. 6
Cách giải
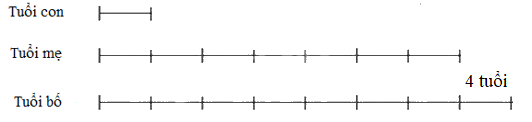
Tuổi bé An năm nay là 4 (tuổi)
Vậy sang năm bé An 5 tuổi.
Chọn C
Bài 4. Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF.
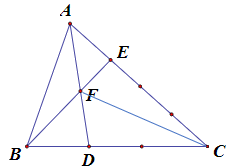
A. 2
B. 1,5
C. 3
D. 1
Cách giải:
Nối F với C
Ta có SABE = $\frac{1}{3}$ x SBEC (Chung chiều cao hạ từ đỉnh B và AE = $\frac{1}{3}$ EC)
Và SFAE = $\frac{1}{3}$ x SFEC (Chung chiều cao hạ từ đỉnh F và AE = $\frac{1}{3}$ EC)
$ \Rightarrow $ SBAF = $\frac{1}{3}$ x SBCF
Ta có SBFD = $\frac{1}{3}$ x SBFC (Chung chiều cao hạ từ đỉnh F và BD = $\frac{1}{3}$ x BC)
$ \Rightarrow $ SBAF = SBFD (1)
Ta có SAFB = $\frac{1}{2}$ x SAFC
SAFE = $\frac{1}{4}$ x SAFC (Chung chiều cao hạ từ đỉnh F và và AE = $\frac{1}{4}$ x AC)
$ \Rightarrow $ SAFE = $\frac{1}{2}$ x SBAF (2)
Từ (1) và (2) suy ra SBFD = 2 x SAEF
Chọn A.
Bài 5. Người thứ nhất làm xong công việc trong 5 giờ, người thứ hai làm xong công việc trong 4 giờ. Hỏi cả hai người cùng làm mất bao lâu?
A. 20 giờ
B. 9 giờ
C. $\frac{7}{{20}}$ giờ
D. $\frac{{20}}{9}$ giờ
Cách giải
Trong 1 giờ người thứ nhất làm được số phần công việc là $1:5 = \frac{1}{5}$ (công việc)
Trong 1 giờ người thứ hai làm được số phần công việc là $1:4 = \frac{1}{4}$ (công việc)
Trong 1 giờ cả hai người cùng làm được số phần công việc là $\frac{1}{5} + \frac{1}{4} = \frac{9}{{20}}$ (công việc)
Cả hai người cùng làm thì hoàn thành công việc trong số giờ là $1:\frac{9}{{20}} = \frac{{20}}{9}$ (giờ)
Chọn D
Bài 6. Người ta xây một bể nước, chiều dài 15m, chiều rộng 10 m, một khu có độ sâu 0,8 m,1 khu có độ sâu 1 m, hai khu có diện tích mặt nước bằng nhau. Hỏi muốn mặt nước cách mặt bể 10 cm thì phải xả vào bao nhiêu m3 nước, biết bể chưa có nước.
A. 52,5 m3
B. 67,5 m3
C. 100 m3
D. 120 m3
Cách giải
Đổi 10 cm = 0,1 m
Để mặt nước cách mặt bể 10 cm thì phải xả vào số m3 nước là:
15 x 5 x 0,7 + 15 x 5 x 0,9 = 120 (m3)
Đáp số: 120 m3
Chọn D
PHẦN 2: TỰ LUẬN
Bài 7. Có 3 can dầu. Sau khi can một cho can hai 2 lít, can hai cho can ba 3 lít thì số dầu can một bằng $\frac{2}{9}$ tổng số dầu và can hai có số dầu bằng 75% số dầu can ba. Hỏi lúc đầu mỗi can có bao nhiêu lít dầu biết sau khi chuyển thì can ba nhiều hơn can một là 8 lít.
Cách giải
Sau khi cho nhận thìsố dầu can hai = 75% số dầu can ba = $\frac{3}{4}$ số dầu can ba
Ta có sơ đồ sau khi cho nhận:
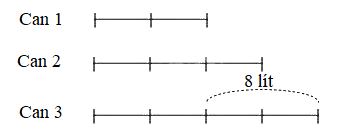
Số lít dầu của mỗi can sau khi cho nhận là: Can 1 có 8 lít, can 2 có 12 lít, can 3 có 16 lít
Số lít dầu của can 1 lúc đầu là 8 + 2 = 10 (lít)
Số lít dầu của can 2 lúc đầu là 12 – 2 + 3 = 13 (lít)
Số lít dầu của can 3 lúc đầu là 16 – 3 = 13 (lít)
Đáp số: Can 1: 10 lít
Can 2: 13 lít
Can 3: 13 lít
Bài 8. Quãng đường AB dài 60km. Cùng lúc có xe đi từ A và từ B khởi hành. Sau $2\frac{2}{9}$ giờ thì chúng gặp nhau. Nếu vận tốc xe đi từ B tăng thêm 3km/giờ thì hai xe sẽ gặp nhau ở chính giữa quãng đường AB. Tính vận tốc mỗi xe lúc đầu.
Cách giải
Gọi vận tốc xe đi từ A là v1, vận tốc xe đi từ B là v2
Tổng vận tốc 2 xe là
$60:2\frac{2}{9} = 27$ (km/giờ)
Biết vận tốc xe đi từ B tăng thêm 3km/giờ thì hai xe sẽ gặp nhau ở chính giữa quãng đường AB, suy ra v1 – v2 = 3
Vận tốc xe đi từ A là (27 + 3) : 2 = 15 (km/giờ)
Vận tốc xe đi từ B là 27 – 15 = 12 (km/giờ)
Đáp số: 15 (km/giờ) ; 12 (km/giờ)
Kỳ thi vào lớp 6 trường chuyên Ngoại ngữ là một bước ngoặt quan trọng trong quá trình học tập của các em. Để đạt được kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Một trong những cách hiệu quả nhất là luyện tập với các đề thi thử, đặc biệt là đề thi chính thức của các năm trước.
Đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2019 thường bao gồm các dạng bài sau:
Để ôn tập hiệu quả cho kỳ thi này, các em cần nắm vững các kiến thức sau:
Dưới đây là một số dạng bài thường xuất hiện trong đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2019:
Để đạt được kết quả tốt nhất trong kỳ thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2019, các em cần lưu ý những điều sau:
Ngoài bộ đề thi này, các em có thể tham khảo thêm các tài liệu ôn tập sau:
Đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2019 là một kỳ thi quan trọng, đòi hỏi sự chuẩn bị kỹ lưỡng. Hy vọng rằng bộ đề thi này cùng với những lời khuyên trên sẽ giúp các em tự tin và đạt được kết quả tốt nhất. Chúc các em thành công!