Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 6 môn Toán trường Archimedes năm 2021 (bài nâng cao). Đây là tài liệu ôn luyện vô cùng quan trọng dành cho các em học sinh đang chuẩn bị bước vào kỳ thi đầy thử thách này.
Bộ đề thi này được biên soạn dựa trên cấu trúc đề thi chính thức của trường Archimedes, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải toán một cách hiệu quả.
Một số tự nhiên được gọi là số tiến nếu các chữ số của nó đôi một khác nhau và chữ số liền sau lớn hơn chữ số liền trước.Một hình chữ nhật có chu vi 200 cm. Người ta giảm chiều dài và chiều rộng đi cùng một độ dài thì được một hình chữ nhật mới có chu vi là 160 cm
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Câu 1. Tính giá trị của biểu thức:
A = 77 x 5,55 + 60,12 x 7,45 + 16,88 x 7,45
Cách giải:
A = 77 x 5,55 + 60,12 x 7,45 + 16,88 x 7,45
A = 77 x 5,55 + 7,45 x (60,12 + 16,88)
A = 77 x 5,55 + 7,45 x 77
A = 77 x (5,55 + 7,45)
A = 77 x 13
A = 1001
Câu 2. Tìm số tự nhiên n biết rằng:
$\left( {1 + \frac{1}{1}} \right) \times \left( {1 + \frac{1}{2}} \right) \times \left( {1 + \frac{1}{3}} \right) \times .... \times \left( {1 + \frac{1}{n}} \right) = 2070$
Cách giải:
$\left( {1 + \frac{1}{1}} \right) \times \left( {1 + \frac{1}{2}} \right) \times \left( {1 + \frac{1}{3}} \right) \times .... \times \left( {1 + \frac{1}{n}} \right) = 2070$
$\frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \times .... \times \frac{{n + 1}}{n} = 2070$
$n + 1 = 2070$
$n = 2069$
Câu 3. Một số tự nhiên được gọi là số tiến nếu các chữ số của nó đôi một khác nhau và chữ số liền sau lớn hơn chữ số liền trước. Ví dụ: 13579 và 24689 là các số tiến; nhưng 11345 không phải là số tiến. Hỏi trong các số tự nhiên từ 2021 đến 2401, có bao nhiêu số là số tiến?
Cách giải:
Các số tiến từ 2021 đến 2401 gồm có 2345 đến 2349 (5 số), 2356 đến 2359 (4 số), 2367, 2368, 2369, 2378, 2379, 2389)
Vậy có 15 số tiến từ 2021 đến 2401.
Câu 4. Một hình chữ nhật có chu vi 200 cm. Người ta giảm chiều dài và chiều rộng đi cùng một độ dài thì được một hình chữ nhật mới có chu vi là 160 cm. Hỏi diện tích của phần giảm đi là bao nhiêu?
Cách giải:
Nửa chu vi ban đầu là: 200 : 2 = 100 (cm) Nửa chu vi lúc sau: 160 : 2 = 80 (cm) Chiều dài và chiều rộng cùng giảm đi: (100 – 80) : 2 = 10 (cm) Phần diện tích giảm đi là: (100 – 10) x 10 = 900 (cm2)
Đáp số: 900cm2
Câu 5. Cách đây 6 năm, tổng số tuổi của Nam và anh trai Nam là 18 tuổi. Hiện tại, số tuổi của Nam bằng $\frac{2}{3}$ số tuổi của anh trai Nam. Hỏi hiện tại Nam bao nhiêu tuổi?
Cách giải:
Tổng số tuổi của Nam và anh trai Nam hiện này là:
18 + 6 + 6 = 30 (tuổi)
Tuổi của Nam hiện nay là:
30 : (2 + 3) x 2 = 12 (tuổi)
Đáp số: 12 tuổi
Câu 6. Vào ngày 18/04/2021, một cửa hàng thịt treo biển khuyến mãi: “Duy nhất ngày hôm nay, thăn bò Úc giảm 40%, chỉ 117000 đồng nửa ký!”. Hỏi, giá thịt thăn bò Úc tại cửa hàng đó trước khi khuyến mãi là bao nhiêu một kg (tính theo đồng)?
Cách giải:
Giá một kg thịt bò sau khi giảm 40% là:
117000 x 2 = 234000 (đồng)
Giá 1 kg thịt thăn bò Úc tại cửa hàng đó trước khi khuyến mãi là:
234000 : 60 x 100 = 390000 (đồng)
Đáp số: 390000 đồng
Câu 7. Xét biểu thức:
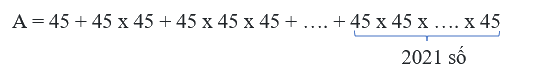
Hỏi khi tính giá trị biểu thức A, giá trị thu được có chữ số hàng đơn vị là bao nhiêu?
Cách giải:
A có 2021 số hạng, mỗi số hạng đều có chữ số hàng đơn vị là 5.
Suy ra A có chữ số hàng đơn vị là hàng đơn vị của tích 5 x 2021.
Vậy A có chữ số tận cùng là 5.
Câu 8. Trong dãy 15 ô vuông bên dưới, người ta điền vào mỗi ô vuông một số tự nhiên sao cho tổng các số ở ba ô liên tiếp bất kỳ luôn bằng 39. Tìm số được điền vào ô vuông tô đậm.

Cách giải:
Ô thứ 3 trong dãy là 11.
Suy ra ô thứ hai trong dãy là: 39 – 20 – 11 = 8
Vì tổng các số ở ba ô liên tiếp bất kỳ luôn bằng 39 nên các số lặp lại theo thứ tự 20, 8, 11.
Vậy số điền vào ô màu xanh là số 8.
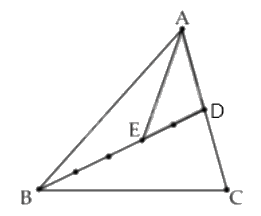
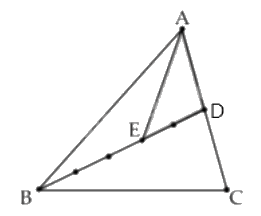
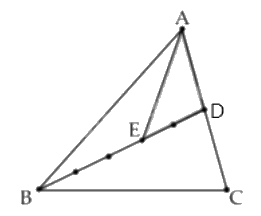
Câu 9. Trong hình vẽ dưới, D là điểm trên cạnh AC của tam giác ABC và AD = DC; E là điểm trên đoạn BD thỏa mãn BE : BD = 3 : 5. Biết rằng diện tích tam giác ADE là 96 cm2. Tính diện tích tam giác ABC.
Cách giải:
$\frac{{{S_{ABD}}}}{{{S_{ADE}}}} = \frac{5}{2}$ (Hai tam giác có chung chiều cao hạ từ đỉnh A và đáy $BD = \frac{5}{2}DE$)
Suy ra ${S_{ABD}} = \frac{5}{2} \times {S_{ADE}} = \frac{5}{2} \times 96 = 240$ (cm2)
Ta có ${S_{ABC}} = 2 \times {S_{ABD}}$ (Hai tam giác có chung chiều cao hạ từ B và đáy AC = 2 x AD)
Vậy ${S_{ABC}} = 240 \times 2 = 480$(cm2)
Câu 10. Nam có bốn quyển sách gồm Toán, Tiếng Việt, Tiếng Anh và Lịch Sử. Nam muốn xếp bốn quyển sách này lên một kệ sách trống sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau. Hỏi có bao nhiêu cách xếp?
Cách giải:
Cách cách xếp sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau là:
Toán, Tiếng Việt, Tiếng Anh, Lịch sử
Toán, Tiếng Việt, Lịch sử, Tiếng Anh
Toán, Tiếng Anh, Tiếng Việt, Lịch sử
Toán, Tiếng Anh, Lịch sử, Tiếng Việt
Tiếng Việt, Toán, Tiếng Anh, Lịch sử
Tiếng Việt, Lịch sử, Tiếng Anh, Toán
Tiếng Anh, Toán, Tiếng Việt, Lịch sử
Tiếng Anh, Lịch sử, Tiếng Việt, Toán
Lịch sử, tiếng Anh, Tiếng Việt, Toán
Lịch sử, Tiếng Anh, Toán, Tiếng Việt
Lịch sử, Tiếng Việt, Tiếng Anh, Toán
Lịch sử, Tiếng Việt, Toán, Tiếng Anh
Vậy có 12 cách xếp.
PHẦN II. TỰ LUẬN
Câu 11. Trong một cuộc thi, có năm thí sinh tham dự A, B, C, D và E. Trước khi cuộc thi diễn ra, có bốn dự đoán về kết quả xếp hạng của năm thí sinh như sau:
Kết thúc cuộc thi, người ta nhận thấy mỗi người dự đoán đều đúng cho một thí sinh nào đó và sai cho người còn lại. Biết rằng không có hai thí sinh nào có cùng thứ hạng, hỏi ai đứng thứ ba ở cuộc thi đó?
Cách giải:
Xuất phát từ dự đoán thứ nhất: Nếu B đứng thứ 4 là đúng và E đứng thứ hai là sai, khi đó ở dự đoán thứ 3, E đứng thứ ba sẽ đúng và A đứng thứ 4 sẽ sai. Ở dự đoán thứ tư, A đứng thứ ba sẽ sai và B đứng thứ nhất sẽ đúng (vô lý vì B không thể vừa đứng thứ tư, vừa đứng thứ nhất). Do vậy ở dự đoán thứ nhất, B đứng thứ tư là sai và E đứng thứ hai là đúng. Lúc này ở dự đoán số 3, E đứng thứ ba là sai và A đứng thứ tư đúng. Ở dự đoán thứ tư, A đứng thứ ba sai và B đứng thứ nhất đúng. Ở dự đoán số hai, D đứng nhất sai và C đứng thứ ba đúng. Vậy B đứng thứ nhất, E đứng thứ hai, C đứng thứ ba và A đứng thứ tư.
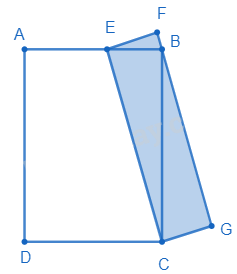
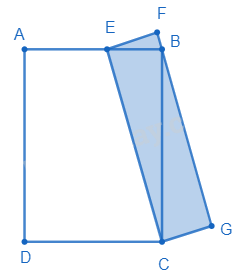
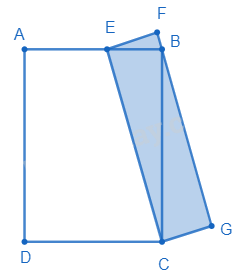
Câu 12. Trong hình vẽ bên dưới, ABDC và CEFG là hai hình chữ nhật, trong đó điểm B nằm trên cạnh FG của hình chữ nhật CEFG và điểm E nằm trên cạnh AB của hình chữ nhật ABCD thỏa mãn AE : EB = 3 : 2. Biết rằng diện tích hình chữ nhật ABCD là 35 cm2, tính diện tích hình chữ nhật CEFG?
Cách giải:
${S_{ABC}} = \frac{1}{2} \times {S_{ABCD}} = \frac{1}{2} \times 35 = \frac{{35}}{2}$(cm2)
Ta có $\frac{{{S_{EBC}}}}{{{S_{ABC}}}} = \frac{2}{5}$ (Hai tam giác có chung chiều cao hạ từ C và $EB = \frac{2}{5}AB$)
Suy ra ${S_{EBC}} = \frac{2}{5} \times \frac{{35}}{2} = 7$ (cm2)
Ta có $SCEFG = 2 \times {S_{EBC}} = 2 \times 7 = 14$ (cm2)
Đáp số: 14 cm2
Câu 13. Cho 16 số tự nhiên phân biệt khác 0 thỏa mãn tích của năm số bất kì trong 16 số này là số chẵn. Gọi S là tổng của 16 số này. Biết rằng S là số lẻ, hỏi S có thể nhận giá trị nhỏ nhất là bao nhiêu?
Cách giải:
Do tích của 5 số bất kỳ luôn chẵn nên số lượng số lẻ tối đa là 4 số lẻ. Ngoài ra do tổng của 16 số này là lẻ nên chỉ có thể có 1 số lẻ hoặc 3 số lẻ. Nếu có 1 số lẻ thì tổng 16 số nhỏ nhất là 1 + 2 + 4 + 6 + 8 + ... + 30 = 241 Nếu có 3 số lẻ thì tổng 16 số nhỏ nhất là 1 + 3 + 5 + 2 + 4 + 6 + ….. + 26 = 191 Vậy tổng S nhỏ nhất là 191
Câu 14. Cho số A = 206920692069…2069 (A gồm 250 số 2069 viết liền nhau). Người ta muốn xóa một số chữ số của số A sao cho số thu được có tổng tất cả các chữ số bằng 2021. Hỏi, có thể xóa được nhiều nhất bao nhiêu chữ số? Khi đó, số lớn nhất có thể thu được là bao nhiêu?
Cách giải:
A đang có tổng các chữ số là (2 + 0 + 6 + 9) x 250 = 4250 Tổng các chữ số cần xóa đi: 4250 – 2021 = 2229. Trước tiên ta xóa hết 250 chữ số 0. Tiếp theo, nhận thấy 2229 chia hết cho 3, các chữ số 6 và 9 cũng chia hết cho 3 nên số lượng chữ số 2 xóa đi cũng phải chia hết cho 3. Có 250 chữ số 2, vậy ta xóa đi 249 chữ số 2. Lúc này tổng các chữ số 6 và 9 cần xóa là: 2229 – 249 x 2 = 1731. Nhận thấy số lượng chữ số 6 cần xóa phải nhiều nhất có thể, có 250 chữ số 6 nên ta thử:
+) Nếu xóa hết 250 chữ số 6 thì tổng các chữ số 9 cần xóa là 1731 – 250 x 6 = 231 không chia hết cho 9. +) Nếu xóa 249 chữ số 6 thì tổng các chữ số 9 cần xóa là 1731 – 249 x 6 = 237 không chia hết cho 9. +) Nếu xóa 248 chữ số 6 thì tổng các chữ số 9 cần xóa là 1731 – 248 x 6 = 243 chia hết cho 9) cần xóa 243 : 9 = 27 chữ số 9. Vậy cần xóa nhiều nhất 250 chữ số 0; 249 chữ số 2; 248 chữ số 6 và 27 chữ số 9, tức là 250 + 249 + 248 + 27 = 774 chữ số. Lúc này còn lại 226 chữ số gồm 1 chữ số 2; 2 chữ số 6 và 223 chữ số 9. Số lớn nhất có thể thu được là 9999… 9999662.
ĐỀ THI VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS ARCHIMEDES
(BÀI NÂNG CAO)
NĂM HỌC 2021 – 2022
Thời gian làm bài: 90 phút
PHẦN 1. TRẮC NGHIỆM
Câu 1. Tính giá trị của biểu thức:
A = 77 x 5,55 + 60,12 x 7,45 + 16,88 x 7,45
Câu 2. Tìm số tự nhiên n biết rằng:
$\left( {1 + \frac{1}{1}} \right) \times \left( {1 + \frac{1}{2}} \right) \times \left( {1 + \frac{1}{3}} \right) \times .... \times \left( {1 + \frac{1}{n}} \right) = 2070$
Câu 3. Một số tự nhiên được gọi là số tiến nếu các chữ số của nó đôi một khác nhau và chữ số liền sau lớn hơn chữ số liền trước. Ví dụ: 13579 và 24689 là các số tiến; nhưng 11345 không phải là số tiến. Hỏi trong các số tự nhiên từ 2021 đến 2401, có bao nhiêu số là số tiến?
Câu 4. Một hình chữ nhật có chu vi 200 cm. Người ta giảm chiều dài và chiều rộng đi cùng một độ dài thì được một hình chữ nhật mới có chu vi là 160 cm. Hỏi diện tích của phần giảm đi là bao nhiêu?
Câu 5. Cách đây 6 năm, tổng số tuổi của Nam và anh trai Nam là 18 tuổi. Hiện tại, số tuổi của Nam bằng $\frac{2}{3}$ số tuổi của anh trai Nam. Hỏi hiện tại Nam bao nhiêu tuổi?
Câu 6. Vào ngày 18/04/2021, một cửa hàng thịt treo biển khuyến mãi: “Duy nhất ngày hôm nay, thăn bò Úc giảm 40%, chỉ 117000 đồng nửa ký!”. Hỏi, giá thịt thăn bò Úc tại cửa hàng đó trước khi khuyến mãi là bao nhiêu một kg (tính theo đồng)?
Câu 7. Xét biểu thức:
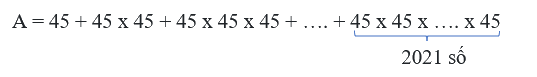
Hỏi khi tính giá trị biểu thức A, giá trị thu được có chữ số hàng đơn vị là bao nhiêu?
Câu 8. Trong dãy 15 ô vuông bên dưới, người ta điền vào mỗi ô vuông một số tự nhiên sao cho tổng các số ở ba ô liên tiếp bất kỳ luôn bằng 39. Tìm số được điền vào ô vuông tô đậm.

Câu 9. Trong hình vẽ dưới, D là điểm trên cạnh AC của tam giác ABC và AD = DC; E là điểm trên đoạn BD thỏa mãn BE : BD = 3 : 5. Biết rằng diện tích tam giác ADE là 96 cm2. Tính diện tích tam giác ABC.
Câu 10. Nam có bốn quyển sách gồm Toán, Tiếng Việt, Tiếng Anh và Lịch Sử. Nam muốn xếp bốn quyển sách này lên một kệ sách trống sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau. Hỏi có bao nhiêu cách xếp?
PHẦN II. TỰ LUẬN
Câu 11. Trong một cuộc thi, có năm thí sinh tham dự là A, B, C, D và E. Trước khi cuộc thi diễn ra, có bốn dự đoán về kết quả xếp hạng của năm thí sinh như sau:
Kết thúc cuộc thi, người ta nhận thấy mỗi người dự đoán đều đúng cho một thí sinh nào đó và sai cho người còn lại. Biết rằng không có hai thí sinh nào có cùng thứ hạng, hỏi ai đứng thứ ba ở cuộc thi đó?
Câu 12. Trong hình vẽ dưới, ABDC và CEFG là hai hình chữ nhật, trong đó điểm B nằm trên cạnh FG của hình chữ nhật CEFG và điểm E nằm trên cạnh AB của hình chữ nhật ABCD thỏa mãn AE : EB = 3 : 2. Biết rằng diện tích hình chữ nhật ABCD là 35 cm2, tính diện tích hình chữ nhật CEFG?
Câu 13. Cho 16 số tự nhiên phân biệt khác 0 thỏa mãn tích của năm số bất kì trong 16 số này là số chẵn. Gọi S là tổng của 16 số này. Biết rằng S là số lẻ, hỏi S có thể nhận giá trị nhỏ nhất là bao nhiêu?
Câu 14. Cho số A = 206920692069…2069 (A gồm 250 số 2069 viết liền nhau). Người ta muốn xóa một số chữ số của số A sao cho số thu được có tổng tất cả các chữ số bằng 2021. Hỏi, có thể xóa được nhiều nhất bao nhiêu chữ số? Khi đó, số lớn nhất có thể thu được là bao nhiêu?
ĐỀ THI VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS ARCHIMEDES
(BÀI NÂNG CAO)
NĂM HỌC 2021 – 2022
Thời gian làm bài: 90 phút
PHẦN 1. TRẮC NGHIỆM
Câu 1. Tính giá trị của biểu thức:
A = 77 x 5,55 + 60,12 x 7,45 + 16,88 x 7,45
Câu 2. Tìm số tự nhiên n biết rằng:
$\left( {1 + \frac{1}{1}} \right) \times \left( {1 + \frac{1}{2}} \right) \times \left( {1 + \frac{1}{3}} \right) \times .... \times \left( {1 + \frac{1}{n}} \right) = 2070$
Câu 3. Một số tự nhiên được gọi là số tiến nếu các chữ số của nó đôi một khác nhau và chữ số liền sau lớn hơn chữ số liền trước. Ví dụ: 13579 và 24689 là các số tiến; nhưng 11345 không phải là số tiến. Hỏi trong các số tự nhiên từ 2021 đến 2401, có bao nhiêu số là số tiến?
Câu 4. Một hình chữ nhật có chu vi 200 cm. Người ta giảm chiều dài và chiều rộng đi cùng một độ dài thì được một hình chữ nhật mới có chu vi là 160 cm. Hỏi diện tích của phần giảm đi là bao nhiêu?
Câu 5. Cách đây 6 năm, tổng số tuổi của Nam và anh trai Nam là 18 tuổi. Hiện tại, số tuổi của Nam bằng $\frac{2}{3}$ số tuổi của anh trai Nam. Hỏi hiện tại Nam bao nhiêu tuổi?
Câu 6. Vào ngày 18/04/2021, một cửa hàng thịt treo biển khuyến mãi: “Duy nhất ngày hôm nay, thăn bò Úc giảm 40%, chỉ 117000 đồng nửa ký!”. Hỏi, giá thịt thăn bò Úc tại cửa hàng đó trước khi khuyến mãi là bao nhiêu một kg (tính theo đồng)?
Câu 7. Xét biểu thức:
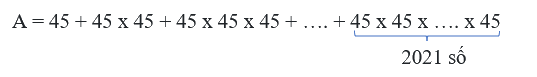
Hỏi khi tính giá trị biểu thức A, giá trị thu được có chữ số hàng đơn vị là bao nhiêu?
Câu 8. Trong dãy 15 ô vuông bên dưới, người ta điền vào mỗi ô vuông một số tự nhiên sao cho tổng các số ở ba ô liên tiếp bất kỳ luôn bằng 39. Tìm số được điền vào ô vuông tô đậm.

Câu 9. Trong hình vẽ dưới, D là điểm trên cạnh AC của tam giác ABC và AD = DC; E là điểm trên đoạn BD thỏa mãn BE : BD = 3 : 5. Biết rằng diện tích tam giác ADE là 96 cm2. Tính diện tích tam giác ABC.
Câu 10. Nam có bốn quyển sách gồm Toán, Tiếng Việt, Tiếng Anh và Lịch Sử. Nam muốn xếp bốn quyển sách này lên một kệ sách trống sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau. Hỏi có bao nhiêu cách xếp?
PHẦN II. TỰ LUẬN
Câu 11. Trong một cuộc thi, có năm thí sinh tham dự là A, B, C, D và E. Trước khi cuộc thi diễn ra, có bốn dự đoán về kết quả xếp hạng của năm thí sinh như sau:
Kết thúc cuộc thi, người ta nhận thấy mỗi người dự đoán đều đúng cho một thí sinh nào đó và sai cho người còn lại. Biết rằng không có hai thí sinh nào có cùng thứ hạng, hỏi ai đứng thứ ba ở cuộc thi đó?
Câu 12. Trong hình vẽ dưới, ABDC và CEFG là hai hình chữ nhật, trong đó điểm B nằm trên cạnh FG của hình chữ nhật CEFG và điểm E nằm trên cạnh AB của hình chữ nhật ABCD thỏa mãn AE : EB = 3 : 2. Biết rằng diện tích hình chữ nhật ABCD là 35 cm2, tính diện tích hình chữ nhật CEFG?
Câu 13. Cho 16 số tự nhiên phân biệt khác 0 thỏa mãn tích của năm số bất kì trong 16 số này là số chẵn. Gọi S là tổng của 16 số này. Biết rằng S là số lẻ, hỏi S có thể nhận giá trị nhỏ nhất là bao nhiêu?
Câu 14. Cho số A = 206920692069…2069 (A gồm 250 số 2069 viết liền nhau). Người ta muốn xóa một số chữ số của số A sao cho số thu được có tổng tất cả các chữ số bằng 2021. Hỏi, có thể xóa được nhiều nhất bao nhiêu chữ số? Khi đó, số lớn nhất có thể thu được là bao nhiêu?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Câu 1. Tính giá trị của biểu thức:
A = 77 x 5,55 + 60,12 x 7,45 + 16,88 x 7,45
Cách giải:
A = 77 x 5,55 + 60,12 x 7,45 + 16,88 x 7,45
A = 77 x 5,55 + 7,45 x (60,12 + 16,88)
A = 77 x 5,55 + 7,45 x 77
A = 77 x (5,55 + 7,45)
A = 77 x 13
A = 1001
Câu 2. Tìm số tự nhiên n biết rằng:
$\left( {1 + \frac{1}{1}} \right) \times \left( {1 + \frac{1}{2}} \right) \times \left( {1 + \frac{1}{3}} \right) \times .... \times \left( {1 + \frac{1}{n}} \right) = 2070$
Cách giải:
$\left( {1 + \frac{1}{1}} \right) \times \left( {1 + \frac{1}{2}} \right) \times \left( {1 + \frac{1}{3}} \right) \times .... \times \left( {1 + \frac{1}{n}} \right) = 2070$
$\frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \times .... \times \frac{{n + 1}}{n} = 2070$
$n + 1 = 2070$
$n = 2069$
Câu 3. Một số tự nhiên được gọi là số tiến nếu các chữ số của nó đôi một khác nhau và chữ số liền sau lớn hơn chữ số liền trước. Ví dụ: 13579 và 24689 là các số tiến; nhưng 11345 không phải là số tiến. Hỏi trong các số tự nhiên từ 2021 đến 2401, có bao nhiêu số là số tiến?
Cách giải:
Các số tiến từ 2021 đến 2401 gồm có 2345 đến 2349 (5 số), 2356 đến 2359 (4 số), 2367, 2368, 2369, 2378, 2379, 2389)
Vậy có 15 số tiến từ 2021 đến 2401.
Câu 4. Một hình chữ nhật có chu vi 200 cm. Người ta giảm chiều dài và chiều rộng đi cùng một độ dài thì được một hình chữ nhật mới có chu vi là 160 cm. Hỏi diện tích của phần giảm đi là bao nhiêu?
Cách giải:
Nửa chu vi ban đầu là: 200 : 2 = 100 (cm) Nửa chu vi lúc sau: 160 : 2 = 80 (cm) Chiều dài và chiều rộng cùng giảm đi: (100 – 80) : 2 = 10 (cm) Phần diện tích giảm đi là: (100 – 10) x 10 = 900 (cm2)
Đáp số: 900cm2
Câu 5. Cách đây 6 năm, tổng số tuổi của Nam và anh trai Nam là 18 tuổi. Hiện tại, số tuổi của Nam bằng $\frac{2}{3}$ số tuổi của anh trai Nam. Hỏi hiện tại Nam bao nhiêu tuổi?
Cách giải:
Tổng số tuổi của Nam và anh trai Nam hiện này là:
18 + 6 + 6 = 30 (tuổi)
Tuổi của Nam hiện nay là:
30 : (2 + 3) x 2 = 12 (tuổi)
Đáp số: 12 tuổi
Câu 6. Vào ngày 18/04/2021, một cửa hàng thịt treo biển khuyến mãi: “Duy nhất ngày hôm nay, thăn bò Úc giảm 40%, chỉ 117000 đồng nửa ký!”. Hỏi, giá thịt thăn bò Úc tại cửa hàng đó trước khi khuyến mãi là bao nhiêu một kg (tính theo đồng)?
Cách giải:
Giá một kg thịt bò sau khi giảm 40% là:
117000 x 2 = 234000 (đồng)
Giá 1 kg thịt thăn bò Úc tại cửa hàng đó trước khi khuyến mãi là:
234000 : 60 x 100 = 390000 (đồng)
Đáp số: 390000 đồng
Câu 7. Xét biểu thức:
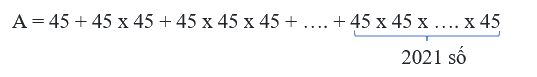
Hỏi khi tính giá trị biểu thức A, giá trị thu được có chữ số hàng đơn vị là bao nhiêu?
Cách giải:
A có 2021 số hạng, mỗi số hạng đều có chữ số hàng đơn vị là 5.
Suy ra A có chữ số hàng đơn vị là hàng đơn vị của tích 5 x 2021.
Vậy A có chữ số tận cùng là 5.
Câu 8. Trong dãy 15 ô vuông bên dưới, người ta điền vào mỗi ô vuông một số tự nhiên sao cho tổng các số ở ba ô liên tiếp bất kỳ luôn bằng 39. Tìm số được điền vào ô vuông tô đậm.

Cách giải:
Ô thứ 3 trong dãy là 11.
Suy ra ô thứ hai trong dãy là: 39 – 20 – 11 = 8
Vì tổng các số ở ba ô liên tiếp bất kỳ luôn bằng 39 nên các số lặp lại theo thứ tự 20, 8, 11.
Vậy số điền vào ô màu xanh là số 8.
Câu 9. Trong hình vẽ dưới, D là điểm trên cạnh AC của tam giác ABC và AD = DC; E là điểm trên đoạn BD thỏa mãn BE : BD = 3 : 5. Biết rằng diện tích tam giác ADE là 96 cm2. Tính diện tích tam giác ABC.
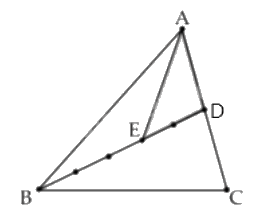
Cách giải:
$\frac{{{S_{ABD}}}}{{{S_{ADE}}}} = \frac{5}{2}$ (Hai tam giác có chung chiều cao hạ từ đỉnh A và đáy $BD = \frac{5}{2}DE$)
Suy ra ${S_{ABD}} = \frac{5}{2} \times {S_{ADE}} = \frac{5}{2} \times 96 = 240$ (cm2)
Ta có ${S_{ABC}} = 2 \times {S_{ABD}}$ (Hai tam giác có chung chiều cao hạ từ B và đáy AC = 2 x AD)
Vậy ${S_{ABC}} = 240 \times 2 = 480$(cm2)
Câu 10. Nam có bốn quyển sách gồm Toán, Tiếng Việt, Tiếng Anh và Lịch Sử. Nam muốn xếp bốn quyển sách này lên một kệ sách trống sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau. Hỏi có bao nhiêu cách xếp?
Cách giải:
Cách cách xếp sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau là:
Toán, Tiếng Việt, Tiếng Anh, Lịch sử
Toán, Tiếng Việt, Lịch sử, Tiếng Anh
Toán, Tiếng Anh, Tiếng Việt, Lịch sử
Toán, Tiếng Anh, Lịch sử, Tiếng Việt
Tiếng Việt, Toán, Tiếng Anh, Lịch sử
Tiếng Việt, Lịch sử, Tiếng Anh, Toán
Tiếng Anh, Toán, Tiếng Việt, Lịch sử
Tiếng Anh, Lịch sử, Tiếng Việt, Toán
Lịch sử, tiếng Anh, Tiếng Việt, Toán
Lịch sử, Tiếng Anh, Toán, Tiếng Việt
Lịch sử, Tiếng Việt, Tiếng Anh, Toán
Lịch sử, Tiếng Việt, Toán, Tiếng Anh
Vậy có 12 cách xếp.
PHẦN II. TỰ LUẬN
Câu 11. Trong một cuộc thi, có năm thí sinh tham dự A, B, C, D và E. Trước khi cuộc thi diễn ra, có bốn dự đoán về kết quả xếp hạng của năm thí sinh như sau:
Kết thúc cuộc thi, người ta nhận thấy mỗi người dự đoán đều đúng cho một thí sinh nào đó và sai cho người còn lại. Biết rằng không có hai thí sinh nào có cùng thứ hạng, hỏi ai đứng thứ ba ở cuộc thi đó?
Cách giải:
Xuất phát từ dự đoán thứ nhất: Nếu B đứng thứ 4 là đúng và E đứng thứ hai là sai, khi đó ở dự đoán thứ 3, E đứng thứ ba sẽ đúng và A đứng thứ 4 sẽ sai. Ở dự đoán thứ tư, A đứng thứ ba sẽ sai và B đứng thứ nhất sẽ đúng (vô lý vì B không thể vừa đứng thứ tư, vừa đứng thứ nhất). Do vậy ở dự đoán thứ nhất, B đứng thứ tư là sai và E đứng thứ hai là đúng. Lúc này ở dự đoán số 3, E đứng thứ ba là sai và A đứng thứ tư đúng. Ở dự đoán thứ tư, A đứng thứ ba sai và B đứng thứ nhất đúng. Ở dự đoán số hai, D đứng nhất sai và C đứng thứ ba đúng. Vậy B đứng thứ nhất, E đứng thứ hai, C đứng thứ ba và A đứng thứ tư.
Câu 12. Trong hình vẽ bên dưới, ABDC và CEFG là hai hình chữ nhật, trong đó điểm B nằm trên cạnh FG của hình chữ nhật CEFG và điểm E nằm trên cạnh AB của hình chữ nhật ABCD thỏa mãn AE : EB = 3 : 2. Biết rằng diện tích hình chữ nhật ABCD là 35 cm2, tính diện tích hình chữ nhật CEFG?
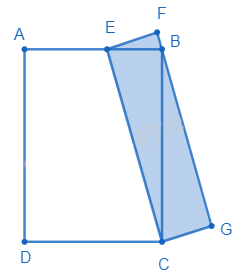
Cách giải:
${S_{ABC}} = \frac{1}{2} \times {S_{ABCD}} = \frac{1}{2} \times 35 = \frac{{35}}{2}$(cm2)
Ta có $\frac{{{S_{EBC}}}}{{{S_{ABC}}}} = \frac{2}{5}$ (Hai tam giác có chung chiều cao hạ từ C và $EB = \frac{2}{5}AB$)
Suy ra ${S_{EBC}} = \frac{2}{5} \times \frac{{35}}{2} = 7$ (cm2)
Ta có $SCEFG = 2 \times {S_{EBC}} = 2 \times 7 = 14$ (cm2)
Đáp số: 14 cm2
Câu 13. Cho 16 số tự nhiên phân biệt khác 0 thỏa mãn tích của năm số bất kì trong 16 số này là số chẵn. Gọi S là tổng của 16 số này. Biết rằng S là số lẻ, hỏi S có thể nhận giá trị nhỏ nhất là bao nhiêu?
Cách giải:
Do tích của 5 số bất kỳ luôn chẵn nên số lượng số lẻ tối đa là 4 số lẻ. Ngoài ra do tổng của 16 số này là lẻ nên chỉ có thể có 1 số lẻ hoặc 3 số lẻ. Nếu có 1 số lẻ thì tổng 16 số nhỏ nhất là 1 + 2 + 4 + 6 + 8 + ... + 30 = 241 Nếu có 3 số lẻ thì tổng 16 số nhỏ nhất là 1 + 3 + 5 + 2 + 4 + 6 + ….. + 26 = 191 Vậy tổng S nhỏ nhất là 191
Câu 14. Cho số A = 206920692069…2069 (A gồm 250 số 2069 viết liền nhau). Người ta muốn xóa một số chữ số của số A sao cho số thu được có tổng tất cả các chữ số bằng 2021. Hỏi, có thể xóa được nhiều nhất bao nhiêu chữ số? Khi đó, số lớn nhất có thể thu được là bao nhiêu?
Cách giải:
A đang có tổng các chữ số là (2 + 0 + 6 + 9) x 250 = 4250 Tổng các chữ số cần xóa đi: 4250 – 2021 = 2229. Trước tiên ta xóa hết 250 chữ số 0. Tiếp theo, nhận thấy 2229 chia hết cho 3, các chữ số 6 và 9 cũng chia hết cho 3 nên số lượng chữ số 2 xóa đi cũng phải chia hết cho 3. Có 250 chữ số 2, vậy ta xóa đi 249 chữ số 2. Lúc này tổng các chữ số 6 và 9 cần xóa là: 2229 – 249 x 2 = 1731. Nhận thấy số lượng chữ số 6 cần xóa phải nhiều nhất có thể, có 250 chữ số 6 nên ta thử:
+) Nếu xóa hết 250 chữ số 6 thì tổng các chữ số 9 cần xóa là 1731 – 250 x 6 = 231 không chia hết cho 9. +) Nếu xóa 249 chữ số 6 thì tổng các chữ số 9 cần xóa là 1731 – 249 x 6 = 237 không chia hết cho 9. +) Nếu xóa 248 chữ số 6 thì tổng các chữ số 9 cần xóa là 1731 – 248 x 6 = 243 chia hết cho 9) cần xóa 243 : 9 = 27 chữ số 9. Vậy cần xóa nhiều nhất 250 chữ số 0; 249 chữ số 2; 248 chữ số 6 và 27 chữ số 9, tức là 250 + 249 + 248 + 27 = 774 chữ số. Lúc này còn lại 226 chữ số gồm 1 chữ số 2; 2 chữ số 6 và 223 chữ số 9. Số lớn nhất có thể thu được là 9999… 9999662.
Kỳ thi tuyển sinh vào lớp 6 trường Archimedes nổi tiếng với độ khó và tính phân loại cao. Để giúp các em học sinh nắm vững kiến thức và tự tin đối mặt với kỳ thi, giaitoan.edu.vn xin giới thiệu chi tiết về bộ đề thi vào lớp 6 môn Toán trường Archimedes năm 2021 (bài nâng cao).
Đề thi vào lớp 6 trường Archimedes năm 2021 (bài nâng cao) thường bao gồm các dạng bài tập sau:
Nội dung đề thi tập trung vào các chủ đề chính sau:
Dưới đây là hướng dẫn giải một số bài tập tiêu biểu trong bộ đề thi vào lớp 6 trường Archimedes năm 2021 (bài nâng cao):
Ví dụ: Tính nhanh giá trị của biểu thức: 123 + 456 + 789
Hướng dẫn: Sử dụng tính chất kết hợp và giao hoán của phép cộng để nhóm các số có tổng tròn chục, tròn trăm, tròn nghìn.
Ví dụ: Một cửa hàng có 350 kg gạo. Buổi sáng bán được 1/5 số gạo, buổi chiều bán được 2/7 số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Hướng dẫn:
Ví dụ: Một hình chữ nhật có chiều dài 12cm, chiều rộng 8cm. Tính diện tích và chu vi của hình chữ nhật đó.
Hướng dẫn:
Ngoài bộ đề thi vào lớp 6 trường Archimedes năm 2021 (bài nâng cao), các em học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Giaitoan.edu.vn hy vọng với những thông tin chi tiết và hướng dẫn giải trên, các em học sinh sẽ tự tin hơn khi bước vào kỳ thi tuyển sinh vào lớp 6 trường Archimedes. Chúc các em thành công!