Giaitoan.edu.vn cung cấp bộ đề thi thử vào lớp 6 môn Toán trường Cầu Giấy năm 2024 được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
Đây là tài liệu ôn tập vô cùng hữu ích giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi quan trọng.
Chúng tôi luôn cập nhật những đề thi mới nhất và chất lượng nhất để hỗ trợ học sinh đạt kết quả tốt nhất.
Một người đi xe máy qua 1 cây cầu dài 1 875 m hết 3 phút Quãng đường AB có độ dài 95kmĐể hưởng ứng ngày hội sách bạn Liên đã tham gia đọc 1 cuốn sách dày 375 trang trong 4 ngày
PHẦN 1. TRẮC NGHIỆM
Bài 1. Hỗn số \(2\frac{3}{4}\) được viết dưới dạng số thập phân là:
A. 2,075 B. 2,34 C. 2,75 D. 27,5
Bài 2. Đổi 2 ha 15 m2 =.... ha.
A. 2,0015 B. 2,15 C. 2,015 D. 20 015
Bài 3. Một người đi xe máy qua 1 cây cầu dài 1 875 m hết 3 phút. Hỏi 1 giờ người đó đi được quãng đường dài bao nhiêu?
A. 625 m B. 37,5 km C. 33,75 km D. 93, 75 km
Bài 4. Một hình hộp chữ nhật có chu vi là 36 cm. Chiều rộng bằng 8 cm. Chiều cao bằng $\frac{3}{4}$ chiều rộng. Tính thể tích hình này.
A. 168 cm3 B. 216 cm3 C. 285 cm3 D. 480 cm3
Bài 5. Có 1 500 du khách được hỏi về món ăn yêu thích nhất ở VN thì có 25% số người thích ăn bánh chả, 18% thích ăn bánh mỳ và 43% thích ăn phở, còn lại thích ăn bánh cuốn. Tìm số người thích ăn bánh cuốn.
Bài 6. Quãng đường AB có độ dài 95km. Lúc 6 giờ một ô tô đi từ A với vận tốc 50 km/giờ sau 30 phút ô tô giảm vận tốc còn 40 km/ giờ. Hỏi ô tô đến B lúc mấy giờ?
Bài 7. Hiện nay tổng tuổi của bố và con là 50 tuổi. Ba năm trước, tuổi bố gấp 4,5 lần tuổi con. Tính tuổi bố hiện nay.
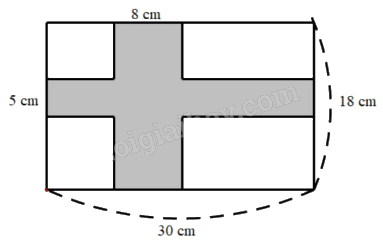
Bài 8. Tính diện tích phân tô đậm.
PHẦN 2. TỰ LUẬN
Bài 9. Để hưởng ứng ngày hội sách bạn Liên đã tham gia đọc 1 cuốn sách dày 375 trang trong 4 ngày. Ngày 1 bạn ấy đọc được số trang bằng với $\frac{1}{5}$ tổng số trang của quyển sách. Ngày 2 đọc được số trang bằng với $\frac{5}{6}$ số trang mà ngày 3 đọc được.
Số trang mà ngày 3 đọc được gấp 1,5 lần số trang mà ngày 4 đọc được
a) Tìm số trang ngày 1 đã đọc
b) Tìm số trang ngày 4 Liên đã đọc
Bài 10. Cho hai số tự nhiên a và b (a < b) biết (a x b) x (a + b) = 30.
a) Tìm các số a và b thỏa mãn điều kiện trên.
b) Có thể tìm được 2 số tự nhiên a và b để a x b x (a + b) = 20242025 hay không? Vì sao?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Câu 1. Hỗn số \(2\frac{3}{4}\) được viết dưới dạng số thập phân là:
A. 2,075 B. 2,34 C. 2,75 D. 27,5
Lời giải
$2\frac{3}{4} = 2\frac{{75}}{{100}} = 2,75$
Đáp án: C
Câu 2. Đổi 2 ha 15 m2 =.... ha.
A. 2,0015 B. 2,15 C. 2,015 D. 20 015
Lời giải
2 ha 15 m2 = $2\frac{{15}}{{10000}} = 2,0015$ ha
Đáp án: A
Bài 3. Một người đi xe máy qua 1 cây cầu dài 1 875 m hết 3 phút. Hỏi 1 giờ người đó đi được quãng đường dài bao nhiêu?
A. 625 m B. 37,5 km C. 33,75 km D. 93, 75 km
Lời giải
1 giờ = 60 phút.
60 phút gấp 3 phút số lần là:
60 : 3 = 20 (lần)
1 giờ người đó đi được quãng đường dài là:
1 875 x 20 = 37 500 (m) = 37,5 km
Đáp án: B
Bài 4. Một hình hộp chữ nhật có chu vi là 36 cm. Chiều rộng bằng 8 cm. Chiều cao bằng $\frac{3}{4}$ chiều rộng. Tính thể tích hình này.
A. 168 cm3 B. 216 cm3 C. 285 cm3 D. 480 cm3
Lời giải
Tổng chiều dài và chiều rộng là: 36 : 2 = 18 (cm)
Chiều dài có độ dài là: 18 - 8 = 10 (cm)
Chiều cao của hình hộp chữ nhật là: $8 \times \frac{3}{4} = 6$ (cm)
Thể tích của hình hộp chữ nhật này là: 10 x 8 x 6 = 480 (cm3)
Đáp án: D
Bài 5. Có 1 500 du khách được hỏi về món ăn yêu thích nhất ở VN thì có 25% số người thích ăn bánh chả, 18% thích ăn bánh mỳ và 43% thích ăn phở, còn lại thích ăn bánh cuốn. Tìm số người thích ăn bánh cuốn.
Lời giải
Tỉ số phần trăm người ăn bánh cuốn so với số du khách là:
100% - (25% + 18% + 43%) = 14%
Số người thích ăn bánh cuốn là:
1 500 x 14% = 210 (người)
Đáp án: 210 người
Bài 6. Quãng đường AB có độ dài 95km. Lúc 6 giờ một ô tô đi từ A với vận tốc 50 km/giờ sau 30 phút ô tô giảm vận tốc còn 40 km/ giờ. Hỏi ô tô đến B lúc mấy giờ?
Lời giải
Đổi: 30 phút = $\frac{1}{2}$ giờ
Sau 30 phút ô tô đã đi được quãng đường là:
$50 \times \frac{1}{2} = 25$ (km)
Quãng đường ô tô còn phải đi là:
95 - 25 = 70 (km)
Thời gian ô tô cần phải đi với vận tốc 40 km/ giờ là:
$70:40 = \frac{7}{4} = 1,75$ (giờ) = 1 giờ 45 phút
Ô tô đến B lúc: 6 giờ + 30 phút + 1 giờ 45 phút = 8 giờ 15 phút.
Đáp án: 8 giờ 15 phút
Bài 7. Hiện nay tổng tuổi của bố và con là 50 tuổi. Ba năm trước, tuổi bố gấp 4,5 lần tuổi con. Tính tuổi bố hiện nay.
Lời giải
Tổng tuổi hai bố con 3 năm trước là:
50 – 3 x 2 = 44 (tuổi)
Tuổi bố 3 năm trước là:
44 : (4,5 + 1) x 4,5 = 36 (tuổi)
Tuổi bố hiện nay là:
36 + 3 = 39 (tuổi)
Đáp án: 39 tuổi
Bài 8. Tính diện tích phân tô đậm.
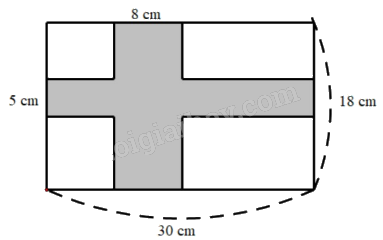
Lời giải
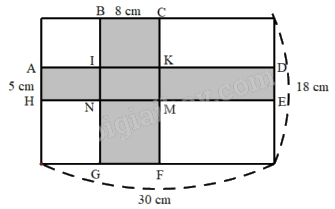
Diện tích hình chữ nhật ADEH là: 5 x 30 = 150 (cm2)
Diện tích hình chữ nhật BCFG là: 8 x 18 = 144 (cm2)
Diện tích hình chữ nhật IKMN là: 8 x 5 = 40 (cm2)
Diện tích phần tô đậm là: 150 + 144 - 40 = 254 (cm2)
Đáp án: 254 cm2
PHẦN 2. TỰ LUẬN
Bài 9. Để hưởng ứng ngày hội sách bạn Liên đã tham gia đọc 1 cuốn sách dày 375 trang trong 4 ngày. Ngày 1 bạn ấy đọc được số trang bằng với $\frac{1}{5}$ tổng số trang của quyển sách. Ngày 2 đọc được số trang bằng với $\frac{5}{6}$ số trang mà ngày 3 đọc được.
Số trang mà ngày 3 đọc được gấp 1,5 lần số trang mà ngày 4 đọc được
a) Tìm số trang ngày 1 đã đọc.
b) Tìm số trang ngày 4 Liên đã đọc.
Lời giải
a) Số trang sách ngày thứ nhất bạn Liên đã đọc được là:
$375 \times \frac{1}{5} = 75$ (trang)
b) Sau ngày thứ nhất, bạn Liên còn phải đọc số trang sách là:
375 - 75 = 300 (trang)
Ngày thứ hai bạn Liên đọc được số phần trang sách so với ngày thứ tư là:
$\frac{5}{6} \times 1,5 = \frac{5}{4}$ (ngày thứ tư)
Ngày thứ ba bạn Liên đọc được số phần trang sách so với ngày thứ tư là: 1,5 = $\frac{3}{2}$
3 ngày còn lại bạn Liên đọc được số phần trang sách so với ngày thứ tư là:
$\frac{5}{4} + \frac{3}{2} + 1 = \frac{{15}}{4}$ (ngày thứ tư)
Số trang ngày thứ tư bạn Liên đã đọc là:
$300:\frac{{15}}{4} = 80$ (trang)
Đáp số: a) 75 trang
b) 80 trang
Bài 10. Cho hai số tự nhiên a và b (a < b) biết (a x b) x (a + b) = 30.
a) Tìm các số a và b thỏa mãn điều kiện trên.
b) Có thể tìm được 2 số tự nhiên a và b để a x b x (a + b) = 20242025 hay không? Vì sao?
Lời giải
a) Cách 1: 30 = 1 x 2 x 15 = 1 x 3 x 10 = 1 x 5 x 6 = 2 x 3 x 5
Từ đây ta thấy có 2 trường hợp thỏa mãn a và b sao cho a < b là:
Trường hợp 1: a x b x (a + b) = 1 x 5 x 6 nên a = 1 và b = 5
Trường hợp 2: a x b x (a + b) = 2 x 3 x 5 nên a = 2 và b = 3
b) Xét trường hợp a và b là số lẻ ta có:
(a x b) là số lẻ vì số lẻ nhân với số lẻ được tích là số lẻ.
(a + b) là số chẵn vì số lẻ cộng với số lẻ được tổng là số chẵn.
Ta có: (a x b) x (a + b) = số lẻ x số chẵn = số chẵn. Mà 20242025 là số lẻ nên a và b không thể là số lẻ.
Xét trường hợp a và b đều là số chẵn ta có:
(a x b) là số chẵn vì số chẵn nhân với số chẵn được tích là số chẵn.
(a + b) là số chẵn vì số chẵn cộng với số chẵn được tổng là số chẵn.
Ta có: (a x b) x (a + b) = số chẵn x số chẵn = số chẵn. Mà 20242025 là số lẻ nên a và b không thể là số chẵn.
Xét trường hợp a và b có 1 số chẵn và 1 số lẻ, ta có:
(a x b) là số chẵn vì số chẵn nhân với số lẻ được tích là số chẵn
(a + b) là số lẻ vì số lẻ cộng với số chẵn được tổng là số lẻ.
Ta có: (a x b) x (a + b) = số chẵn x số lẻ. Mà 20242025 là số lẻ nên a và b không thể có 1 số lẻ và một số chẵn.
Vậy không thể tìm được 2 số tự nhiên a và b thỏa mãn a x b x (a + b) = 20242025.
Đáp số: a) a = 1 và b = 5 hoặc a = 2 và b = 3;
b) Không thể tìm được hai số a và b thỏa mãn đề bài.
PHẦN 1. TRẮC NGHIỆM
Bài 1. Hỗn số \(2\frac{3}{4}\) được viết dưới dạng số thập phân là:
A. 2,075 B. 2,34 C. 2,75 D. 27,5
Bài 2. Đổi 2 ha 15 m2 =.... ha.
A. 2,0015 B. 2,15 C. 2,015 D. 20 015
Bài 3. Một người đi xe máy qua 1 cây cầu dài 1 875 m hết 3 phút. Hỏi 1 giờ người đó đi được quãng đường dài bao nhiêu?
A. 625 m B. 37,5 km C. 33,75 km D. 93, 75 km
Bài 4. Một hình hộp chữ nhật có chu vi là 36 cm. Chiều rộng bằng 8 cm. Chiều cao bằng $\frac{3}{4}$ chiều rộng. Tính thể tích hình này.
A. 168 cm3 B. 216 cm3 C. 285 cm3 D. 480 cm3
Bài 5. Có 1 500 du khách được hỏi về món ăn yêu thích nhất ở VN thì có 25% số người thích ăn bánh chả, 18% thích ăn bánh mỳ và 43% thích ăn phở, còn lại thích ăn bánh cuốn. Tìm số người thích ăn bánh cuốn.
Bài 6. Quãng đường AB có độ dài 95km. Lúc 6 giờ một ô tô đi từ A với vận tốc 50 km/giờ sau 30 phút ô tô giảm vận tốc còn 40 km/ giờ. Hỏi ô tô đến B lúc mấy giờ?
Bài 7. Hiện nay tổng tuổi của bố và con là 50 tuổi. Ba năm trước, tuổi bố gấp 4,5 lần tuổi con. Tính tuổi bố hiện nay.
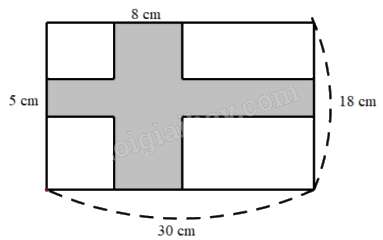
Bài 8. Tính diện tích phân tô đậm.
PHẦN 2. TỰ LUẬN
Bài 9. Để hưởng ứng ngày hội sách bạn Liên đã tham gia đọc 1 cuốn sách dày 375 trang trong 4 ngày. Ngày 1 bạn ấy đọc được số trang bằng với $\frac{1}{5}$ tổng số trang của quyển sách. Ngày 2 đọc được số trang bằng với $\frac{5}{6}$ số trang mà ngày 3 đọc được.
Số trang mà ngày 3 đọc được gấp 1,5 lần số trang mà ngày 4 đọc được
a) Tìm số trang ngày 1 đã đọc
b) Tìm số trang ngày 4 Liên đã đọc
Bài 10. Cho hai số tự nhiên a và b (a < b) biết (a x b) x (a + b) = 30.
a) Tìm các số a và b thỏa mãn điều kiện trên.
b) Có thể tìm được 2 số tự nhiên a và b để a x b x (a + b) = 20242025 hay không? Vì sao?
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Câu 1. Hỗn số \(2\frac{3}{4}\) được viết dưới dạng số thập phân là:
A. 2,075 B. 2,34 C. 2,75 D. 27,5
Lời giải
$2\frac{3}{4} = 2\frac{{75}}{{100}} = 2,75$
Đáp án: C
Câu 2. Đổi 2 ha 15 m2 =.... ha.
A. 2,0015 B. 2,15 C. 2,015 D. 20 015
Lời giải
2 ha 15 m2 = $2\frac{{15}}{{10000}} = 2,0015$ ha
Đáp án: A
Bài 3. Một người đi xe máy qua 1 cây cầu dài 1 875 m hết 3 phút. Hỏi 1 giờ người đó đi được quãng đường dài bao nhiêu?
A. 625 m B. 37,5 km C. 33,75 km D. 93, 75 km
Lời giải
1 giờ = 60 phút.
60 phút gấp 3 phút số lần là:
60 : 3 = 20 (lần)
1 giờ người đó đi được quãng đường dài là:
1 875 x 20 = 37 500 (m) = 37,5 km
Đáp án: B
Bài 4. Một hình hộp chữ nhật có chu vi là 36 cm. Chiều rộng bằng 8 cm. Chiều cao bằng $\frac{3}{4}$ chiều rộng. Tính thể tích hình này.
A. 168 cm3 B. 216 cm3 C. 285 cm3 D. 480 cm3
Lời giải
Tổng chiều dài và chiều rộng là: 36 : 2 = 18 (cm)
Chiều dài có độ dài là: 18 - 8 = 10 (cm)
Chiều cao của hình hộp chữ nhật là: $8 \times \frac{3}{4} = 6$ (cm)
Thể tích của hình hộp chữ nhật này là: 10 x 8 x 6 = 480 (cm3)
Đáp án: D
Bài 5. Có 1 500 du khách được hỏi về món ăn yêu thích nhất ở VN thì có 25% số người thích ăn bánh chả, 18% thích ăn bánh mỳ và 43% thích ăn phở, còn lại thích ăn bánh cuốn. Tìm số người thích ăn bánh cuốn.
Lời giải
Tỉ số phần trăm người ăn bánh cuốn so với số du khách là:
100% - (25% + 18% + 43%) = 14%
Số người thích ăn bánh cuốn là:
1 500 x 14% = 210 (người)
Đáp án: 210 người
Bài 6. Quãng đường AB có độ dài 95km. Lúc 6 giờ một ô tô đi từ A với vận tốc 50 km/giờ sau 30 phút ô tô giảm vận tốc còn 40 km/ giờ. Hỏi ô tô đến B lúc mấy giờ?
Lời giải
Đổi: 30 phút = $\frac{1}{2}$ giờ
Sau 30 phút ô tô đã đi được quãng đường là:
$50 \times \frac{1}{2} = 25$ (km)
Quãng đường ô tô còn phải đi là:
95 - 25 = 70 (km)
Thời gian ô tô cần phải đi với vận tốc 40 km/ giờ là:
$70:40 = \frac{7}{4} = 1,75$ (giờ) = 1 giờ 45 phút
Ô tô đến B lúc: 6 giờ + 30 phút + 1 giờ 45 phút = 8 giờ 15 phút.
Đáp án: 8 giờ 15 phút
Bài 7. Hiện nay tổng tuổi của bố và con là 50 tuổi. Ba năm trước, tuổi bố gấp 4,5 lần tuổi con. Tính tuổi bố hiện nay.
Lời giải
Tổng tuổi hai bố con 3 năm trước là:
50 – 3 x 2 = 44 (tuổi)
Tuổi bố 3 năm trước là:
44 : (4,5 + 1) x 4,5 = 36 (tuổi)
Tuổi bố hiện nay là:
36 + 3 = 39 (tuổi)
Đáp án: 39 tuổi
Bài 8. Tính diện tích phân tô đậm.
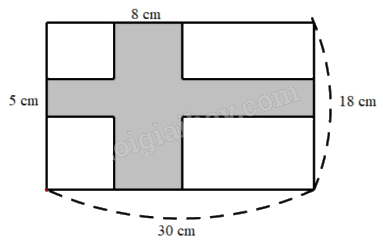
Lời giải
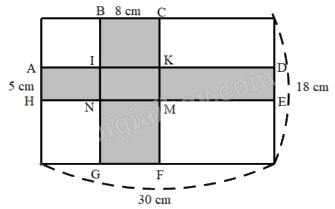
Diện tích hình chữ nhật ADEH là: 5 x 30 = 150 (cm2)
Diện tích hình chữ nhật BCFG là: 8 x 18 = 144 (cm2)
Diện tích hình chữ nhật IKMN là: 8 x 5 = 40 (cm2)
Diện tích phần tô đậm là: 150 + 144 - 40 = 254 (cm2)
Đáp án: 254 cm2
PHẦN 2. TỰ LUẬN
Bài 9. Để hưởng ứng ngày hội sách bạn Liên đã tham gia đọc 1 cuốn sách dày 375 trang trong 4 ngày. Ngày 1 bạn ấy đọc được số trang bằng với $\frac{1}{5}$ tổng số trang của quyển sách. Ngày 2 đọc được số trang bằng với $\frac{5}{6}$ số trang mà ngày 3 đọc được.
Số trang mà ngày 3 đọc được gấp 1,5 lần số trang mà ngày 4 đọc được
a) Tìm số trang ngày 1 đã đọc.
b) Tìm số trang ngày 4 Liên đã đọc.
Lời giải
a) Số trang sách ngày thứ nhất bạn Liên đã đọc được là:
$375 \times \frac{1}{5} = 75$ (trang)
b) Sau ngày thứ nhất, bạn Liên còn phải đọc số trang sách là:
375 - 75 = 300 (trang)
Ngày thứ hai bạn Liên đọc được số phần trang sách so với ngày thứ tư là:
$\frac{5}{6} \times 1,5 = \frac{5}{4}$ (ngày thứ tư)
Ngày thứ ba bạn Liên đọc được số phần trang sách so với ngày thứ tư là: 1,5 = $\frac{3}{2}$
3 ngày còn lại bạn Liên đọc được số phần trang sách so với ngày thứ tư là:
$\frac{5}{4} + \frac{3}{2} + 1 = \frac{{15}}{4}$ (ngày thứ tư)
Số trang ngày thứ tư bạn Liên đã đọc là:
$300:\frac{{15}}{4} = 80$ (trang)
Đáp số: a) 75 trang
b) 80 trang
Bài 10. Cho hai số tự nhiên a và b (a < b) biết (a x b) x (a + b) = 30.
a) Tìm các số a và b thỏa mãn điều kiện trên.
b) Có thể tìm được 2 số tự nhiên a và b để a x b x (a + b) = 20242025 hay không? Vì sao?
Lời giải
a) Cách 1: 30 = 1 x 2 x 15 = 1 x 3 x 10 = 1 x 5 x 6 = 2 x 3 x 5
Từ đây ta thấy có 2 trường hợp thỏa mãn a và b sao cho a < b là:
Trường hợp 1: a x b x (a + b) = 1 x 5 x 6 nên a = 1 và b = 5
Trường hợp 2: a x b x (a + b) = 2 x 3 x 5 nên a = 2 và b = 3
b) Xét trường hợp a và b là số lẻ ta có:
(a x b) là số lẻ vì số lẻ nhân với số lẻ được tích là số lẻ.
(a + b) là số chẵn vì số lẻ cộng với số lẻ được tổng là số chẵn.
Ta có: (a x b) x (a + b) = số lẻ x số chẵn = số chẵn. Mà 20242025 là số lẻ nên a và b không thể là số lẻ.
Xét trường hợp a và b đều là số chẵn ta có:
(a x b) là số chẵn vì số chẵn nhân với số chẵn được tích là số chẵn.
(a + b) là số chẵn vì số chẵn cộng với số chẵn được tổng là số chẵn.
Ta có: (a x b) x (a + b) = số chẵn x số chẵn = số chẵn. Mà 20242025 là số lẻ nên a và b không thể là số chẵn.
Xét trường hợp a và b có 1 số chẵn và 1 số lẻ, ta có:
(a x b) là số chẵn vì số chẵn nhân với số lẻ được tích là số chẵn
(a + b) là số lẻ vì số lẻ cộng với số chẵn được tổng là số lẻ.
Ta có: (a x b) x (a + b) = số chẵn x số lẻ. Mà 20242025 là số lẻ nên a và b không thể có 1 số lẻ và một số chẵn.
Vậy không thể tìm được 2 số tự nhiên a và b thỏa mãn a x b x (a + b) = 20242025.
Đáp số: a) a = 1 và b = 5 hoặc a = 2 và b = 3;
b) Không thể tìm được hai số a và b thỏa mãn đề bài.
Kỳ thi vào lớp 6 môn Toán trường Cầu Giấy là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc luyện tập với các đề thi thử và nắm vững kiến thức là vô cùng cần thiết. Bài viết này sẽ cung cấp cho bạn những thông tin chi tiết về đề thi vào lớp 6 môn Toán trường Cầu Giấy năm 2024, cùng với các lời khuyên hữu ích để đạt kết quả cao nhất.
Đề thi vào lớp 6 môn Toán trường Cầu Giấy thường bao gồm các dạng bài tập sau:
Tỷ lệ phân bổ điểm giữa các dạng bài tập có thể thay đổi tùy theo từng năm, nhưng thường tập trung vào các chủ đề chính như:
Để giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán, Giaitoan.edu.vn cung cấp bộ đề thi thử vào lớp 6 môn Toán trường Cầu Giấy năm 2024. Các đề thi này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với trình độ của học sinh.
Dưới đây là một số đề thi thử mà bạn có thể tham khảo:
Để đạt kết quả tốt nhất trong kỳ thi vào lớp 6 môn Toán trường Cầu Giấy, bạn nên:
Ngoài các đề thi thử, bạn có thể tham khảo thêm các tài liệu ôn tập hữu ích sau:
Dưới đây là phân tích chi tiết một số dạng bài tập thường gặp trong đề thi vào lớp 6 môn Toán trường Cầu Giấy:
Các bài tập tính nhanh thường yêu cầu học sinh vận dụng các tính chất của phép toán để rút gọn biểu thức và tìm ra kết quả nhanh nhất. Ví dụ:
Tính: 123 + 456 + 789
Lời giải: (123 + 789) + 456 = 912 + 456 = 1368
Các bài tập giải toán có lời văn đòi hỏi học sinh phải đọc kỹ đề bài, xác định đúng các yếu tố đã cho và yêu cầu tìm, sau đó lập luận và giải bài toán một cách logic. Ví dụ:
Một người có 36 quả cam. Người đó chia đều số cam cho 4 bạn. Hỏi mỗi bạn được chia bao nhiêu quả cam?
Lời giải: Số cam mỗi bạn được chia là: 36 : 4 = 9 (quả)
Các bài toán về tỷ số yêu cầu học sinh hiểu và vận dụng các khái niệm về tỷ số, tỷ lệ để giải quyết bài toán. Ví dụ:
Tỉ số giữa số học sinh nam và số học sinh nữ của một lớp là 3:2. Biết lớp đó có 30 học sinh. Hỏi lớp đó có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?
Lời giải: Tổng số phần bằng nhau là: 3 + 2 = 5 (phần)
Số học sinh nam là: 30 : 5 x 3 = 18 (học sinh)
Số học sinh nữ là: 30 : 5 x 2 = 12 (học sinh)
Hy vọng với những thông tin và lời khuyên trên, bạn sẽ tự tin hơn trong kỳ thi vào lớp 6 môn Toán trường Cầu Giấy năm 2024. Chúc bạn thành công!