Giaitoan.edu.vn xin giới thiệu bộ đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ, được thiết kế để giúp các em học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán. Đề số 2 này tập trung vào các dạng bài tập thường gặp trong kỳ thi tuyển sinh, giúp các em tự tin hơn khi bước vào phòng thi.
Đề thi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, có đáp án chi tiết và lời giải dễ hiểu. Các em có thể sử dụng đề thi này để tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Hiện nay, ông hơn cháu 66 tuổi. Sang năm, tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm. Dũng sinh vào tháng 4. Năm 2020, sinh nhật Dũng vào ngày Chủ nhật.
ĐỀ THI THỬ VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM 2024
MÔN: TOÁN
Đề số 2
Nguồn: Sưu tầm
I. TRẮC NGHIỆM
Câu 1. Hiện nay, ông hơn cháu 66 tuổi. Sang năm, tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm. Tuổi cháu hiện nay là:
A. 4 tuổi B. 5 tuổi C. 6 tuổi D. 7 tuổi
Câu 2. Một số có ba chữ số có tích các chữ số là 7. Tổng các chữ số của số đó là
A. 9 B. 8 C. 7 D. 6
Câu 3. Dũng sinh vào tháng 4. Năm 2020, sinh nhật Dũng vào ngày Chủ nhật. Năm 2024 sinh nhật Dũng vào thứ mấy?
A. Thứ năm B. Thứ sáu C. Thứ bảy D. Chủ nhật
Câu 4. Một tấm bìa hình chữ nhật có chu vi bằng 68cm, chiều dài bằng $\frac{{12}}{5}$ chiều rộng. Diện tích tấm bìa này bằng $\frac{2}{3}$ diện tích tấm bìa hình tam giác. Biết chiều cao tấm bìa hình tam giác là 18 cm, độ dài cạnh đáy tương ứng bằng:
A. 10 cm B. 20 cm C. 40 cm D. 80 cm
Câu 5. Hàng ngày, An đi từ nhà lúc 7 giờ 25 phút và tới trường lúc 8 giờ kém 20 phút. Sáng nay do ngủ dậy muộn nên 7 giờ rưỡi An mới xuất phát. An tính rằng để đến trường đúng giờ, mỗi phút bạn phải đi nhanh hơn hàng ngày 50m. Độ dài quãng đường từ nhà An đến trường là:
A. 2,5 cm B. 2 km C. 1,5 km D. 1 km
II. TỰ LUẬN
Câu 1. Đầu năm học, bốn bạn An, Toàn, Giao, Thông mua một số quyền vờ. Số vở của An bằng $\frac{1}{2}$ tổng số vở của ba bạn còn lại. Số vở của Toàn bằng $\frac{1}{5}$ tổng số vở của ba bạn còn lại. Số vở của Giao bằng $\frac{3}{2}$ số vở của Thông. Tính số vở của mỗi bạn, biết An có nhiều hơn toàn 10 quyển vở.
Câu 2. Cho hình thang vuông ABCD có góc B và góc C vuông, đáy nhỏ AB bằng $\frac{2}{5}$ đáy lớn CD, kẻ chiều cao AH.
a) Tính tỉ số của diện tích hình chữ nhật ABCH và diện tích tam giác AHD.
b) Lấy M trên AH sao cho $MH = \frac{1}{3}AH$, kéo dài CM cắt AD tại N. Tính tỉ số của AN và ND.
HƯỚNG DẪN GIẢI CHI TIẾT
I. TRẮC NGHIỆM
Câu 1. Hiện nay, ông hơn cháu 66 tuổi. Sang năm, tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm. Tuổi cháu hiện nay là:
A. 4 tuổi B. 5 tuổi C. 6 tuổi D. 7 tuổi
Lời giải
Vì năm sau, tuổi cháu có bao nhiêu tháng thì tuổi ông là bấy nhiêu năm, mà mỗi năm có 12 tháng, nên năm sau tuổi ông gấp 12 lần tuổi cháu.
Ông hơn cháu 66 tuổi nên tuổi cháu năm sau là: 66 : (12 -1) ´1 = 6 (tuổi)
Tuổi cháu hiện nay là: 6 – 1 = 5 (tuổi)
Đáp án: B
Câu 2. Một số có ba chữ số có tích các chữ số là 7. Tổng các chữ số của số đó là
A. 9 B. 8 C. 7 D. 6
Lời giải:
Ta có: 7 = 7 x 1 x 1
Vì tích các chữ số của số đó là 7 nên số đó là 117 hoặc 171 hoặc 711. Tổng các chữ số của số đó là:
1 + 1 + 7 = 9
Đáp án: A
Câu 3. Dũng sinh vào tháng 4. Năm 2020, sinh nhật Dũng vào ngày Chủ nhật. Năm 2024 sinh nhật Dũng vào thứ mấy?
A. Thứ năm B. Thứ sáu C. Thứ bảy D. Chủ nhật
Lời giải:
Mỗi năm có 365 ngày, nhưng năm 2024 là năm nhuận nên sẽ có ngày 29 tháng 2.
Số ngày từ sinh nhật năm 2020 đến sinh nhật năm 2024 của Dũng là: 365´ 4 + 1 = 1461 (ngày)
Ta có 1461 : 7 = 208 (dư 5)
Ta thấy, số ngày chia chia hết cho 7 là chủ nhật nên số ngày chia 7 dư 5 là thứ sáu. Vậy sinh nhật Dũng năm 2024 là Thứ Sáu.
Đáp án: B
Câu 4. Một tấm bìa hình chữ nhật có chu vi bằng 68cm, chiều dài bằng $\frac{{12}}{5}$ chiều rộng. Diện tích tấm bìa này bằng $\frac{2}{3}$ diện tích tấm bìa hình tam giác. Biết chiều cao tấm bìa hình tam giác là 18 cm, độ dài cạnh đáy tương ứng bằng:
A. 10 cm B. 20 cm C. 40 cm D. 80 cm
Lời giải
Nửa chu vi hình chữ nhật là 68 : 2 = 34 (cm)
Chiều dài hình chữ nhật là 34 : (12 + 5) x 12 = 24 (cm)
Chiều dài hình chữ nhật là 34 – 24 = 10 (cm)
Diện tích tấm bìa hình chữ nhật là 24 x 10 = 240 (cm2)
Diện tích tấm bìa hình tam giác là:
$240:\frac{2}{3} = 360$ (cm2)
Độ dài cạnh đáy tương ứng bằng: 360 x 2 : 18 = 40 (cm)
Đáp án: C
Câu 5. Hàng ngày, An đi từ nhà lúc 7 giờ 25 phút và tới trường lúc 8 giờ kém 20 phút. Sáng nay do ngủ dậy muộn nên 7 giờ rưỡi An mới xuất phát. An tính rằng để đến trường đúng giờ, mỗi phút bạn phải đi nhanh hơn hàng ngày 50m. Độ dài quãng đường từ nhà An đến trường là:
A. 2,5 cm B. 2 km C. 1,5 km D. 1 km
Lời giải
Đổi: 8 giờ kém 20 phút = 7 giờ 40 phút
Thời gian An đi từ nhà đến trường là 7 giờ 40 phút – 7 giờ 25 phút = 15 phút
Thời gian bạn An phải đi hôm nay là: 7 giờ 40 phút – 7 giờ 30 phút = 10 phút
Trên cùng quãng đường AB thì thời gian và vận tốc là hai đại lượng tỉ lệ nghịch.
Tỉ số thời gian An đi hôm nay và mọi ngày An đi là: $\frac{{10}}{{15}} = \frac{2}{3}$
Tỉ số vận tốc của An hôm nay và mọi ngày là: $\frac{3}{2}$
Vận tốc của An hôm nay là: 50 : (3 - 2) ´ 3 = 150 (m/phút)
Quảng đường từ nhà đến trường là: 150´10 =1500 (m) = 1,5 km
Đáp án: C
II. TỰ LUẬN
Câu 1. Đầu năm học, bốn bạn An, Toàn, Giao, Thông mua một số quyển vở. Số vở của An bằng $\frac{1}{2}$ tổng số vở của ba bạn còn lại. Số vở của Toàn bằng $\frac{1}{5}$ tổng số vở của ba bạn còn lại. Số vở của Giao bằng $\frac{3}{2}$ số vở của Thông. Tính số vở của mỗi bạn, biết An có nhiều hơn Toàn 10 quyển vở.
Cách giải:
Số vở của An bằng $\frac{1}{2}$ tổng số vở của ba bạn còn lại nên số vở của An bằng $\frac{1}{3}$ tổng số vở.
Số vở của Toàn bằng $\frac{1}{5}$ tổng số vở của ba bạn còn lại nên số vở của Toàn bằng $\frac{1}{6}$ tổng số vở.
Biết An có nhiều hơn Toàn 10 quyển vở.
10 quyển vở ứng với phân số $\frac{1}{3} - \frac{1}{6} = \frac{1}{6}$ (tổng số vở)
Tổng số vở của 4 bạn là: $10:\frac{1}{6} = 60$(quyển vở)
Số vở của An là $60 \times \frac{1}{3} = 20$ (quyển)
Số vở của Toàn là 20 – 10 = 10 (quyển)
Số vở của Giao và Thông là 60 – 20 – 10 = 30 (quyển)
Ta có: Số vở của Giao bằng $\frac{3}{2}$ số vở của Thông.
Số vở của Giao là 30 : (3 + 2) x 3 = 18 (quyển)
Số vở của Thông là 30 – 18 = 12 (quyển)
Đáp số: An: 20 quyển
Toàn: 10 quyển
Giao: 18 quyển
Thông: 12 quyển
Câu 2. Cho hình thang vuông ABCD có góc B và góc C vuông, đáy nhỏ AB bằng $\frac{2}{5}$ đáy lớn CD, kẻ chiều cao AH.
a) Tính tỉ số của diện tích hình chữ nhật ABCH và diện tích tam giác AHD.
b) Lấy M trên AH sao cho $MH = \frac{1}{3}AH$, kéo dài CM cắt AD tại N. Tính tỉ số của AN và ND.
Lời giải
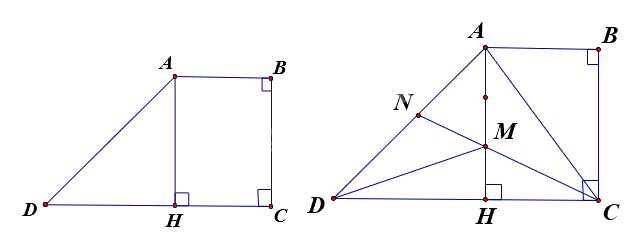
a) Ta có ${S_{ABCH}} = AB \times AH$ và ${S_{AHD}} = \frac{{AH \times HD}}{2}$
Mà $AB = \frac{2}{5}CD$ nên $AB = \frac{2}{3}HD$
Suy ra ${S_{ABCH}} = \frac{2}{3}HD \times AH = \frac{{2 \times HD \times AH}}{3}$. Từ đó suy ra $\frac{{{S_{ABCH}}}}{{{S_{AHD}}}} = \frac{4}{3}$
b) Ta có $\frac{{SCMA}}{{SCMH}} = \frac{{MA}}{{MH}} = \frac{2}{1} = \frac{4}{2}$ (chung chiều cao hạ từ C xuống AH)
$\frac{{{S_{CMH}}}}{{{S_{CMD}}}} = \frac{{HC}}{{CD}} = \frac{2}{5}$ (chung chiều cao hạ từ M xuống CD)
Suy ra $\frac{{{S_{CMA}}}}{{{S_{CMD}}}} = \frac{4}{5}$ (Tỉ số chiều cao hạ từ A xuống CN và chiều cao hạ từ D xuống CN bằng $\frac{4}{5}$)
Suy ra $\frac{{{S_{CNA}}}}{{{S_{CND}}}} = \frac{4}{5}$ nên $\frac{{AN}}{{ND}} = \frac{4}{5}$
ĐỀ THI THỬ VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM 2024
MÔN: TOÁN
Đề số 2
Nguồn: Sưu tầm
I. TRẮC NGHIỆM
Câu 1. Hiện nay, ông hơn cháu 66 tuổi. Sang năm, tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm. Tuổi cháu hiện nay là:
A. 4 tuổi B. 5 tuổi C. 6 tuổi D. 7 tuổi
Câu 2. Một số có ba chữ số có tích các chữ số là 7. Tổng các chữ số của số đó là
A. 9 B. 8 C. 7 D. 6
Câu 3. Dũng sinh vào tháng 4. Năm 2020, sinh nhật Dũng vào ngày Chủ nhật. Năm 2024 sinh nhật Dũng vào thứ mấy?
A. Thứ năm B. Thứ sáu C. Thứ bảy D. Chủ nhật
Câu 4. Một tấm bìa hình chữ nhật có chu vi bằng 68cm, chiều dài bằng $\frac{{12}}{5}$ chiều rộng. Diện tích tấm bìa này bằng $\frac{2}{3}$ diện tích tấm bìa hình tam giác. Biết chiều cao tấm bìa hình tam giác là 18 cm, độ dài cạnh đáy tương ứng bằng:
A. 10 cm B. 20 cm C. 40 cm D. 80 cm
Câu 5. Hàng ngày, An đi từ nhà lúc 7 giờ 25 phút và tới trường lúc 8 giờ kém 20 phút. Sáng nay do ngủ dậy muộn nên 7 giờ rưỡi An mới xuất phát. An tính rằng để đến trường đúng giờ, mỗi phút bạn phải đi nhanh hơn hàng ngày 50m. Độ dài quãng đường từ nhà An đến trường là:
A. 2,5 cm B. 2 km C. 1,5 km D. 1 km
II. TỰ LUẬN
Câu 1. Đầu năm học, bốn bạn An, Toàn, Giao, Thông mua một số quyền vờ. Số vở của An bằng $\frac{1}{2}$ tổng số vở của ba bạn còn lại. Số vở của Toàn bằng $\frac{1}{5}$ tổng số vở của ba bạn còn lại. Số vở của Giao bằng $\frac{3}{2}$ số vở của Thông. Tính số vở của mỗi bạn, biết An có nhiều hơn toàn 10 quyển vở.
Câu 2. Cho hình thang vuông ABCD có góc B và góc C vuông, đáy nhỏ AB bằng $\frac{2}{5}$ đáy lớn CD, kẻ chiều cao AH.
a) Tính tỉ số của diện tích hình chữ nhật ABCH và diện tích tam giác AHD.
b) Lấy M trên AH sao cho $MH = \frac{1}{3}AH$, kéo dài CM cắt AD tại N. Tính tỉ số của AN và ND.
HƯỚNG DẪN GIẢI CHI TIẾT
I. TRẮC NGHIỆM
Câu 1. Hiện nay, ông hơn cháu 66 tuổi. Sang năm, tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm. Tuổi cháu hiện nay là:
A. 4 tuổi B. 5 tuổi C. 6 tuổi D. 7 tuổi
Lời giải
Vì năm sau, tuổi cháu có bao nhiêu tháng thì tuổi ông là bấy nhiêu năm, mà mỗi năm có 12 tháng, nên năm sau tuổi ông gấp 12 lần tuổi cháu.
Ông hơn cháu 66 tuổi nên tuổi cháu năm sau là: 66 : (12 -1) ´1 = 6 (tuổi)
Tuổi cháu hiện nay là: 6 – 1 = 5 (tuổi)
Đáp án: B
Câu 2. Một số có ba chữ số có tích các chữ số là 7. Tổng các chữ số của số đó là
A. 9 B. 8 C. 7 D. 6
Lời giải:
Ta có: 7 = 7 x 1 x 1
Vì tích các chữ số của số đó là 7 nên số đó là 117 hoặc 171 hoặc 711. Tổng các chữ số của số đó là:
1 + 1 + 7 = 9
Đáp án: A
Câu 3. Dũng sinh vào tháng 4. Năm 2020, sinh nhật Dũng vào ngày Chủ nhật. Năm 2024 sinh nhật Dũng vào thứ mấy?
A. Thứ năm B. Thứ sáu C. Thứ bảy D. Chủ nhật
Lời giải:
Mỗi năm có 365 ngày, nhưng năm 2024 là năm nhuận nên sẽ có ngày 29 tháng 2.
Số ngày từ sinh nhật năm 2020 đến sinh nhật năm 2024 của Dũng là: 365´ 4 + 1 = 1461 (ngày)
Ta có 1461 : 7 = 208 (dư 5)
Ta thấy, số ngày chia chia hết cho 7 là chủ nhật nên số ngày chia 7 dư 5 là thứ sáu. Vậy sinh nhật Dũng năm 2024 là Thứ Sáu.
Đáp án: B
Câu 4. Một tấm bìa hình chữ nhật có chu vi bằng 68cm, chiều dài bằng $\frac{{12}}{5}$ chiều rộng. Diện tích tấm bìa này bằng $\frac{2}{3}$ diện tích tấm bìa hình tam giác. Biết chiều cao tấm bìa hình tam giác là 18 cm, độ dài cạnh đáy tương ứng bằng:
A. 10 cm B. 20 cm C. 40 cm D. 80 cm
Lời giải
Nửa chu vi hình chữ nhật là 68 : 2 = 34 (cm)
Chiều dài hình chữ nhật là 34 : (12 + 5) x 12 = 24 (cm)
Chiều dài hình chữ nhật là 34 – 24 = 10 (cm)
Diện tích tấm bìa hình chữ nhật là 24 x 10 = 240 (cm2)
Diện tích tấm bìa hình tam giác là:
$240:\frac{2}{3} = 360$ (cm2)
Độ dài cạnh đáy tương ứng bằng: 360 x 2 : 18 = 40 (cm)
Đáp án: C
Câu 5. Hàng ngày, An đi từ nhà lúc 7 giờ 25 phút và tới trường lúc 8 giờ kém 20 phút. Sáng nay do ngủ dậy muộn nên 7 giờ rưỡi An mới xuất phát. An tính rằng để đến trường đúng giờ, mỗi phút bạn phải đi nhanh hơn hàng ngày 50m. Độ dài quãng đường từ nhà An đến trường là:
A. 2,5 cm B. 2 km C. 1,5 km D. 1 km
Lời giải
Đổi: 8 giờ kém 20 phút = 7 giờ 40 phút
Thời gian An đi từ nhà đến trường là 7 giờ 40 phút – 7 giờ 25 phút = 15 phút
Thời gian bạn An phải đi hôm nay là: 7 giờ 40 phút – 7 giờ 30 phút = 10 phút
Trên cùng quãng đường AB thì thời gian và vận tốc là hai đại lượng tỉ lệ nghịch.
Tỉ số thời gian An đi hôm nay và mọi ngày An đi là: $\frac{{10}}{{15}} = \frac{2}{3}$
Tỉ số vận tốc của An hôm nay và mọi ngày là: $\frac{3}{2}$
Vận tốc của An hôm nay là: 50 : (3 - 2) ´ 3 = 150 (m/phút)
Quảng đường từ nhà đến trường là: 150´10 =1500 (m) = 1,5 km
Đáp án: C
II. TỰ LUẬN
Câu 1. Đầu năm học, bốn bạn An, Toàn, Giao, Thông mua một số quyển vở. Số vở của An bằng $\frac{1}{2}$ tổng số vở của ba bạn còn lại. Số vở của Toàn bằng $\frac{1}{5}$ tổng số vở của ba bạn còn lại. Số vở của Giao bằng $\frac{3}{2}$ số vở của Thông. Tính số vở của mỗi bạn, biết An có nhiều hơn Toàn 10 quyển vở.
Cách giải:
Số vở của An bằng $\frac{1}{2}$ tổng số vở của ba bạn còn lại nên số vở của An bằng $\frac{1}{3}$ tổng số vở.
Số vở của Toàn bằng $\frac{1}{5}$ tổng số vở của ba bạn còn lại nên số vở của Toàn bằng $\frac{1}{6}$ tổng số vở.
Biết An có nhiều hơn Toàn 10 quyển vở.
10 quyển vở ứng với phân số $\frac{1}{3} - \frac{1}{6} = \frac{1}{6}$ (tổng số vở)
Tổng số vở của 4 bạn là: $10:\frac{1}{6} = 60$(quyển vở)
Số vở của An là $60 \times \frac{1}{3} = 20$ (quyển)
Số vở của Toàn là 20 – 10 = 10 (quyển)
Số vở của Giao và Thông là 60 – 20 – 10 = 30 (quyển)
Ta có: Số vở của Giao bằng $\frac{3}{2}$ số vở của Thông.
Số vở của Giao là 30 : (3 + 2) x 3 = 18 (quyển)
Số vở của Thông là 30 – 18 = 12 (quyển)
Đáp số: An: 20 quyển
Toàn: 10 quyển
Giao: 18 quyển
Thông: 12 quyển
Câu 2. Cho hình thang vuông ABCD có góc B và góc C vuông, đáy nhỏ AB bằng $\frac{2}{5}$ đáy lớn CD, kẻ chiều cao AH.
a) Tính tỉ số của diện tích hình chữ nhật ABCH và diện tích tam giác AHD.
b) Lấy M trên AH sao cho $MH = \frac{1}{3}AH$, kéo dài CM cắt AD tại N. Tính tỉ số của AN và ND.
Lời giải
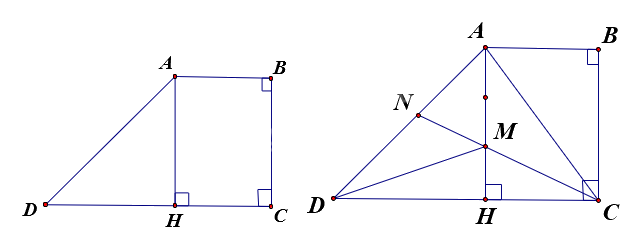
a) Ta có ${S_{ABCH}} = AB \times AH$ và ${S_{AHD}} = \frac{{AH \times HD}}{2}$
Mà $AB = \frac{2}{5}CD$ nên $AB = \frac{2}{3}HD$
Suy ra ${S_{ABCH}} = \frac{2}{3}HD \times AH = \frac{{2 \times HD \times AH}}{3}$. Từ đó suy ra $\frac{{{S_{ABCH}}}}{{{S_{AHD}}}} = \frac{4}{3}$
b) Ta có $\frac{{SCMA}}{{SCMH}} = \frac{{MA}}{{MH}} = \frac{2}{1} = \frac{4}{2}$ (chung chiều cao hạ từ C xuống AH)
$\frac{{{S_{CMH}}}}{{{S_{CMD}}}} = \frac{{HC}}{{CD}} = \frac{2}{5}$ (chung chiều cao hạ từ M xuống CD)
Suy ra $\frac{{{S_{CMA}}}}{{{S_{CMD}}}} = \frac{4}{5}$ (Tỉ số chiều cao hạ từ A xuống CN và chiều cao hạ từ D xuống CN bằng $\frac{4}{5}$)
Suy ra $\frac{{{S_{CNA}}}}{{{S_{CND}}}} = \frac{4}{5}$ nên $\frac{{AN}}{{ND}} = \frac{4}{5}$
Kỳ thi tuyển sinh vào lớp 6 trường chuyên Ngoại ngữ là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc luyện tập với các đề thi thử là vô cùng cần thiết. Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 2) mà giaitoan.edu.vn cung cấp là một công cụ hữu ích giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn khi bước vào phòng thi.
Đề thi thử này bao gồm các dạng bài tập thường gặp trong kỳ thi tuyển sinh vào lớp 6 trường chuyên Ngoại ngữ, bao gồm:
Đề thi tập trung vào các chủ đề chính sau:
Để giải đề thi hiệu quả, các em cần lưu ý những điều sau:
Việc luyện tập với các đề thi thử không chỉ giúp các em làm quen với cấu trúc đề thi mà còn giúp các em:
Để đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 6 trường chuyên Ngoại ngữ, các em nên:
Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 2) là một công cụ hữu ích giúp các em chuẩn bị tốt nhất cho kỳ thi tuyển sinh. Hãy luyện tập chăm chỉ và tự tin vào bản thân, chắc chắn các em sẽ đạt được kết quả tốt nhất. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức!