Bài 59 Toán lớp 4 trang 18 thuộc chương trình SGK Cánh diều, tập trung vào việc ôn luyện và thực hành kỹ năng rút gọn phân số. Đây là một kiến thức nền tảng quan trọng trong chương trình Toán Tiểu học, giúp học sinh hiểu rõ hơn về cấu trúc và tính chất của phân số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong bài học này, giúp các em học sinh tự tin giải quyết các bài toán và củng cố kiến thức đã học.
Rút gọn các phân số sau về phân số tối giản: a) Quan sát cách tính của Hiếu và Thảo khi rút gọn phân số 12/18 rồi nêu nhận xét:
Video hướng dẫn giải
Rút gọn các phân số:
a) $\frac{2}{{10}}$
b) $\frac{9}{6}$
c) $\frac{5}{{20}}$
d) $\frac{6}{{16}}$
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) $\frac{2}{{10}}$ = $\frac{{2:2}}{{10:2}} = \frac{1}{5}$
b) $\frac{9}{6} = \frac{{9:3}}{{6:3}} = \frac{3}{2}$
c) $\frac{5}{{20}}$= $\frac{{5:5}}{{20:5}} = \frac{1}{4}$
d) $\frac{6}{{16}} = \frac{{6:2}}{{16:2}} = \frac{3}{8}$
Video hướng dẫn giải
a) Phân số nào trong các phân số: $\frac{1}{5}$;$\frac{7}{6}$; $\frac{9}{{19}}$; $\frac{{16}}{{32}}$ là phân số tối giản?
b) Hãy tìm ba phân số tối giản, ba phân số chưa tối giản. Rút gọn các phân số chưa tối giản vừa tìm.
Phương pháp giải:
Phân số tối giản là phân số mà cả tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác 1.
Lời giải chi tiết:
a) Các phân số tối giản là $\frac{1}{5}$; $\frac{7}{6}$; $\frac{9}{{19}}$
b) Ba phân số tối giản là: $\frac{2}{3}$; $\frac{5}{9}$; $\frac{1}{6}$
Ba phân số chưa tối giản là: $\frac{{10}}{{25}}$; $\frac{{30}}{{70}}$; $\frac{{16}}{{36}}$
Ta có:
$\frac{{10}}{{25}} = \frac{{10:5}}{{25:5}} = \frac{2}{5}$
$\frac{{30}}{{70}} = \frac{{30:10}}{{70:10}} = \frac{3}{7}$
$\frac{{16}}{{36}} = \frac{{16:4}}{{36:4}} = \frac{4}{9}$
Video hướng dẫn giải
Rút gọn các phân số sau về phân số tối giản:
a) $\frac{8}{{16}}$
b) $\frac{{10}}{{30}}$
c) $\frac{{24}}{{18}}$
d) $\frac{{20}}{{28}}$
Ghi chú: Khi rút gọn phân số, ta nên rút gọn cho đến khi nhận được phân số tối giản.
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) $\frac{8}{{16}} = \frac{{8:8}}{{16:8}} = \frac{1}{2}$
b) $\frac{{10}}{{30}} = \frac{{10:10}}{{30:10}} = \frac{1}{3}$
c) $\frac{{24}}{{18}} = \frac{{24:6}}{{18:6}} = \frac{4}{3}$
d) $\frac{{20}}{{28}} = \frac{{20:4}}{{28:4}} = \frac{5}{7}$
Video hướng dẫn giải
Một bài ôn tập có tất cả 16 câu hỏi. Bạn Gia Hân trả lời đúng 12 câu.
a) Hỏi bạn Gia Hân trả lời đúng được bao nhiêu phần số câu hỏi của bài ôn tập?
b) Rút gọn phân số ở câu a về dạng phân số tối giản.
Phương pháp giải:
a) Phân số chỉ số câu trả lời đúng của Gia Hân có tử số là số câu trả lời đúng, mẫu số là số câu hỏi của bài ôn tập.
b)
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) Gia Hân trả lời đúng được $\frac{{12}}{{16}}$ số câu hỏi của bài ôn tập.
b) $\frac{{12}}{{16}}$= $\frac{{12:4}}{{16:4}} = \frac{3}{4}$
>> Xem chi tiết: Lý thuyết: Rút gọn phân số - SGK Cánh diều
Video hướng dẫn giải
a) Quan sát cách tính của Hiếu và Thảo khi rút gọn phân số $\frac{{12}}{{18}}$ rồi nêu nhận xét:
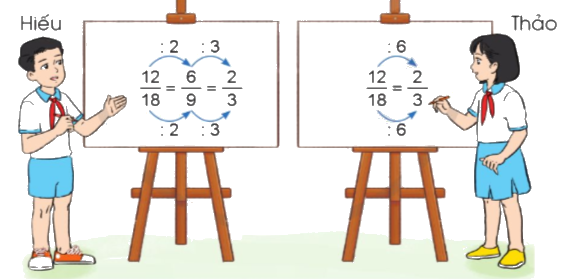
b) Rút gọn phân số $\frac{{30}}{{60}}$về dạng phân số tối giản sử dụng cách làm của Hiếu hoặc của Thảo.
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) Cách tính của Hiếu và Thảo đều đúng.
b) $\frac{{30}}{{60}} = \frac{{30:30}}{{60:30}} = \frac{1}{2}$
Video hướng dẫn giải
Rút gọn các phân số:
a) $\frac{2}{{10}}$
b) $\frac{9}{6}$
c) $\frac{5}{{20}}$
d) $\frac{6}{{16}}$
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) $\frac{2}{{10}}$ = $\frac{{2:2}}{{10:2}} = \frac{1}{5}$
b) $\frac{9}{6} = \frac{{9:3}}{{6:3}} = \frac{3}{2}$
c) $\frac{5}{{20}}$= $\frac{{5:5}}{{20:5}} = \frac{1}{4}$
d) $\frac{6}{{16}} = \frac{{6:2}}{{16:2}} = \frac{3}{8}$
Video hướng dẫn giải
Rút gọn các phân số sau về phân số tối giản:
a) $\frac{8}{{16}}$
b) $\frac{{10}}{{30}}$
c) $\frac{{24}}{{18}}$
d) $\frac{{20}}{{28}}$
Ghi chú: Khi rút gọn phân số, ta nên rút gọn cho đến khi nhận được phân số tối giản.
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) $\frac{8}{{16}} = \frac{{8:8}}{{16:8}} = \frac{1}{2}$
b) $\frac{{10}}{{30}} = \frac{{10:10}}{{30:10}} = \frac{1}{3}$
c) $\frac{{24}}{{18}} = \frac{{24:6}}{{18:6}} = \frac{4}{3}$
d) $\frac{{20}}{{28}} = \frac{{20:4}}{{28:4}} = \frac{5}{7}$
Video hướng dẫn giải
a) Phân số nào trong các phân số: $\frac{1}{5}$;$\frac{7}{6}$; $\frac{9}{{19}}$; $\frac{{16}}{{32}}$ là phân số tối giản?
b) Hãy tìm ba phân số tối giản, ba phân số chưa tối giản. Rút gọn các phân số chưa tối giản vừa tìm.
Phương pháp giải:
Phân số tối giản là phân số mà cả tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác 1.
Lời giải chi tiết:
a) Các phân số tối giản là $\frac{1}{5}$; $\frac{7}{6}$; $\frac{9}{{19}}$
b) Ba phân số tối giản là: $\frac{2}{3}$; $\frac{5}{9}$; $\frac{1}{6}$
Ba phân số chưa tối giản là: $\frac{{10}}{{25}}$; $\frac{{30}}{{70}}$; $\frac{{16}}{{36}}$
Ta có:
$\frac{{10}}{{25}} = \frac{{10:5}}{{25:5}} = \frac{2}{5}$
$\frac{{30}}{{70}} = \frac{{30:10}}{{70:10}} = \frac{3}{7}$
$\frac{{16}}{{36}} = \frac{{16:4}}{{36:4}} = \frac{4}{9}$
Video hướng dẫn giải
a) Quan sát cách tính của Hiếu và Thảo khi rút gọn phân số $\frac{{12}}{{18}}$ rồi nêu nhận xét:
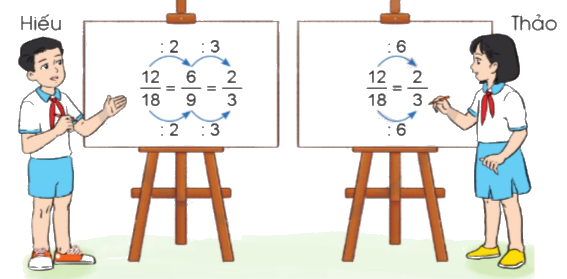
b) Rút gọn phân số $\frac{{30}}{{60}}$về dạng phân số tối giản sử dụng cách làm của Hiếu hoặc của Thảo.
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) Cách tính của Hiếu và Thảo đều đúng.
b) $\frac{{30}}{{60}} = \frac{{30:30}}{{60:30}} = \frac{1}{2}$
Video hướng dẫn giải
Một bài ôn tập có tất cả 16 câu hỏi. Bạn Gia Hân trả lời đúng 12 câu.
a) Hỏi bạn Gia Hân trả lời đúng được bao nhiêu phần số câu hỏi của bài ôn tập?
b) Rút gọn phân số ở câu a về dạng phân số tối giản.
Phương pháp giải:
a) Phân số chỉ số câu trả lời đúng của Gia Hân có tử số là số câu trả lời đúng, mẫu số là số câu hỏi của bài ôn tập.
b)
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia cả tử số và mẫu số cho số đó.
Lời giải chi tiết:
a) Gia Hân trả lời đúng được $\frac{{12}}{{16}}$ số câu hỏi của bài ôn tập.
b) $\frac{{12}}{{16}}$= $\frac{{12:4}}{{16:4}} = \frac{3}{4}$
>> Xem chi tiết: Lý thuyết: Rút gọn phân số - SGK Cánh diều
Bài 59 Toán lớp 4 trang 18 thuộc chương trình SGK Cánh diều, là một bước quan trọng trong việc củng cố kiến thức về phân số cho học sinh. Bài học này tập trung vào việc rèn luyện kỹ năng rút gọn phân số, một kỹ năng cơ bản nhưng vô cùng quan trọng trong toán học.
Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho một ước chung lớn nhất của chúng. Mục đích của việc rút gọn phân số là để biểu diễn phân số ở dạng đơn giản nhất, tức là tử số và mẫu số không còn ước chung nào khác ngoài 1.
Ví dụ 1: Rút gọn phân số 12/18
Ví dụ 2: Rút gọn phân số 25/35
Dưới đây là một số bài tập để các em học sinh luyện tập kỹ năng rút gọn phân số:
Khi rút gọn phân số, cần đảm bảo rằng cả tử số và mẫu số đều chia hết cho ước chung. Nếu không, phân số sẽ không được rút gọn đúng cách. Ngoài ra, cần tìm ƯCLN của tử số và mẫu số để rút gọn phân số về dạng đơn giản nhất.
Việc rút gọn phân số có nhiều ứng dụng trong toán học và thực tế. Ví dụ, khi so sánh hai phân số, việc rút gọn chúng về dạng tối giản sẽ giúp việc so sánh trở nên dễ dàng hơn. Ngoài ra, trong các bài toán tính toán, việc rút gọn phân số có thể giúp đơn giản hóa các phép tính và giảm thiểu sai sót.
Ngoài việc rút gọn phân số, các em học sinh cũng cần nắm vững các kiến thức khác về phân số, như:
Việc nắm vững các kiến thức này sẽ giúp các em học sinh giải quyết các bài toán về phân số một cách hiệu quả và tự tin hơn.
giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức hữu ích về cách rút gọn phân số. Chúc các em học tập tốt!