Bài học Toán lớp 4 trang 56 - Bài 77: Trừ hai phân số khác mẫu số - SGK cánh diều là một phần quan trọng trong chương trình học Toán lớp 4. Bài học này giúp học sinh nắm vững phương pháp trừ hai phân số khi chúng có mẫu số khác nhau.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các bài tập luyện tập để giúp các em học sinh hiểu sâu và nắm vững kiến thức.
Rút gọn rồi tính 2/5 - 3/15 Người ta tiến hành sửa chữa vỉa hè của một đoạn đường
Video hướng dẫn giải
Rút gọn rồi tính:
a) $\frac{2}{5} - \frac{3}{{15}}$
b) $\frac{9}{{27}} - \frac{2}{9}$
c) $\frac{{18}}{{24}} - \frac{4}{8}$
d) $\frac{6}{{16}} - \frac{{10}}{{64}}$
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{2}{5} - \frac{3}{{15}} = \frac{2}{5} - \frac{1}{5} = \frac{1}{5}$
b) $\frac{9}{{27}} - \frac{2}{9} = \frac{3}{9} - \frac{2}{9} = \frac{1}{9}$
c) $\frac{{18}}{{24}} - \frac{4}{8} = \frac{3}{4} - \frac{2}{4} = \frac{1}{4}$
d) $\frac{6}{{16}} - \frac{{10}}{{64}}$ = $\frac{3}{8} - \frac{5}{{32}} = \frac{{12}}{{32}} - \frac{5}{{32}} = \frac{7}{{32}}$
>> Xem chi tiết: Lý thuyết: Trừ các phân số khác mẫu số - SGK Cánh diều
Video hướng dẫn giải
Người ta tiến hành sửa chữa vỉa hè của một đoạn đường. Ngày thứ nhất sửa được $\frac{2}{3}$ đoạn vỉa hè, ngày thứ hai sửa được $\frac{1}{6}$ đoạn vỉa hè. Hỏi ngày thứ nhất sửa được nhiều hơn ngày thứ hai bao nhiêu phần đoạn vỉa hè?

Phương pháp giải:
Ngày thứ nhất sửa được nhiều hơn ngày thứ hai số phần đoạn vỉa hè = số phần vỉa hè ngày thứ nhất sửa được – số phần vỉa hè ngày thứ hai sửa được
Lời giải chi tiết:
Ngày thứ nhất sửa được nhiều hơn ngày thứ hai số phần đoạn vỉa hè là:
$\frac{2}{3} - \frac{1}{6} = \frac{1}{2}$ (đoạn vỉa hè)
Đáp số: $\frac{1}{2}$ đoạn vỉa hè
Video hướng dẫn giải
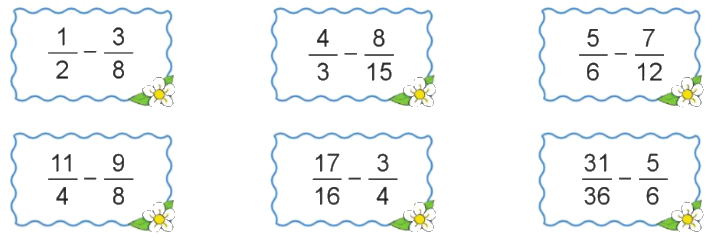
Tính:
Phương pháp giải:
Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
$\frac{1}{2} - \frac{3}{8} = \frac{4}{8} - \frac{3}{8} = \frac{1}{8}$
$\frac{4}{3} - \frac{8}{{15}} = \frac{{20}}{{15}} - \frac{8}{{15}} = \frac{{12}}{{15}} = \frac{4}{5}$
$\frac{5}{6} - \frac{7}{{12}} = \frac{{10}}{{12}} - \frac{7}{{12}} = \frac{3}{{12}} = \frac{1}{4}$
$\frac{{11}}{4} - \frac{9}{8} = \frac{{22}}{8} - \frac{9}{8} = \frac{{13}}{8}$
$\frac{{17}}{{16}} - \frac{3}{4} = \frac{{17}}{{16}} - \frac{{12}}{{16}} = \frac{5}{{16}}$
$\frac{{31}}{{36}} - \frac{5}{6} = \frac{{31}}{{36}} - \frac{{30}}{{36}} = \frac{1}{{36}}$
Video hướng dẫn giải
a) Trong một ngày thời gian để học và ngủ của bạn Dũng là $\frac{5}{8}$ngày, trong đó thời gian học của Dũng là $\frac{1}{4}$ngày. Hỏi thời gian ngủ của bạn Dũng là bao nhiêu phần một ngày?
b) Em đã dành bao nhiêu phần thời gian của một ngày để học? Thời gian cho các hoạt động khác là bao nhiêu phần một ngày?

Phương pháp giải:
a) Số phần thời gian ngủ trong một ngày = số phần thời gian để học và ngủ – số phần thời gian học
b) Em liên hệ bản thân để trả lời câu hỏi
Lời giải chi tiết:
a) Thời gian ngủ của bạn Dũng trong một ngày là:
$\frac{5}{8} - \frac{1}{4} = \frac{3}{8}$ (ngày)
Đáp số: $\frac{3}{8}$ ngày
b) Em đã dành $\frac{1}{4}$ngày để học và $\frac{3}{4}$ ngày cho các hoạt động khác.
Video hướng dẫn giải
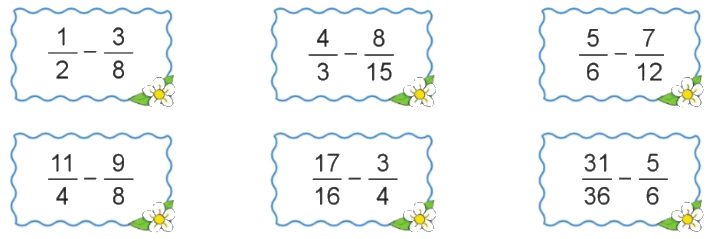
Tính:
Phương pháp giải:
Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
$\frac{1}{2} - \frac{3}{8} = \frac{4}{8} - \frac{3}{8} = \frac{1}{8}$
$\frac{4}{3} - \frac{8}{{15}} = \frac{{20}}{{15}} - \frac{8}{{15}} = \frac{{12}}{{15}} = \frac{4}{5}$
$\frac{5}{6} - \frac{7}{{12}} = \frac{{10}}{{12}} - \frac{7}{{12}} = \frac{3}{{12}} = \frac{1}{4}$
$\frac{{11}}{4} - \frac{9}{8} = \frac{{22}}{8} - \frac{9}{8} = \frac{{13}}{8}$
$\frac{{17}}{{16}} - \frac{3}{4} = \frac{{17}}{{16}} - \frac{{12}}{{16}} = \frac{5}{{16}}$
$\frac{{31}}{{36}} - \frac{5}{6} = \frac{{31}}{{36}} - \frac{{30}}{{36}} = \frac{1}{{36}}$
Video hướng dẫn giải
Rút gọn rồi tính:
a) $\frac{2}{5} - \frac{3}{{15}}$
b) $\frac{9}{{27}} - \frac{2}{9}$
c) $\frac{{18}}{{24}} - \frac{4}{8}$
d) $\frac{6}{{16}} - \frac{{10}}{{64}}$
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{2}{5} - \frac{3}{{15}} = \frac{2}{5} - \frac{1}{5} = \frac{1}{5}$
b) $\frac{9}{{27}} - \frac{2}{9} = \frac{3}{9} - \frac{2}{9} = \frac{1}{9}$
c) $\frac{{18}}{{24}} - \frac{4}{8} = \frac{3}{4} - \frac{2}{4} = \frac{1}{4}$
d) $\frac{6}{{16}} - \frac{{10}}{{64}}$ = $\frac{3}{8} - \frac{5}{{32}} = \frac{{12}}{{32}} - \frac{5}{{32}} = \frac{7}{{32}}$
Video hướng dẫn giải
Người ta tiến hành sửa chữa vỉa hè của một đoạn đường. Ngày thứ nhất sửa được $\frac{2}{3}$ đoạn vỉa hè, ngày thứ hai sửa được $\frac{1}{6}$ đoạn vỉa hè. Hỏi ngày thứ nhất sửa được nhiều hơn ngày thứ hai bao nhiêu phần đoạn vỉa hè?

Phương pháp giải:
Ngày thứ nhất sửa được nhiều hơn ngày thứ hai số phần đoạn vỉa hè = số phần vỉa hè ngày thứ nhất sửa được – số phần vỉa hè ngày thứ hai sửa được
Lời giải chi tiết:
Ngày thứ nhất sửa được nhiều hơn ngày thứ hai số phần đoạn vỉa hè là:
$\frac{2}{3} - \frac{1}{6} = \frac{1}{2}$ (đoạn vỉa hè)
Đáp số: $\frac{1}{2}$ đoạn vỉa hè
Video hướng dẫn giải
a) Trong một ngày thời gian để học và ngủ của bạn Dũng là $\frac{5}{8}$ngày, trong đó thời gian học của Dũng là $\frac{1}{4}$ngày. Hỏi thời gian ngủ của bạn Dũng là bao nhiêu phần một ngày?
b) Em đã dành bao nhiêu phần thời gian của một ngày để học? Thời gian cho các hoạt động khác là bao nhiêu phần một ngày?

Phương pháp giải:
a) Số phần thời gian ngủ trong một ngày = số phần thời gian để học và ngủ – số phần thời gian học
b) Em liên hệ bản thân để trả lời câu hỏi
Lời giải chi tiết:
a) Thời gian ngủ của bạn Dũng trong một ngày là:
$\frac{5}{8} - \frac{1}{4} = \frac{3}{8}$ (ngày)
Đáp số: $\frac{3}{8}$ ngày
b) Em đã dành $\frac{1}{4}$ngày để học và $\frac{3}{4}$ ngày cho các hoạt động khác.
>> Xem chi tiết: Lý thuyết: Trừ các phân số khác mẫu số - SGK Cánh diều
Bài 77 trong sách giáo khoa Toán lớp 4 cánh diều tập trung vào kỹ năng trừ hai phân số có mẫu số khác nhau. Đây là một kỹ năng quan trọng, nền tảng cho các phép toán phức tạp hơn ở các lớp trên. Để giải quyết bài toán này, học sinh cần nắm vững quy tắc tìm mẫu số chung và quy đồng mẫu số trước khi thực hiện phép trừ.
Trước khi đi vào giải bài tập cụ thể, chúng ta cùng ôn lại lý thuyết cơ bản:
Để trừ hai phân số có mẫu số khác nhau, ta thực hiện các bước sau:
Ví dụ 1: Tính \frac{2}{3} - \frac{1}{4}
Giải:
Dưới đây là một số bài tập tương tự để các em luyện tập:
Ngoài việc trừ hai phân số khác mẫu số, các em cũng cần làm quen với các phép toán khác liên quan đến phân số như cộng, nhân, chia phân số. Việc nắm vững các phép toán này sẽ giúp các em giải quyết các bài toán phức tạp hơn một cách dễ dàng.
Khi giải bài tập về phân số, các em cần chú ý:
Bài 77 Toán lớp 4 trang 56 - Bài 77: Trừ hai phân số khác mẫu số - SGK cánh diều là một bài học quan trọng giúp các em học sinh củng cố kiến thức về phân số và rèn luyện kỹ năng giải toán. Hy vọng với những hướng dẫn chi tiết và bài tập luyện tập trên, các em sẽ nắm vững kiến thức và tự tin giải các bài toán tương tự.