Chào mừng các em học sinh lớp 4 đến với bài học Toán lớp 4 trang 28 - Bài 64: Luyện tập chung của sách giáo khoa Cánh diều. Bài học này là cơ hội để các em ôn tập và củng cố kiến thức đã học về các phép tính, giải toán có lời văn và các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong bài học này, giúp các em tự tin hơn trong việc học tập và làm bài.
Nêu phân số chỉ phân số đã tô màu trong mỗi hình sau: a) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):
Video hướng dẫn giải
Trong các phân số $\frac{1}{4};\,\,\frac{6}{5};\,\,\frac{4}{{10}};\,\,\frac{{16}}{9};\,\,\frac{{10}}{{20}};\,\,\frac{8}{{18}}$
a) Phân số nào là phân số tối giản?
b) Rút gọn các phân số chưa tối giản
Phương pháp giải:
- Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1
- Cách rút gọn phân số:
+ Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
+ Chia tử số và mẫy số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) Các phân số tối giản là $\frac{1}{4};\,\,\frac{6}{5};\,\,\frac{{16}}{9}$
b) Các phân số chưa tối giản là $\frac{4}{{10}};\,\,\frac{{10}}{{20}};\,\,\frac{8}{{18}}$
$\frac{4}{{10}} = \frac{{4:2}}{{10:2}} = \frac{2}{5}$
$\frac{{10}}{{20}} = \frac{{10:10}}{{20:10}} = \frac{1}{2}$
$\frac{8}{{18}} = \frac{{8:2}}{{18:2}} = \frac{4}{9}$
Video hướng dẫn giải
Quy đồng mẫu số hai phân số:
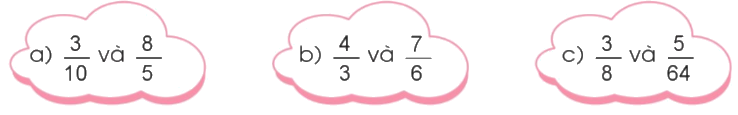
Phương pháp giải:
- Tìm mẫu số chung- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) Ta có: $\frac{8}{5} = \frac{{8 \times 2}}{{5 \times 2}} = \frac{{16}}{{10}}$ ; Giữ nguyên phân số $\frac{3}{{10}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{{10}}$ và $\frac{8}{5}$ ta được hai phân số $\frac{3}{{10}}$ và $\frac{{16}}{{10}}$
b) $\frac{4}{3} = \frac{{4 \times 2}}{{3 \times 2}} = \frac{8}{6}$ ; Giữ nguyên phân số $\frac{7}{6}$
Vậy quy đồng mẫu số hai phân số $\frac{4}{3}$ và $\frac{7}{6}$ ta được hai phân số $\frac{8}{6}$ và $\frac{7}{6}$
c) $\frac{3}{8} = \frac{{3 \times 8}}{{8 \times 8}} = \frac{{24}}{{64}}$ ; Giữ nguyên phân số $\frac{5}{{64}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{8}$ và $\frac{5}{{64}}$ ta được hai phân số $\frac{{24}}{{64}}$ và $\frac{5}{{64}}$
Video hướng dẫn giải
a) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):

b) Viết các số sau dưới dạng phân số có mẫu số là 1:

Phương pháp giải:
a) Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
b) Mọi số tự nhiên có thể viết thành một phân số có tử số là số tự nhiên đó và mẫu số bằng 1.
Lời giải chi tiết:
a) 3 : 8 = $\frac{3}{8}$ ; 8 : 9 = $\frac{8}{9}$
4 : 7 = $\frac{4}{7}$ ; 12 : 5 = $\frac{{12}}{5}$
b) $7 = \frac{7}{1}$;$9 = \frac{9}{1}$;$21 = \frac{{21}}{1}$; $40 = \frac{{40}}{1}$
Video hướng dẫn giải
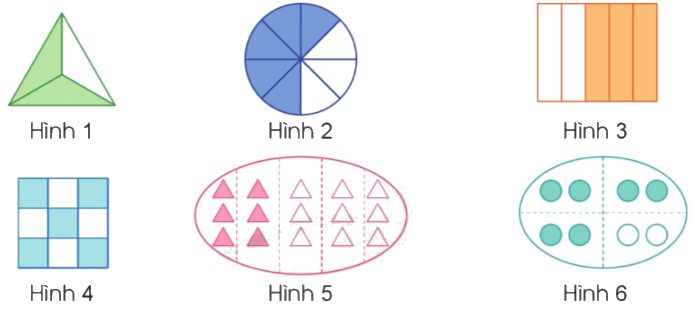
Nêu phân số chỉ số phần đã tô màu trong mỗi hình sau:
Phương pháp giải:
Phân số chỉ số phần đã tô màu có tử số là số phần tô màu, mẫu số là số phần bằng nhau của hình đó.
Lời giải chi tiết:
Hình 1: $\frac{2}{3}$ ; Hình 2: $\frac{5}{8}$
Hình 3: $\frac{3}{5}$ ; Hình 4: $\frac{5}{9}$
Hình 5: $\frac{2}{5}$ ; Hình 6: $\frac{3}{4}$
Video hướng dẫn giải
a)
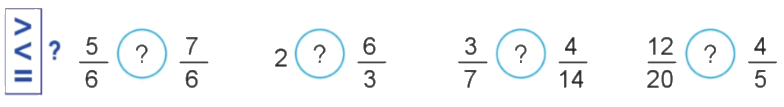
b) Viết các phân số sau theo thứ tự từ lớn đến bé:

Phương pháp giải:
a) Muốn so sánh các phân số khác mẫu số, ta có thể quy đồng mẫu số các phân số đó, rồi so sánh các tử số của phân số mới.
b) So sánh các phân số rồi sắp xếp theo thứ tự từ lớn đến bé
Lời giải chi tiết:
a)
+) $\frac{5}{6} < \frac{7}{6}$
+) 2 = $\frac{6}{3}$
+) $\frac{3}{7}$ và $\frac{4}{{14}}$
Ta có: $\frac{3}{7} = \frac{{3 \times 2}}{{7 \times 2}} = \frac{6}{{14}}$
Vì $\frac{6}{{14}} > \frac{4}{{14}}$ nên $\frac{3}{7} > \frac{4}{{14}}$
+) $\frac{{12}}{{20}}$ và $\frac{4}{5}$
Ta có: $\frac{4}{5} = \frac{{4 \times 4}}{{5 \times 4}} = \frac{{16}}{{20}}$ ; Giữ nguyên phân số: $\frac{{12}}{{20}}$
Vì $\frac{{12}}{{20}}$ < $\frac{{16}}{{20}}$ nên $\frac{{12}}{{20}}$ < $\frac{4}{5}$
Vậy ta có kết quả như sau:
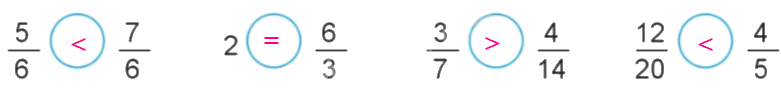
b) Quy đồng ba phân số$\frac{1}{{13}};\,\,\frac{{25}}{{13}};\,\,\frac{4}{{39}}$
$\frac{1}{{13}} = \frac{{1 \times 3}}{{13 \times 3}} = \frac{3}{{39}}$
$\frac{{25}}{{13}} = \frac{{25 \times 3}}{{13 \times 3}} = \frac{{75}}{{39}}$ ; Giữ nguyên phân số $\frac{4}{{39}}$
Vì $\frac{{75}}{{39}} > \frac{4}{{39}} > \frac{3}{{39}}$ nên $\frac{{25}}{{13}} > \frac{4}{{39}} > \frac{1}{{13}}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{{25}}{{13}};\,\,\frac{4}{{39}};\,\,\frac{1}{{13}}$
Quy đồng ba phân số $\frac{2}{8};\,\,\frac{7}{4};\,\,\frac{9}{{16}}$
$\frac{2}{8} = \frac{{2 \times 2}}{{8 \times 2}} = \frac{4}{{16}}$
$\frac{7}{4} = \frac{{7 \times 4}}{{4 \times 4}} = \frac{{28}}{{16}}$ ; Giữ nguyên phân số $\frac{9}{{16}}$
Vì $\frac{{28}}{{16}} > \frac{9}{{16}} > \frac{4}{{16}}$ nên $\frac{7}{4} > \frac{9}{{16}} > \frac{2}{8}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{7}{4};\,\,\frac{9}{{16}};\,\,\frac{2}{8}$
Video hướng dẫn giải
Quan sát hình vẽ, nêu phân số thích hợp:
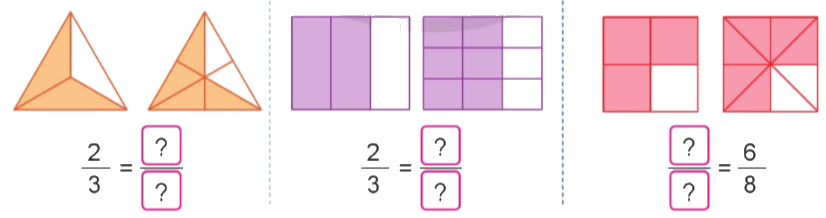
Phương pháp giải:
Quan sát hình vẽ rồi viết phân số bằng phân số đã cho.
Lời giải chi tiết:
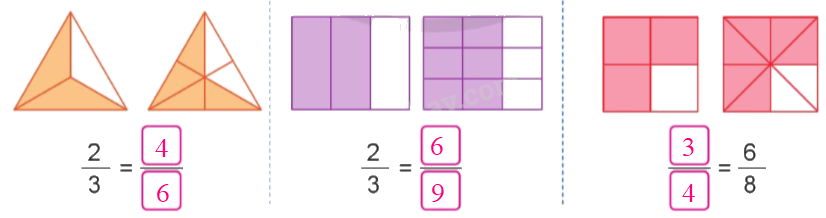
Video hướng dẫn giải
Bức rèm trong hình vẽ nào dưới đây che $\frac{3}{4}$ cửa sổ?
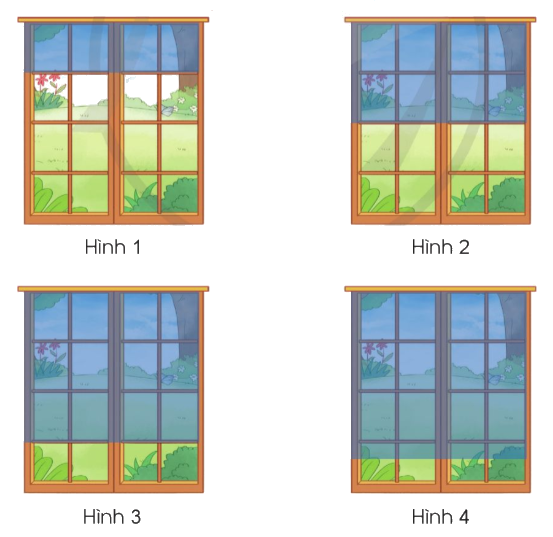
Phương pháp giải:
Quan sát rồi tìm hình vẽ có bức rèm che $\frac{3}{4}$ cửa sổ.
Lời giải chi tiết:
Bức rèm ở hình 3 che $\frac{3}{4}$ cửa sổ.
Video hướng dẫn giải
Nêu phân số chỉ số phần đã tô màu trong mỗi hình sau:
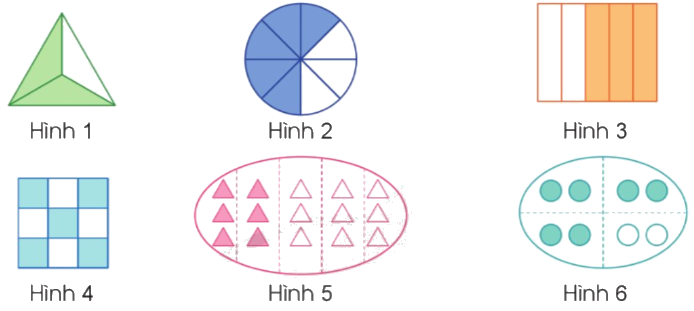
Phương pháp giải:
Phân số chỉ số phần đã tô màu có tử số là số phần tô màu, mẫu số là số phần bằng nhau của hình đó.
Lời giải chi tiết:
Hình 1: $\frac{2}{3}$ ; Hình 2: $\frac{5}{8}$
Hình 3: $\frac{3}{5}$ ; Hình 4: $\frac{5}{9}$
Hình 5: $\frac{2}{5}$ ; Hình 6: $\frac{3}{4}$
Video hướng dẫn giải
a) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):

b) Viết các số sau dưới dạng phân số có mẫu số là 1:

Phương pháp giải:
a) Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
b) Mọi số tự nhiên có thể viết thành một phân số có tử số là số tự nhiên đó và mẫu số bằng 1.
Lời giải chi tiết:
a) 3 : 8 = $\frac{3}{8}$ ; 8 : 9 = $\frac{8}{9}$
4 : 7 = $\frac{4}{7}$ ; 12 : 5 = $\frac{{12}}{5}$
b) $7 = \frac{7}{1}$;$9 = \frac{9}{1}$;$21 = \frac{{21}}{1}$; $40 = \frac{{40}}{1}$
Video hướng dẫn giải
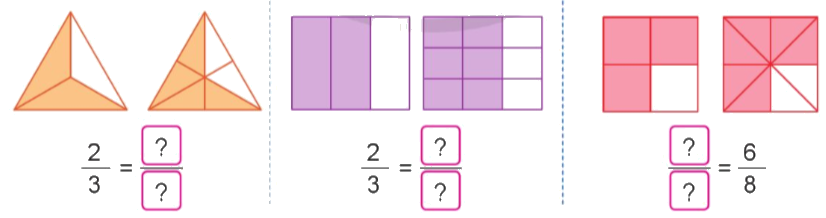
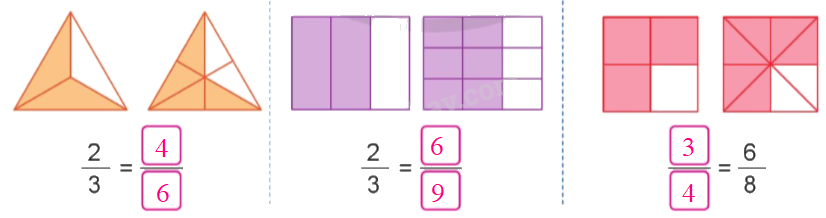
Quan sát hình vẽ, nêu phân số thích hợp:
Phương pháp giải:
Quan sát hình vẽ rồi viết phân số bằng phân số đã cho.
Lời giải chi tiết:
Video hướng dẫn giải
Trong các phân số $\frac{1}{4};\,\,\frac{6}{5};\,\,\frac{4}{{10}};\,\,\frac{{16}}{9};\,\,\frac{{10}}{{20}};\,\,\frac{8}{{18}}$
a) Phân số nào là phân số tối giản?
b) Rút gọn các phân số chưa tối giản
Phương pháp giải:
- Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1
- Cách rút gọn phân số:
+ Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
+ Chia tử số và mẫy số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) Các phân số tối giản là $\frac{1}{4};\,\,\frac{6}{5};\,\,\frac{{16}}{9}$
b) Các phân số chưa tối giản là $\frac{4}{{10}};\,\,\frac{{10}}{{20}};\,\,\frac{8}{{18}}$
$\frac{4}{{10}} = \frac{{4:2}}{{10:2}} = \frac{2}{5}$
$\frac{{10}}{{20}} = \frac{{10:10}}{{20:10}} = \frac{1}{2}$
$\frac{8}{{18}} = \frac{{8:2}}{{18:2}} = \frac{4}{9}$
Video hướng dẫn giải
Quy đồng mẫu số hai phân số:
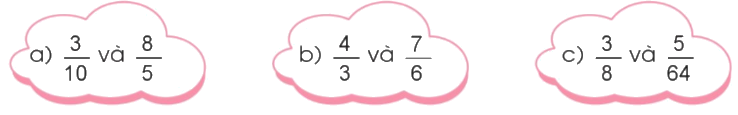
Phương pháp giải:
- Tìm mẫu số chung- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) Ta có: $\frac{8}{5} = \frac{{8 \times 2}}{{5 \times 2}} = \frac{{16}}{{10}}$ ; Giữ nguyên phân số $\frac{3}{{10}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{{10}}$ và $\frac{8}{5}$ ta được hai phân số $\frac{3}{{10}}$ và $\frac{{16}}{{10}}$
b) $\frac{4}{3} = \frac{{4 \times 2}}{{3 \times 2}} = \frac{8}{6}$ ; Giữ nguyên phân số $\frac{7}{6}$
Vậy quy đồng mẫu số hai phân số $\frac{4}{3}$ và $\frac{7}{6}$ ta được hai phân số $\frac{8}{6}$ và $\frac{7}{6}$
c) $\frac{3}{8} = \frac{{3 \times 8}}{{8 \times 8}} = \frac{{24}}{{64}}$ ; Giữ nguyên phân số $\frac{5}{{64}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{8}$ và $\frac{5}{{64}}$ ta được hai phân số $\frac{{24}}{{64}}$ và $\frac{5}{{64}}$
Video hướng dẫn giải
a)
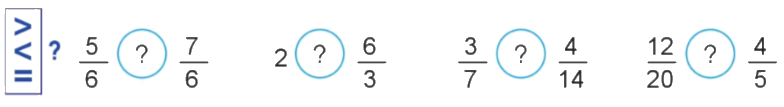
b) Viết các phân số sau theo thứ tự từ lớn đến bé:

Phương pháp giải:
a) Muốn so sánh các phân số khác mẫu số, ta có thể quy đồng mẫu số các phân số đó, rồi so sánh các tử số của phân số mới.
b) So sánh các phân số rồi sắp xếp theo thứ tự từ lớn đến bé
Lời giải chi tiết:
a)
+) $\frac{5}{6} < \frac{7}{6}$
+) 2 = $\frac{6}{3}$
+) $\frac{3}{7}$ và $\frac{4}{{14}}$
Ta có: $\frac{3}{7} = \frac{{3 \times 2}}{{7 \times 2}} = \frac{6}{{14}}$
Vì $\frac{6}{{14}} > \frac{4}{{14}}$ nên $\frac{3}{7} > \frac{4}{{14}}$
+) $\frac{{12}}{{20}}$ và $\frac{4}{5}$
Ta có: $\frac{4}{5} = \frac{{4 \times 4}}{{5 \times 4}} = \frac{{16}}{{20}}$ ; Giữ nguyên phân số: $\frac{{12}}{{20}}$
Vì $\frac{{12}}{{20}}$ < $\frac{{16}}{{20}}$ nên $\frac{{12}}{{20}}$ < $\frac{4}{5}$
Vậy ta có kết quả như sau:
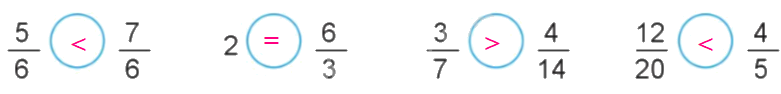
b) Quy đồng ba phân số$\frac{1}{{13}};\,\,\frac{{25}}{{13}};\,\,\frac{4}{{39}}$
$\frac{1}{{13}} = \frac{{1 \times 3}}{{13 \times 3}} = \frac{3}{{39}}$
$\frac{{25}}{{13}} = \frac{{25 \times 3}}{{13 \times 3}} = \frac{{75}}{{39}}$ ; Giữ nguyên phân số $\frac{4}{{39}}$
Vì $\frac{{75}}{{39}} > \frac{4}{{39}} > \frac{3}{{39}}$ nên $\frac{{25}}{{13}} > \frac{4}{{39}} > \frac{1}{{13}}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{{25}}{{13}};\,\,\frac{4}{{39}};\,\,\frac{1}{{13}}$
Quy đồng ba phân số $\frac{2}{8};\,\,\frac{7}{4};\,\,\frac{9}{{16}}$
$\frac{2}{8} = \frac{{2 \times 2}}{{8 \times 2}} = \frac{4}{{16}}$
$\frac{7}{4} = \frac{{7 \times 4}}{{4 \times 4}} = \frac{{28}}{{16}}$ ; Giữ nguyên phân số $\frac{9}{{16}}$
Vì $\frac{{28}}{{16}} > \frac{9}{{16}} > \frac{4}{{16}}$ nên $\frac{7}{4} > \frac{9}{{16}} > \frac{2}{8}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{7}{4};\,\,\frac{9}{{16}};\,\,\frac{2}{8}$
Video hướng dẫn giải
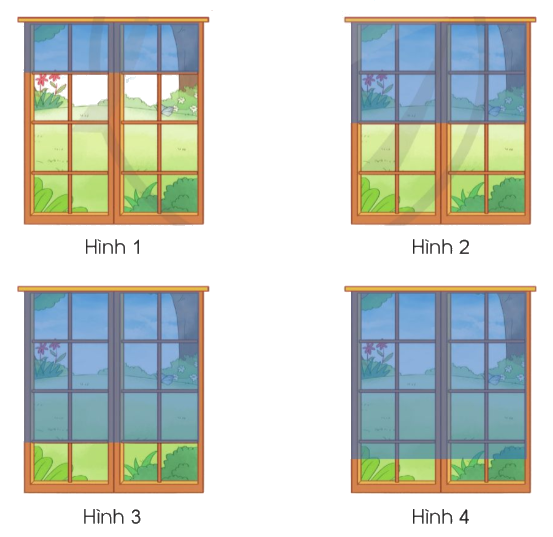
Bức rèm trong hình vẽ nào dưới đây che $\frac{3}{4}$ cửa sổ?
Phương pháp giải:
Quan sát rồi tìm hình vẽ có bức rèm che $\frac{3}{4}$ cửa sổ.
Lời giải chi tiết:
Bức rèm ở hình 3 che $\frac{3}{4}$ cửa sổ.
Bài 64: Luyện tập chung là một bài học quan trọng trong chương trình Toán lớp 4, giúp học sinh ôn lại các kiến thức đã học trong chương. Bài học này bao gồm nhiều dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết.
Bài 64 Luyện tập chung bao gồm các dạng bài tập sau:
Bài 1: Để giải các phép tính cộng, trừ, nhân, chia số có nhiều chữ số, các em cần thực hiện các bước sau:
Bài 2: Để giải các bài toán có lời văn, các em cần thực hiện các bước sau:
Bài 3: Để giải bài toán tìm số chưa biết, các em cần sử dụng các phép tính ngược lại để tìm ra số đó.
Bài 4: Để so sánh số, các em cần sử dụng các dấu >, <, = để so sánh hai số.
Bài 5: Để giải bài toán về đơn vị đo độ dài, khối lượng, thời gian, các em cần đổi các đơn vị về cùng một đơn vị trước khi thực hiện phép tính.
Ví dụ 1: Tính 1234 + 5678
Giải:
1234 + 5678 = 6912
Ví dụ 2: Một cửa hàng có 250 kg gạo. Buổi sáng cửa hàng bán được 120 kg gạo, buổi chiều bán được 80 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo cửa hàng bán được trong một ngày là: 120 + 80 = 200 (kg)
Số gạo còn lại là: 250 - 200 = 50 (kg)
Đáp số: 50 kg
Để củng cố kiến thức đã học, các em có thể tự giải thêm các bài tập tương tự trong sách giáo khoa hoặc trên các trang web học toán online.
Bài tập 1: Tính 9876 - 4321
Bài tập 2: Một người nông dân thu hoạch được 300 kg rau. Người đó bán được 200 kg rau với giá 10.000 đồng/kg. Hỏi người nông dân thu được bao nhiêu tiền?
Bài tập 3: Tìm x: x + 123 = 456
Bài tập 4: So sánh 1234 và 4321
Bài tập 5: Đổi 2 km ra mét.
Chúc các em học tốt môn Toán!