Trong chương trình học toán, đặc biệt là phần lượng giác, việc nắm vững bảng giá trị lượng giác của các góc đặc biệt là vô cùng quan trọng. Bảng giá trị lượng giác này giúp giải quyết nhanh chóng các bài toán liên quan đến sin, cos, tan, cot của các góc 0°, 30°, 45°, 60°, 90°.
Tại giaitoan.edu.vn, chúng tôi cung cấp bảng giá trị lượng giác đầy đủ, chính xác và dễ hiểu, hỗ trợ bạn học toán online hiệu quả.
Bảng giá trị lượng giác của các góc đặc biệt Gồm: \({0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ },{120^ \circ },{135^ \circ },{150^ \circ },{180^ \circ }\)
1. Lý thuyết
+ Các góc đặc biệt
Gồm: \({0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ },{120^ \circ },{135^ \circ },{150^ \circ },{180^ \circ }\)
+ Bảng giá trị lượng giác của các góc đặc biệt
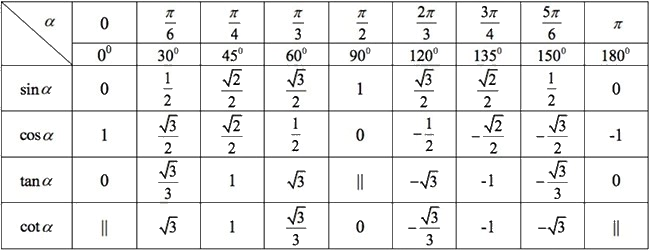
Kí hiệu “||” để chỉ giá trị lượng giác không xác định.
2. Ví dụ minh họa
Ví dụ 1. Tính \(A = \cos {60^ \circ } + \cot {135^ \circ } + \sin {150^ \circ }\); \(B = 2\cos \frac{\pi }{6} + 3\tan \frac{{5\pi }}{6} + \cot \frac{{3\pi }}{4}\)
Sử dụng bảng giá trị lượng giác, ta được:
\(A = \frac{1}{2} + ( - 1) + \frac{1}{2} = 0\)
\(B = 2.\frac{{\sqrt 3 }}{2} + 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + ( - 1) = \sqrt 3 - \sqrt 3 - 1 = - 1.\)
Ví dụ 2. Tìm góc \(\alpha ({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau
a) \(\sin \alpha = \frac{1}{2}\) b) \(\cos \alpha = \frac{{\sqrt 2 }}{2}\) c) \(\tan \alpha = 0\) d) \(\cot \alpha \) không xác định.
Sử dụng bảng giá trị lượng giác, ta được:
a) \(\alpha = {30^ \circ }\) hoặc \(\alpha = {150^ \circ }\)
b) \(\alpha = {45^ \circ }\)
c) \(\alpha = {0^ \circ }\) hoặc \(\alpha = {180^ \circ }\)
d) \(\alpha = {0^ \circ }\) hoặc \(\alpha = {180^ \circ }\)
Lượng giác là một nhánh quan trọng của toán học, nghiên cứu về mối quan hệ giữa các góc và cạnh của tam giác vuông. Các hàm lượng giác cơ bản bao gồm sin, cos, tan, cot, sec và cosec. Trong đó, sin, cos, tan là ba hàm lượng giác được sử dụng phổ biến nhất. Việc hiểu rõ giá trị của các hàm lượng giác tại các góc đặc biệt là nền tảng để giải quyết nhiều bài toán trong toán học và các lĩnh vực ứng dụng khác.
Các góc đặc biệt thường gặp trong lượng giác bao gồm 0°, 30°, 45°, 60° và 90°. Dưới đây là bảng tổng hợp giá trị lượng giác của các góc này:
| Góc (°) | Góc (rad) | sin | cos | tan | cot |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | Không xác định |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | π/2 | 1 | 0 | Không xác định | 0 |
Có nhiều phương pháp để ghi nhớ bảng giá trị lượng giác góc đặc biệt. Một trong những cách phổ biến nhất là sử dụng hình vuông và đường chéo. Hãy tưởng tượng một tam giác vuông cân có cạnh góc vuông bằng 1. Đường chéo của tam giác này sẽ có độ dài là √2. Từ đó, bạn có thể dễ dàng suy ra giá trị sin, cos, tan của góc 45°.
Bảng giá trị lượng giác góc đặc biệt có rất nhiều ứng dụng trong toán học và các lĩnh vực khác:
Ngoài các góc đặc biệt đã nêu trên, bạn cũng có thể sử dụng các công thức lượng giác để tính giá trị lượng giác của các góc lớn hơn. Ví dụ, sin(x + 360°) = sin(x), cos(x + 360°) = cos(x), tan(x + 180°) = tan(x). Việc hiểu rõ các tính chất này giúp bạn mở rộng kiến thức về lượng giác và giải quyết các bài toán phức tạp hơn.
Để nắm vững bảng giá trị lượng giác góc đặc biệt, bạn cần luyện tập thường xuyên. Hãy giải các bài tập liên quan đến lượng giác, sử dụng bảng giá trị lượng giác để kiểm tra kết quả. giaitoan.edu.vn cung cấp nhiều bài tập lượng giác đa dạng, giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán.
Bảng giá trị lượng giác của các góc đặc biệt là một công cụ quan trọng trong học toán. Việc nắm vững bảng này giúp bạn giải quyết nhanh chóng và chính xác các bài toán lượng giác. Hãy dành thời gian để học thuộc và luyện tập, bạn sẽ thấy lượng giác trở nên dễ dàng và thú vị hơn. Chúc bạn học tập tốt tại giaitoan.edu.vn!