Bất phương trình bậc nhất hai ẩn là một phần quan trọng trong chương trình toán học lớp 10. Việc hiểu rõ cách tìm nghiệm và biểu diễn miền nghiệm của bất phương trình này là nền tảng để giải quyết các bài toán phức tạp hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp bạn nắm vững kiến thức về chủ đề này.
Cặp số \(({x_0};{y_0})\) thỏa mãn \(a{x_0} + b{y_0} \le c\) được gọi là một nghiệm của bất phương trình \(ax + by \le c\).
1. Lý thuyết
+ Định nghĩa:
Cặp số \(({x_0};{y_0})\) thỏa mãn \(a{x_0} + b{y_0} \le c\) được gọi là một nghiệm của bất phương trình \(ax + by \le c\).
Nghiệm của các bất phương trình\(ax + by < c;ax + by > c;ax + by \ge c\) được định nghĩa tương tự.
Trong mặt phẳng tọa độ \(Oxy\), miền nghiệm của bất phương trình \(ax + by \le c\) là tập hợp các điểm \(({x_0};{y_0})\) sao cho \(a{x_0} + b{y_0} \le c\).
+ Nhận xét
Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
+ Biểu diễn miền nghiệm của bất phương trình \(ax + by \le c\)
Bước 1: Vẽ đường thẳng \(\Delta :ax + by = c\)
Bước 2: Lấy điểm \(A({x_0};{y_0})\) không thuộc \(\Delta \). Tính \(a{x_0} + b{y_0}\) rồi so sánh với c.
Bước 3: Kết luận
Nếu \(a{x_0} + b{y_0} < c\) thì miền nghiệm là nửa mặt phẳng (kể cả bờ \(\Delta \)) chứa điểm \(A({x_0};{y_0})\).
Nếu \(a{x_0} + b{y_0} > c\) thì miền nghiệm là nửa mặt phẳng (kể cả bờ \(\Delta \)) không chứa điểm \(A({x_0};{y_0})\).
Chú ý: Đường thẳng \(\Delta :ax + by = c\) là tập hợp các điểm (x;y) thỏa mãn \(ax + by = c\).
Do đó miền nghiệm của các bất phương trình \(ax + by < c;ax + by > c\) không chứa đường thẳng \(\Delta \) (hay không kể bờ \(\Delta \)), khi đó ta thường vẽ \(\Delta \) bằng nét đứt.
2. Ví dụ minh họa
+ Nghiệm của bất phương trình bậc nhất hai ẩn:
Cặp số \((2; - 1)\) là một nghiệm của bất phương trình \(3x + 2y \ge - 5\), vì \(3.2 + 2.( - 1) = 4 \ge - 5\)
Cặp số \(( - 2;0)\) không là một nghiệm của bất phương trình \(3x + 2y \ge - 5\), vì \(3.( - 2) + 2.0 = - 6 < - 5\)
+ Biểu diễn miền nghiệm của bất phương trình \(2x - y > 2\)
Bước 1: Vẽ đường thẳng \(\Delta :2x - y = 2\) (nét đứt) đi qua (1;0) và (0; -2).
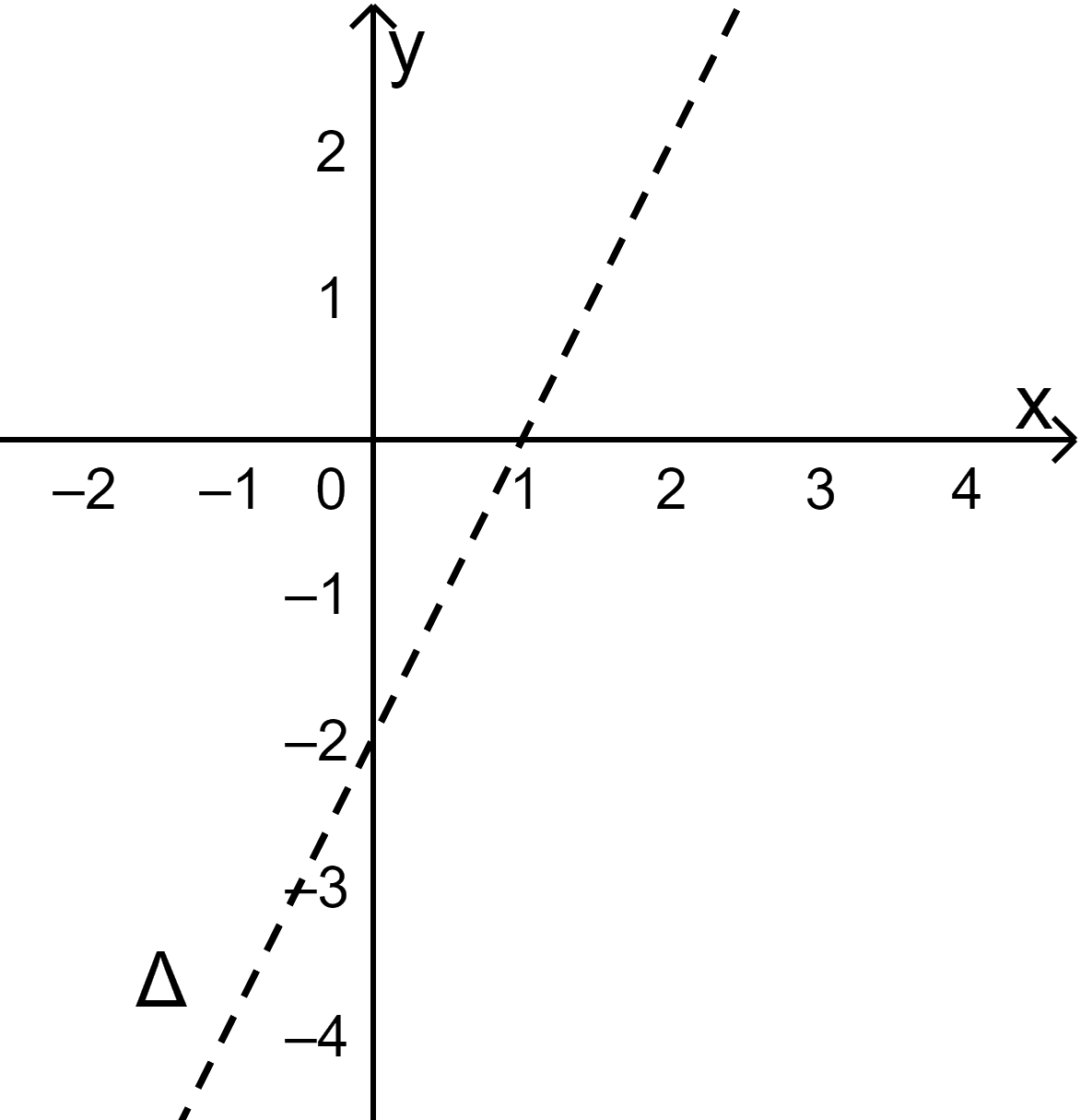
Bước 2: Lấy điểm \(O(0;0)\) không thuộc \(\Delta \). Ta có \(2.0 - 0 = 0\) và \(c = 2\).
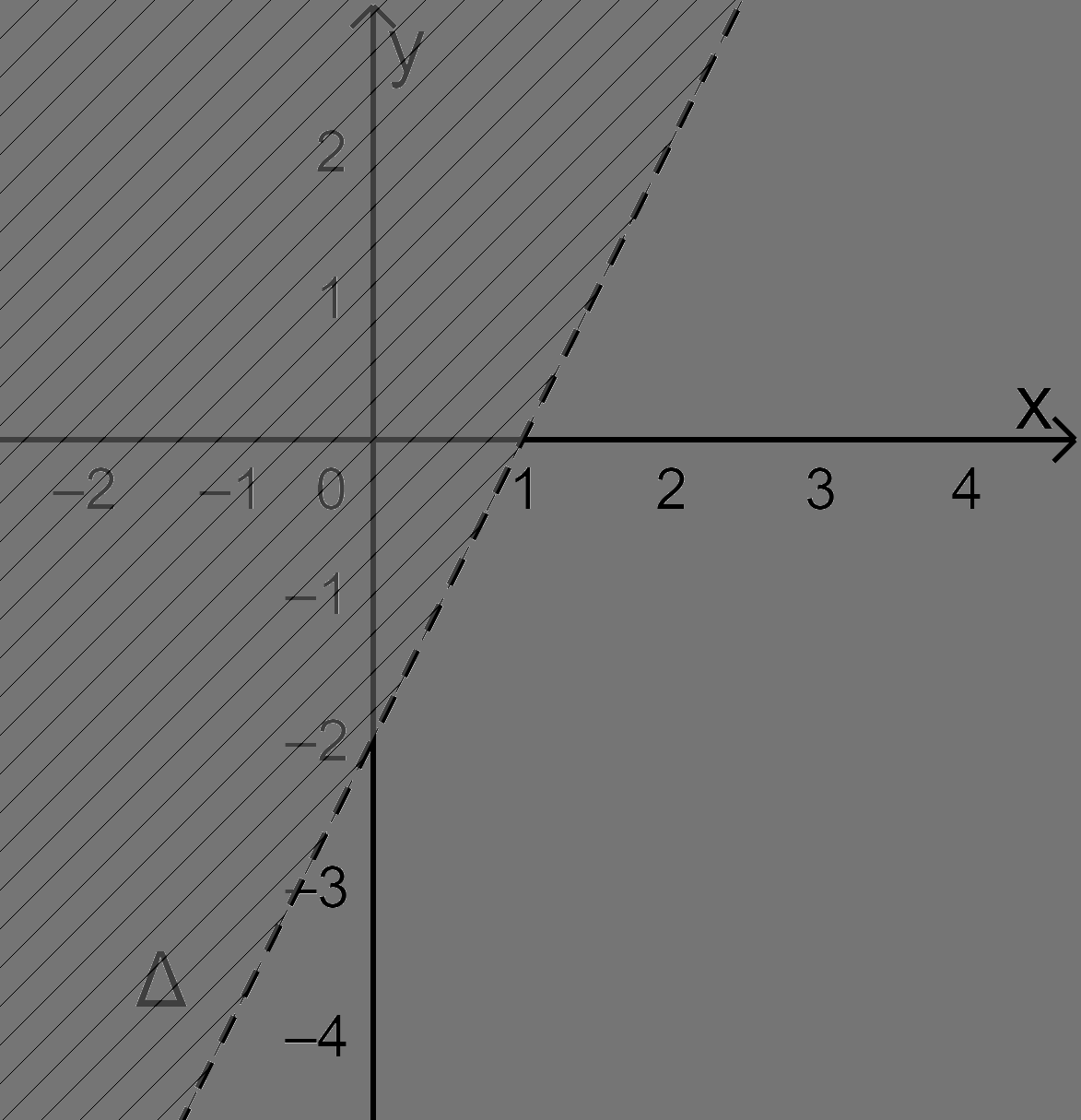
Bước 3: Vì \(2.0 - 0 = 0 < 2\) nên điểm \(O(0;0)\) không thuộc miền nghiệm.
Vậy miền nghiệm là nửa mặt phẳng (không kể bờ \(\Delta \)) không chứa điểm \(O(0;0)\) (miền không gạch chéo).
Bất phương trình bậc nhất hai ẩn là một công cụ quan trọng trong toán học, đặc biệt trong các lĩnh vực như tối ưu hóa tuyến tính và hình học giải tích. Hiểu rõ về nghiệm và miền nghiệm của bất phương trình này là điều cần thiết để giải quyết nhiều bài toán thực tế.
Bất phương trình bậc nhất hai ẩn có dạng tổng quát: ax + by < c (hoặc ax + by ≤ c, ax + by > c, ax + by ≥ c), trong đó a, b, và c là các số thực, và x, y là các ẩn số.
Nghiệm của bất phương trình bậc nhất hai ẩn là các cặp số (x0, y0) sao cho khi thay x = x0 và y = y0 vào bất phương trình, bất phương trình được nghiệm đúng.
Ví dụ: Xét bất phương trình 2x + y ≤ 4. Cặp số (1, 2) là một nghiệm của bất phương trình vì 2(1) + 2 = 4 ≤ 4.
Miền nghiệm của bất phương trình bậc nhất hai ẩn là tập hợp tất cả các điểm (x, y) trên mặt phẳng tọa độ thỏa mãn bất phương trình. Để biểu diễn miền nghiệm, ta thực hiện các bước sau:
Hệ bất phương trình bậc nhất hai ẩn là tập hợp các bất phương trình bậc nhất hai ẩn. Miền nghiệm của hệ là giao của các miền nghiệm của từng bất phương trình trong hệ.
Bất phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, bao gồm:
Bài tập 1: Tìm nghiệm và biểu diễn miền nghiệm của bất phương trình 3x + 2y ≤ 6.
Giải:
Bài tập 2: Tìm miền nghiệm của hệ bất phương trình sau:
| Bất phương trình |
|---|
| x + y ≤ 5 |
| x - y ≥ 1 |
| x ≥ 0 |
| y ≥ 0 |
Việc nắm vững kiến thức về nghiệm và miền nghiệm của bất phương trình bậc nhất hai ẩn là rất quan trọng. Hãy luyện tập thường xuyên để củng cố kiến thức và áp dụng vào giải quyết các bài toán thực tế.