Đồ thị của hàm số

Đồ thị của hàm số - Nền tảng vững chắc cho học sinh, sinh viên

Đồ thị hàm số là một khái niệm quan trọng trong chương trình Toán học, đặc biệt là ở cấp THPT và Đại học. Việc hiểu rõ về đồ thị hàm số không chỉ giúp học sinh, sinh viên nắm vững kiến thức lý thuyết mà còn ứng dụng vào giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập hiệu quả về đồ thị hàm số, giúp bạn học tập một cách dễ dàng và hiệu quả nhất.

Đồ thị của hàm số \(y = f(x)\) xác định trên tập D là tập hợp tất cả các điểm \(M(x;f(x))\) trên mặt phẳn tọa độ với mọi x thuộc D. Kí hiệu: \((C) = \{ M(x;f(x))|x \in D\} \)

1. Lý thuyết

+ Định nghĩa:

Đồ thị của hàm số \(y = f(x)\) xác định trên tập D là tập hợp tất cả các điểm \(M(x;f(x))\) trên mặt phẳn tọa độ với mọi x thuộc D.

Kí hiệu: \((C) = \{ M(x;f(x))|x \in D\} \)

+ Kiểm tra điểm thuộc đồ thị hàm số

Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\)

Điểm \(M({x_M};{y_M})\) không thuộc đồ thị hàm số \(y = f(x)\)\( \Leftrightarrow \left[ \begin{array}{l}{x_M} \notin D\\{y_M} \ne f({x_M})\end{array} \right.\)

2. Ví dụ minh họa

Đồ thị hàm số \(y = 2x - 3\)

\((C) = \{ M(x;2x - 3)|x \in \mathbb{R}\} \)

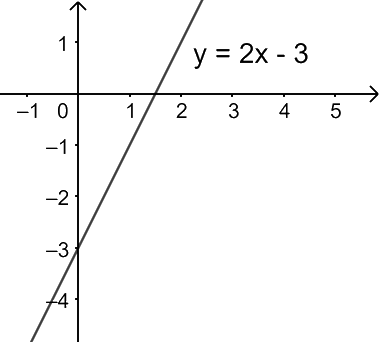
Đồ thị của hàm số 1

Đồ thị hàm số \(y = 2x - 3\) là đường thẳng, đi qua hai điểm (0;-3) và (1,5;0).

Điểm thuộc đồ thị hàm số, điểm không thuộc đồ thị hàm số

Quan sát đồ thị của hàm số \(y = {x^2} - 4\)

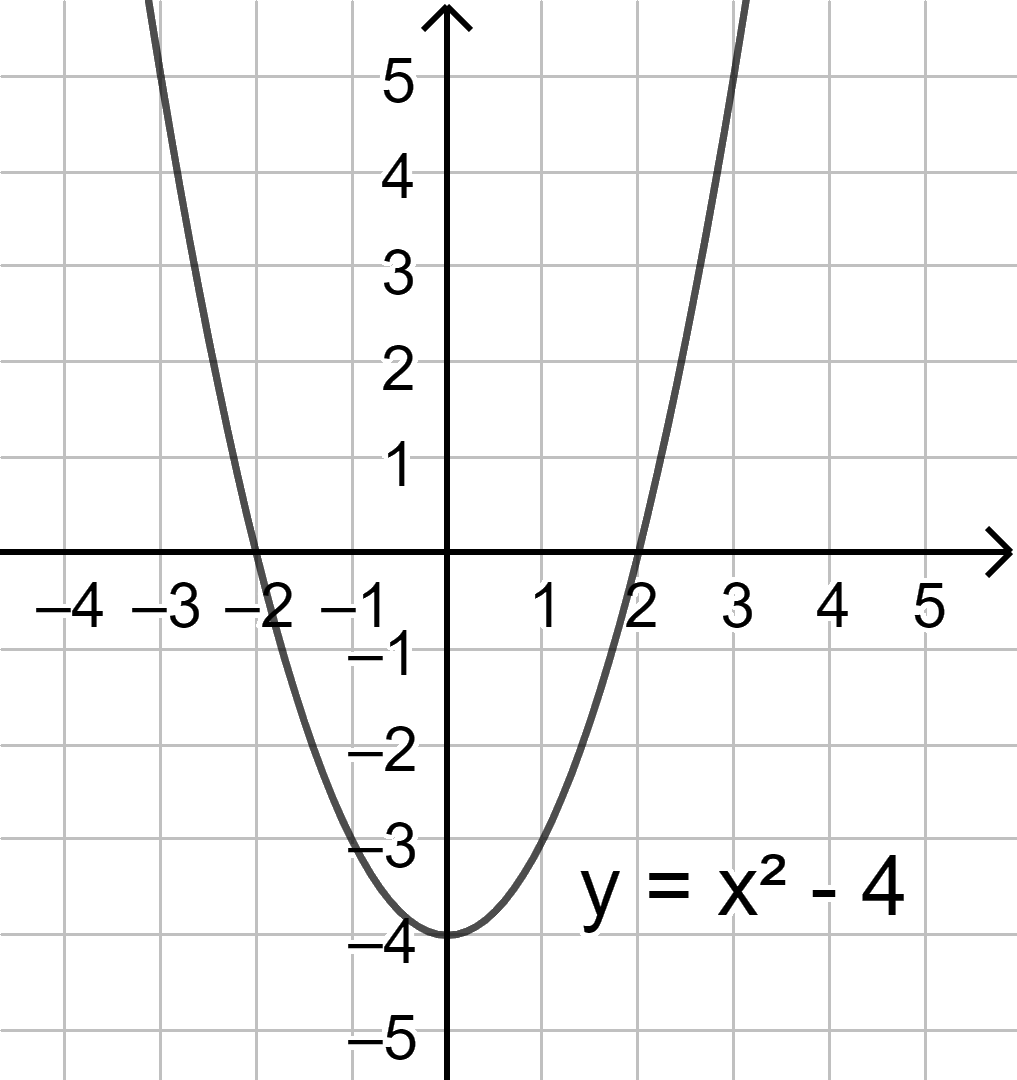
Đồ thị của hàm số 2

Các điểm (2;0), (-2;0), (1; -3), (0;-4) thuộc đồ thị hàm số.

Các điểm (2;2), (-2;3), (1; 2), (0;3) không thuộc đồ thị hàm số.

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Đồ thị của hàm số đặc sắc thuộc chuyên mục giải sgk toán 10 trên nền tảng toán học. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Đồ thị của hàm số: Tổng quan và các khái niệm cơ bản

Đồ thị của một hàm số f(x) là tập hợp tất cả các điểm (x, y) trên mặt phẳng tọa độ, sao cho y = f(x). Nói cách khác, đồ thị hàm số là hình ảnh trực quan biểu diễn mối quan hệ giữa biến độc lập x và biến phụ thuộc y.

Để hiểu rõ hơn về đồ thị hàm số, chúng ta cần nắm vững các khái niệm sau:

Miền xác định: Tập hợp tất cả các giá trị của x mà hàm số f(x) có nghĩa.
Tập giá trị: Tập hợp tất cả các giá trị của y mà hàm số f(x) có thể nhận được.
Điểm thuộc đồ thị: Một điểm (x₀, y₀) được gọi là điểm thuộc đồ thị của hàm số f(x) nếu y₀ = f(x₀).
Tính đối xứng: Đồ thị hàm số có thể đối xứng qua trục hoành, trục tung hoặc gốc tọa độ.
Tính đơn điệu: Hàm số được gọi là đơn điệu nếu nó luôn tăng hoặc luôn giảm trên một khoảng nào đó.

Các loại đồ thị hàm số phổ biến

Có rất nhiều loại đồ thị hàm số khác nhau, tùy thuộc vào dạng hàm số. Dưới đây là một số loại đồ thị hàm số phổ biến:

Đồ thị hàm số bậc nhất: y = ax + b (a ≠ 0) là một đường thẳng.
Đồ thị hàm số bậc hai: y = ax² + bx + c (a ≠ 0) là một parabol.
Đồ thị hàm số mũ: y = a^x (a > 0, a ≠ 1) có dạng đường cong luôn đi qua điểm (0, 1).
Đồ thị hàm số logarit: y = log_ax (a > 0, a ≠ 1) có dạng đường cong luôn đi qua điểm (1, 0).
Đồ thị hàm số lượng giác: Các hàm số sin, cos, tan, cot có đồ thị là các đường cong tuần hoàn.

Cách vẽ đồ thị hàm số

Để vẽ đồ thị hàm số, chúng ta có thể thực hiện các bước sau:

Xác định miền xác định của hàm số.
Tính các điểm đặc biệt của hàm số: Điểm giao với trục hoành, trục tung, điểm cực trị, điểm uốn,...
Lập bảng biến thiên của hàm số.
Vẽ đồ thị hàm số dựa trên các thông tin đã thu thập.

Ứng dụng của đồ thị hàm số

Đồ thị hàm số có rất nhiều ứng dụng trong thực tế, bao gồm:

Giải các bài toán tìm nghiệm của phương trình, bất phương trình.
Nghiên cứu sự biến thiên của hàm số.
Dự đoán giá trị của hàm số tại một điểm nào đó.
Mô tả các hiện tượng vật lý, kinh tế, xã hội.

Bài tập luyện tập về đồ thị hàm số

Để củng cố kiến thức về đồ thị hàm số, bạn có thể luyện tập với các bài tập sau:

Bài tập	Đáp án
Vẽ đồ thị hàm số y = 2x + 1	Đường thẳng đi qua các điểm (-1, -1) và (0, 1)
Tìm tập giá trị của hàm số y = x² - 4x + 3	[ -1, +∞ )
Xác định tính đơn điệu của hàm số y = log₂x	Hàm số đồng biến trên (0, +∞)

Kết luận

Đồ thị hàm số là một công cụ quan trọng trong việc nghiên cứu và ứng dụng Toán học. Hy vọng rằng, với những kiến thức và bài tập luyện tập được cung cấp trong bài viết này, bạn sẽ nắm vững kiến thức về đồ thị hàm số và có thể áp dụng chúng vào giải quyết các bài toán thực tế.