Hàm số bậc hai là một trong những chủ đề quan trọng trong chương trình toán học cấp trung học phổ thông. Việc nắm vững kiến thức về hàm số bậc hai và đồ thị của nó không chỉ giúp học sinh giải quyết các bài toán đại số mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, giúp bạn tự tin chinh phục chủ đề này.
Hàm số bậc hai là hàm số cho bởi công thức \(y = a{x^2} + bx + c\), trong đó \(x\) là biến số, \(a,b,c\) là hằng số và \(a \ne 0\).
1. Lý thuyết
+ Định nghĩa:
Hàm số bậc hai là hàm số cho bởi công thức \(y = a{x^2} + bx + c\), trong đó \(x\) là biến số, \(a,b,c\) là hằng số và \(a \ne 0\).
Tập xác định của hàm số bậc hai là \(\mathbb{R}\)
+ Đồ thị hàm số bậc hai
Đồ thị hàm số \(y = a{x^2} + bx + c\;(a \ne 0)\) là một parabol, có đỉnh là điểm \(I\left( { - \frac{b}{{2a}}; - \frac{{{b^2} - 4ac}}{{4a}}} \right)\), có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}}\).
Parabol này quay bề lõm lên trên nếu \(a > 0\), xuống dưới nếu \(a < 0\).
+ Các bước vẽ đồ thị hàm số \(y = a{x^2} + bx + c\)
Bước 1: Xác định a,b,c từ đó suy ra tọa độ đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{{{b^2} - 4ac}}{{4a}}} \right)\)
Bước 2: Xác định trục đối xứng \(x = - \frac{b}{{2a}}\)
Bước 3: Xác định giao điểm của parabol với trục tung, trục hoành (nếu có) và vài điểm đặc biệt (đối xứng nhau qua trục đối xứng) trên parabol
Bước 4: Vẽ parabol.
2. Ví dụ minh họa
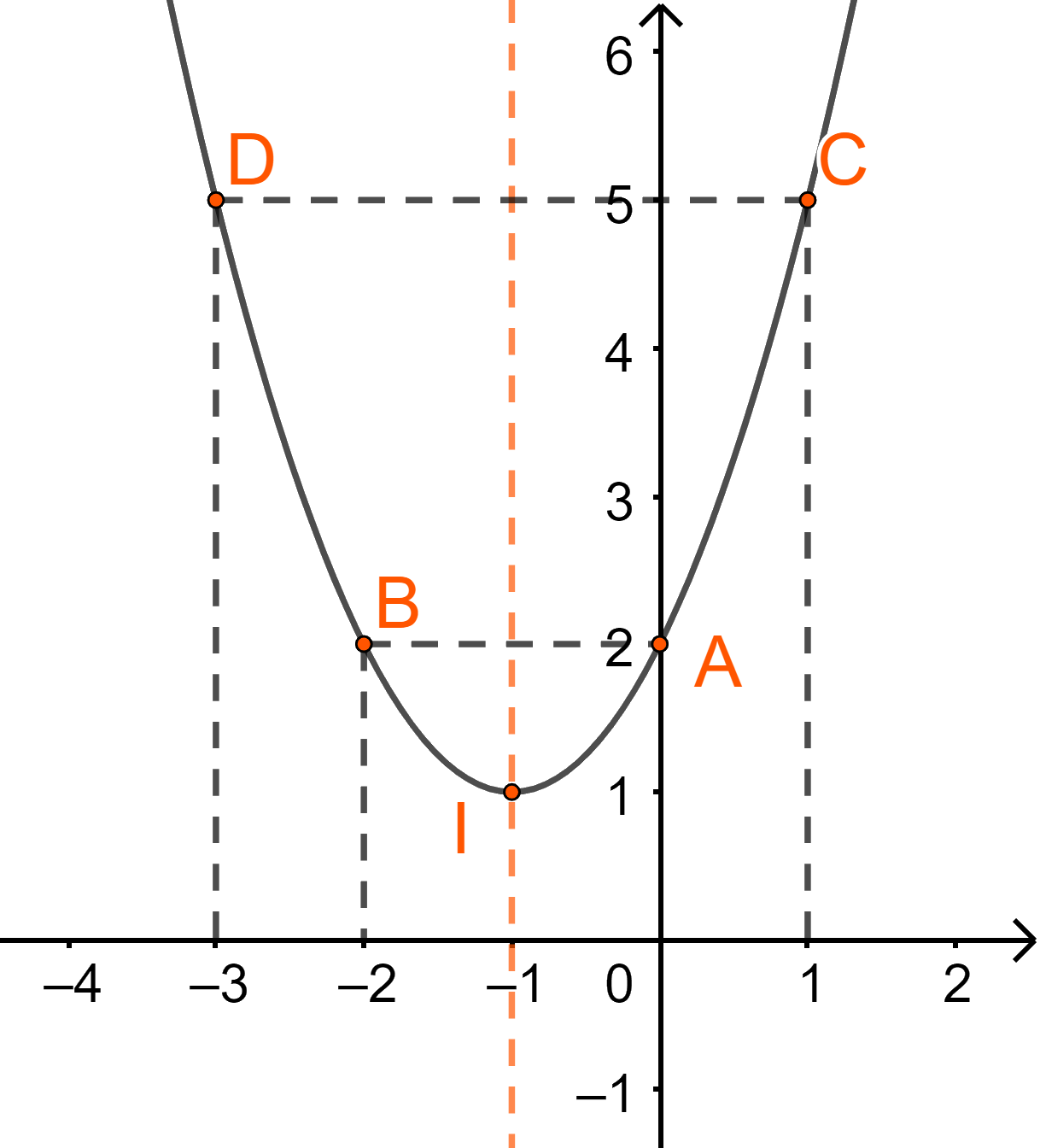
Ví dụ 1.Vẽ đồ thị hàm số \(y = {x^2} + 2x + 2\)
Hàm số \(y = {x^2} + 2x + 2\) có \(a = 1,b = 2,c = 2\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{2}{{2.1}} = - 1;y( - 1) = {( - 1)^2} + 2.( - 1) + 2 = 1\)
+ Tọa độ đỉnh \(I( - 1;1)\)
+ Trục đối xứng \(x = - 1\)
+ Giao điểm với trục tung là A(0;2), không cắt trục hoành (vì \(y = {x^2} + 2x + 2 = {(x + 1)^2} + 1 > 0\;\forall x \in \mathbb{R}\))
+ Lấy điểm B(-2;2) đối xứng với A(0;2) qua trục đối xứng. Điểm C(1;5), D(-3;5) thuộc đồ thị.
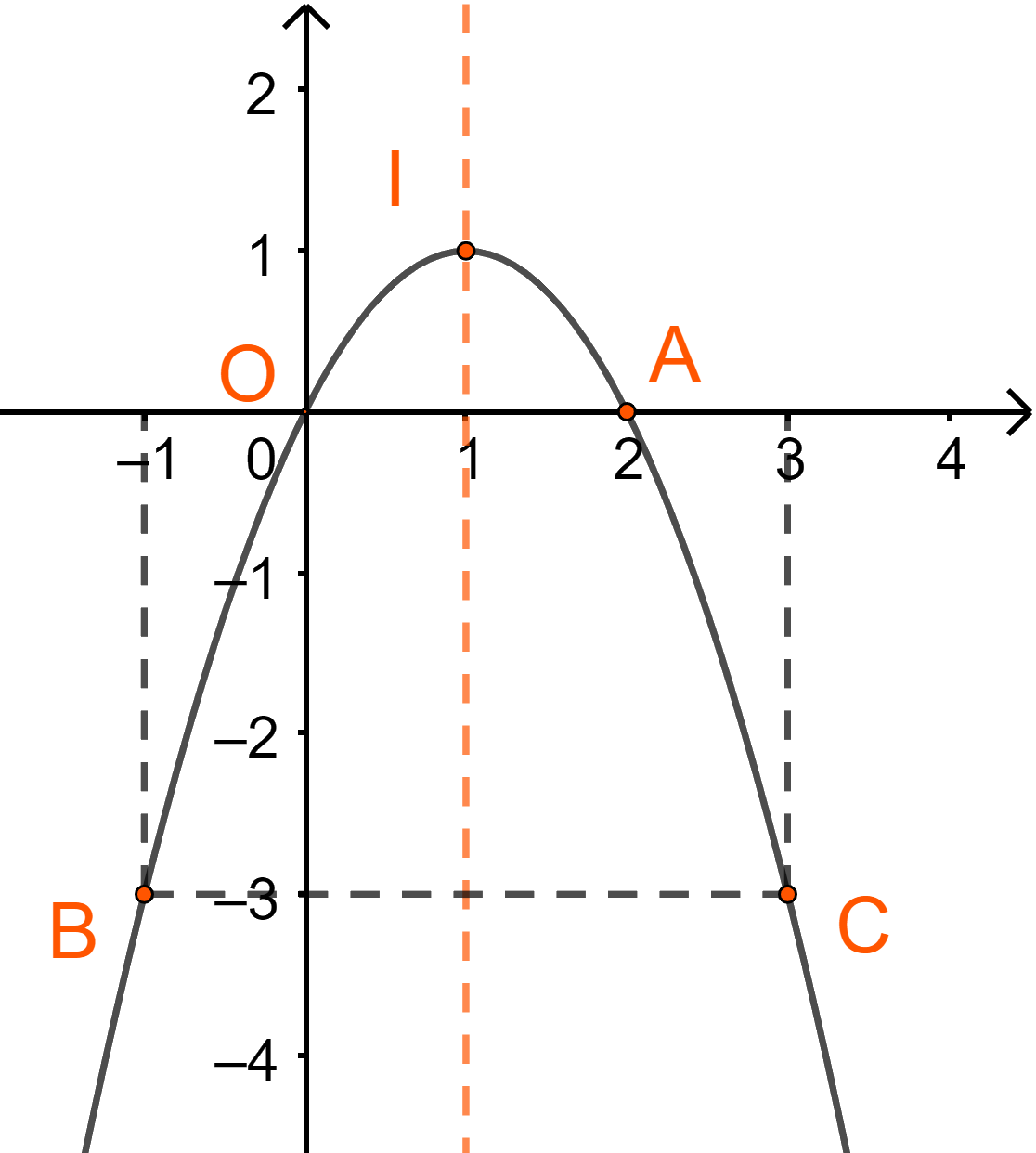
Ví dụ 2.Vẽ đồ thị hàm số \(y = - {x^2} + 2x\)
Hàm số \(y = - {x^2} + 2x\) có \(a = - 1,b = 2,c = 0\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1;y(1) = - {1^2} + 2.1 = 1\)
+ Tọa độ đỉnh \(I(1;1)\)
+ Trục đối xứng \(x = 1\)
+ Giao điểm với trục tung là O(0;0), điểm giao với trục hoành là A(2;0)
+ Lấy điểm B(-1;-3) thuộc đồ thị. Điểm C(3;-3) đối xứng với B(-1;-3) qua trục đối xứng
Hàm số bậc hai là hàm số có dạng y = ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0. Hàm số bậc hai có nhiều ứng dụng trong thực tế, từ việc mô tả quỹ đạo của vật thể ném lên đến việc tối ưu hóa các bài toán kinh tế.
Hệ số a quyết định độ lồi hoặc lõm của parabol. Nếu a > 0, parabol hướng lên trên (lõm xuống). Nếu a < 0, parabol hướng xuống dưới (lồi lên). Hệ số b ảnh hưởng đến vị trí đỉnh của parabol. Hệ số c là giao điểm của parabol với trục tung (trục Oy).
Nghiệm của hàm số bậc hai là các giá trị của x sao cho y = 0. Để tìm nghiệm, ta giải phương trình bậc hai ax² + bx + c = 0. Phương pháp giải phổ biến là sử dụng công thức nghiệm:
x = (-b ± √(b² - 4ac)) / 2a
Biệt thức Δ = b² - 4ac quyết định số nghiệm của phương trình:
Đồ thị của hàm số bậc hai là một đường cong hình parabol. Parabol có những đặc điểm quan trọng sau:
Đỉnh của parabol là điểm thấp nhất (nếu a > 0) hoặc điểm cao nhất (nếu a < 0) trên đồ thị. Tọa độ đỉnh của parabol là:
I(x₀; y₀), với x₀ = -b / 2a và y₀ = f(x₀)
Trục đối xứng của parabol là đường thẳng đi qua đỉnh và song song với trục Oy. Phương trình của trục đối xứng là:
x = -b / 2a
Giao điểm của parabol với trục tung là điểm có tọa độ (0; c).
Giao điểm của parabol với trục hoành là các nghiệm của phương trình bậc hai ax² + bx + c = 0.
Hàm số bậc hai được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
Để củng cố kiến thức, hãy thực hành giải các bài tập sau:
| Bài tập | Nội dung |
|---|---|
| 1 | Tìm nghiệm của phương trình x² - 5x + 6 = 0. |
| 2 | Xác định tọa độ đỉnh của parabol y = 2x² + 4x - 1. |
| 3 | Vẽ đồ thị hàm số y = -x² + 2x + 3. |
Hy vọng với những kiến thức và bài tập trên, bạn đã có cái nhìn tổng quan và hiểu rõ hơn về hàm số bậc hai và đồ thị của nó. Hãy luyện tập thường xuyên để nắm vững kiến thức này nhé!