Hàm số bậc hai là một trong những khái niệm cơ bản và quan trọng trong chương trình Toán học, đặc biệt là ở cấp THPT. Việc hiểu rõ sự biến thiên của hàm số bậc hai giúp học sinh giải quyết nhiều bài toán thực tế và xây dựng nền tảng vững chắc cho các kiến thức nâng cao.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về sự biến thiên của hàm số bậc hai, kèm theo các ví dụ minh họa và bài tập luyện tập đa dạng.
(a > 0) Hàm số nghịch biến trên (( - infty ; - frac{b}{{2a}})), đồng biến trên (( - frac{b}{{2a}}; + infty ))
1. Lý thuyết
Cho hàm số \(y = a{x^2} + bx + c\;(a \ne 0)\)
Trên khoảng \(( - \infty ; - \frac{b}{{2a}})\) | Trên khoảng \(( - \frac{b}{{2a}}; + \infty )\) | |
\(a > 0\) | Hàm số nghịch biến | Hàm số đồng biến |
\(a < 0\) | Hàm số đồng biến | Hàm số nghịch biến |
+ Bảng biến thiên
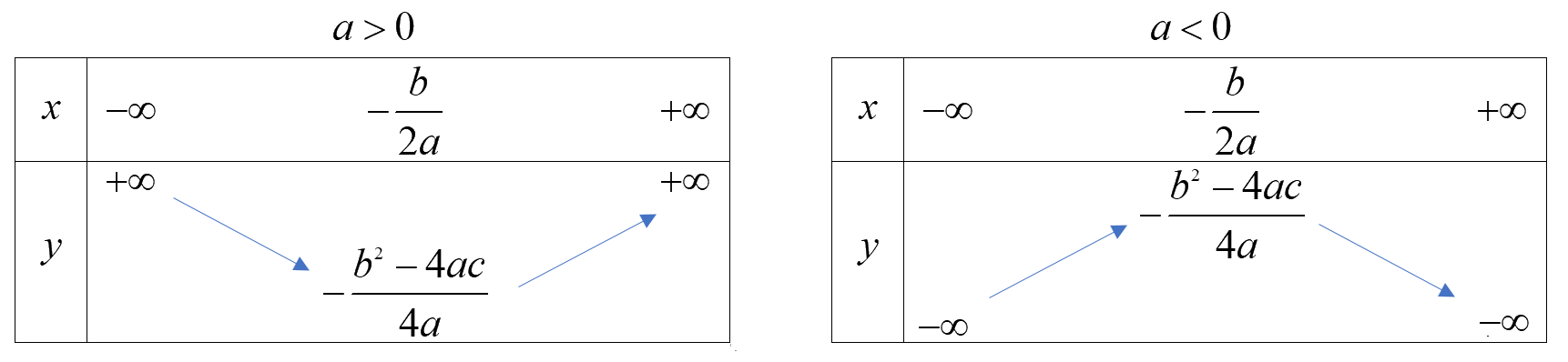
+ Chú ý
Từ bảng biến thiên, ta thấy
Khi \(a > 0\), hàm số đạt giá trị nhỏ nhất bằng \( - \frac{{{b^2} - 4ac}}{{4a}}\) tại \(x = - \frac{b}{{2a}}\) và hàm số có tập giá trị là \([ - \frac{{{b^2} - 4ac}}{{4a}}; + \infty )\)
Khi \(a < 0\), hàm số đạt giá trị lớn nhất bằng \( - \frac{{{b^2} - 4ac}}{{4a}}\) tại \(x = - \frac{b}{{2a}}\) và hàm số có tập giá trị là \(( - \infty ; - \frac{{{b^2} - 4ac}}{{4a}}]\)
2. Ví dụ minh họa
Ví dụ 1.Xét sự biến thiên của hàm số \(y = {x^2} + 2x + 2\)
Hàm số \(y = {x^2} + 2x + 2\) có \(a = 1,b = 2,c = 2\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{2}{{2.1}} = - 1;y( - 1) = {( - 1)^2} + 2.( - 1) + 2 = 1\)
Bảng biến thiên
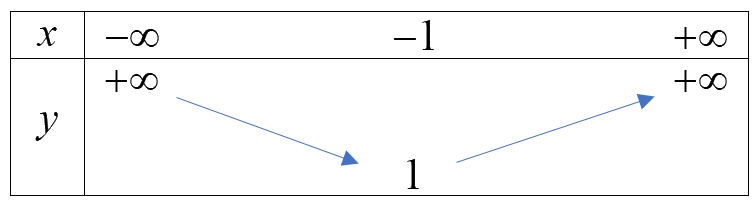
Hàm số đồng biến trên \(( - 1; + \infty )\), nghịch biến trên \(( - \infty ; - 1)\)
Ví dụ 2.Lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số \(y = - {x^2} + 2x\)
Hàm số \(y = - {x^2} + 2x\) có \(a = - 1,b = 2,c = 0\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1;y(1) = - {1^2} + 2.1 = 1\)
Bảng biến thiên
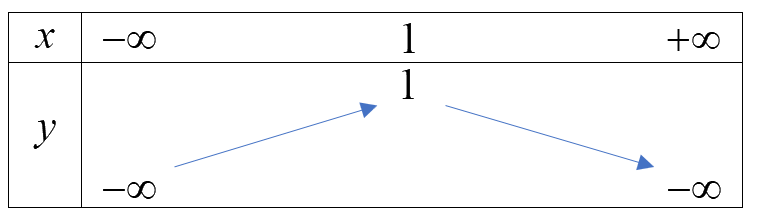
Hàm số đồng biến trên \(( - \infty ;1)\), nghịch biến trên \((1; + \infty )\)
Hàm số bậc hai có dạng tổng quát: y = ax² + bx + c, với a, b, c là các số thực và a ≠ 0. Sự biến thiên của hàm số này được quyết định bởi các yếu tố như hệ số a, đỉnh của parabol, trục đối xứng và các điểm đặc biệt khác.
Hệ số a đóng vai trò quan trọng trong việc xác định chiều biến thiên của parabol:
Đỉnh của parabol là điểm có tọa độ I(x₀, y₀), trong đó:
Đỉnh của parabol là điểm quan trọng để xác định tính chất của hàm số, đặc biệt là giá trị lớn nhất hoặc nhỏ nhất của hàm số.
Trục đối xứng của parabol là đường thẳng có phương trình x = -b/2a. Đường thẳng này đi qua đỉnh của parabol và chia parabol thành hai phần đối xứng nhau.
Bảng biến thiên là một công cụ hữu ích để tóm tắt các thông tin quan trọng về sự biến thiên của hàm số. Dưới đây là ví dụ về bảng biến thiên của hàm số bậc hai:
| x | -∞ | -b/2a | +∞ |
|---|---|---|---|
| y' | + (nếu a > 0) hoặc - (nếu a < 0) | 0 | - (nếu a > 0) hoặc + (nếu a < 0) |
| y | Giảm (nếu a > 0) hoặc Tăng (nếu a < 0) | y₀ (giá trị lớn nhất hoặc nhỏ nhất) | Tăng (nếu a > 0) hoặc Giảm (nếu a < 0) |
Ngoài đỉnh, parabol còn có các điểm đặc biệt khác như:
Kiến thức về sự biến thiên của hàm số bậc hai có nhiều ứng dụng trong thực tế, bao gồm:
Để nắm vững kiến thức về sự biến thiên của hàm số bậc hai, bạn nên luyện tập các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về sự biến thiên của hàm số bậc hai. Hãy truy cập giaitoan.edu.vn để học thêm nhiều kiến thức toán học thú vị khác!