Trong toán học, đặc biệt là trong lý thuyết tập hợp, giao của hai tập hợp là tập hợp chứa tất cả các phần tử chung của cả hai tập hợp đó. Đây là một khái niệm cơ bản và quan trọng, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau của toán học.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu về giao của hai tập hợp, giúp bạn nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.
Tập hợp gồm các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B. Kí hiệu: (A cap B)
1. Lý thuyết
+ Định nghĩa:
Tập hợp gồm các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B.
+ Kí hiệu: \(A \cap B\)
+ Nhận xét
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
\(A \cap B = A \Leftrightarrow A \subset B\)
+ Biểu đồ Ven
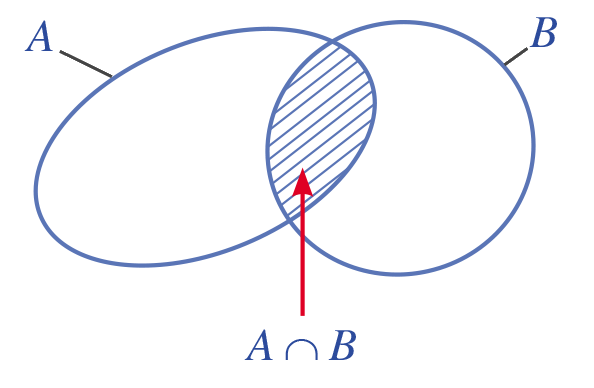
+ Xác định giao của hai tập con của \(\mathbb{R}\)
Bước 1: Biểu diễn hai tập hợp đó trên cùng một trục số.
Bước 2: Phần không bị gạch là tập giao cần tìm.
2. Ví dụ minh họa
Ví dụ 1. Cho tập hợp \(C = \{ 2;3;5;7\} \) và \(D = \{ - 1;2;4;5;9\} \)
Tập hợp \(C \cap D = \{ 2;5\} \)
Ví dụ 2. Cho tập hợp \(A = ( - 3;5]\) và \(B = [1; + \infty )\). Xác định \(A \cap B\) và biểu diễn trên trục số.
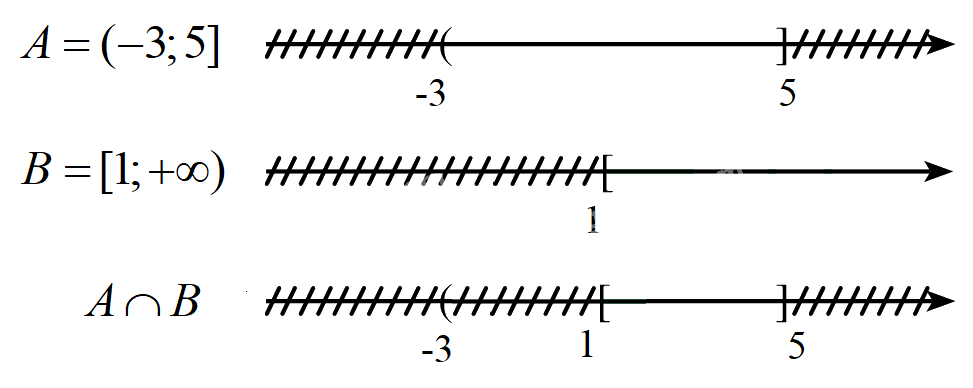
Vậy \(A \cap B = [1;5]\)
Giao của hai tập hợp A và B, ký hiệu là A ∩ B, là tập hợp chứa tất cả các phần tử thuộc cả A và B. Nói cách khác, một phần tử x thuộc A ∩ B khi và chỉ khi x thuộc A và x thuộc B.
Định nghĩa chính thức: A ∩ B = {x | x ∈ A và x ∈ B}
Xét hai tập hợp:
Khi đó, giao của A và B là:
A ∩ B = {3, 5}
Sơ đồ Venn là một công cụ trực quan hữu ích để minh họa các phép toán trên tập hợp, bao gồm cả phép giao. Giao của hai tập hợp A và B được biểu diễn bằng phần diện tích chung của hai vòng tròn đại diện cho A và B.
Giao của hai tập hợp có nhiều ứng dụng trong thực tế, bao gồm:
Dưới đây là một số bài tập để bạn luyện tập về giao của hai tập hợp:
Khái niệm giao của hai tập hợp có thể được mở rộng cho nhiều tập hợp. Giao của n tập hợp A1, A2, ..., An, ký hiệu là A1 ∩ A2 ∩ ... ∩ An, là tập hợp chứa tất cả các phần tử thuộc tất cả các tập hợp A1, A2, ..., An.
Tập hợp bù của A trong tập hợp vũ trụ U, ký hiệu là A', là tập hợp chứa tất cả các phần tử thuộc U nhưng không thuộc A. Mối quan hệ giữa giao của hai tập hợp và tập hợp bù được thể hiện qua các công thức sau:
Giao của hai tập hợp là một khái niệm cơ bản và quan trọng trong lý thuyết tập hợp. Việc nắm vững định nghĩa, tính chất và ứng dụng của phép giao tập hợp là rất cần thiết để giải quyết các bài toán toán học và các vấn đề thực tế. Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về giao của hai tập hợp.