Bài viết này cung cấp kiến thức cơ bản và nâng cao về giá trị lượng giác của các góc từ 0 đến 180 độ. Chúng ta sẽ cùng nhau khám phá các hàm sin, cosin, tang và cotang, cùng với các công thức và ứng dụng quan trọng trong toán học.
Nội dung được trình bày một cách dễ hiểu, kèm theo ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
(sin alpha = {y_0}) là tung độ của M (cos alpha = {x_0}) là hoành độ của M (tan alpha = frac{{sin alpha }}{{cos alpha }} = frac{{{y_0}}}{{{x_0}}}(alpha ne {90^o})) (cot alpha = frac{{cos alpha }}{{sin alpha }} = frac{{{x_0}}}{{{y_0}}}(alpha ne {0^o},alpha ne {180^o}))
1. Lý thuyết
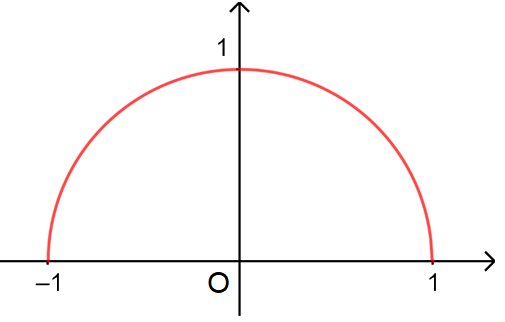
+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành.
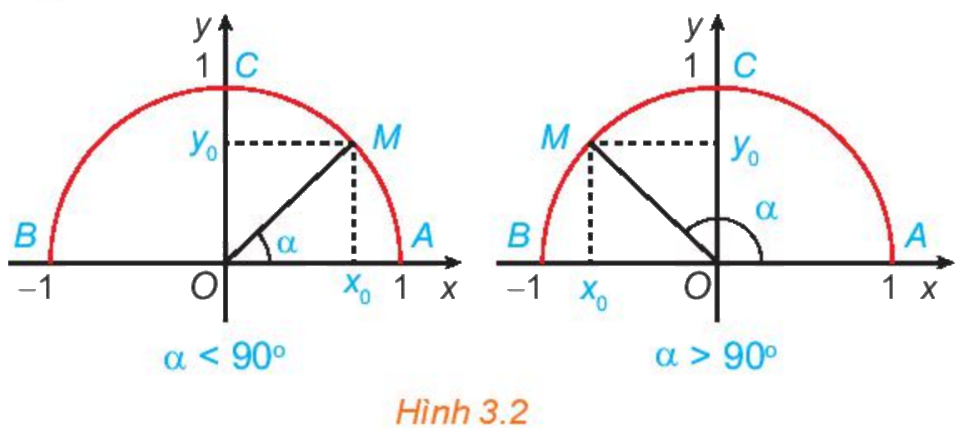
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\)có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\) Khi đó:
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)
+ Nhận xét:
\({0^ \circ } < \alpha < {90^ \circ }:\cos \alpha > 0,\sin \alpha > 0,\tan \alpha > 0,\cot \alpha > 0.\)
\({90^ \circ } < \alpha < {180^ \circ }:\cos \alpha < 0,\sin \alpha > 0,\tan \alpha < 0,\cot \alpha < 0.\)
+ Cách xác định điểm trên nửa đường tròn đơn vị tương ứng với góc \(\alpha \)
Bước 1. Ta đã biết góc \(\alpha \), sử dụng máy tính hoặc các công cụ khác để tìm \(\sin \alpha \) và \(\cos \alpha \).
Bước 2. Xác định M trên hệ trục, với \({x_M} = \cos \alpha \) và \({y_M} = \sin \alpha \)
+ Cách xác định góc tương ứng với điểm trên nửa đường tròn đơn vị.
Ta đã biết điểm M, tức là đã biết hoành độ và tung độ của M, kí hiệu là \({x_M},{y_M}.\)
Bước 1. Đặt \(\alpha = \widehat {xOM}\), là góc cần tìm. Khi đó \({x_M} = \cos \alpha \) và \({y_M} = \sin \alpha \)
Bước 2. Sử dụng máy tính hoặc các công cụ khác để tìm \(\alpha \).
2. Ví dụ minh họa
Ví dụ 1. Tìm các giá trị lượng giác của góc \({63^o}\)
Sử dụng máy tính cầm tay, ta được:
\(\begin{array}{l}\sin {63^o} \approx 0,891\\\cos {63^o} \approx 0,454\\\tan {63^o} \approx 1,963\\\cot {63^o} = 1:\tan {63^o} \approx 0,51\end{array}\)
Ví dụ 2. Tìm góc \(\alpha ({0^o} \le \alpha \le {180^o})\) thỏa mãn \(\sin \alpha = 0,67\)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \({y_M} = 0,67\). Dễ thấy có 2 điểm thỏa mãn, gọi là M và M’.
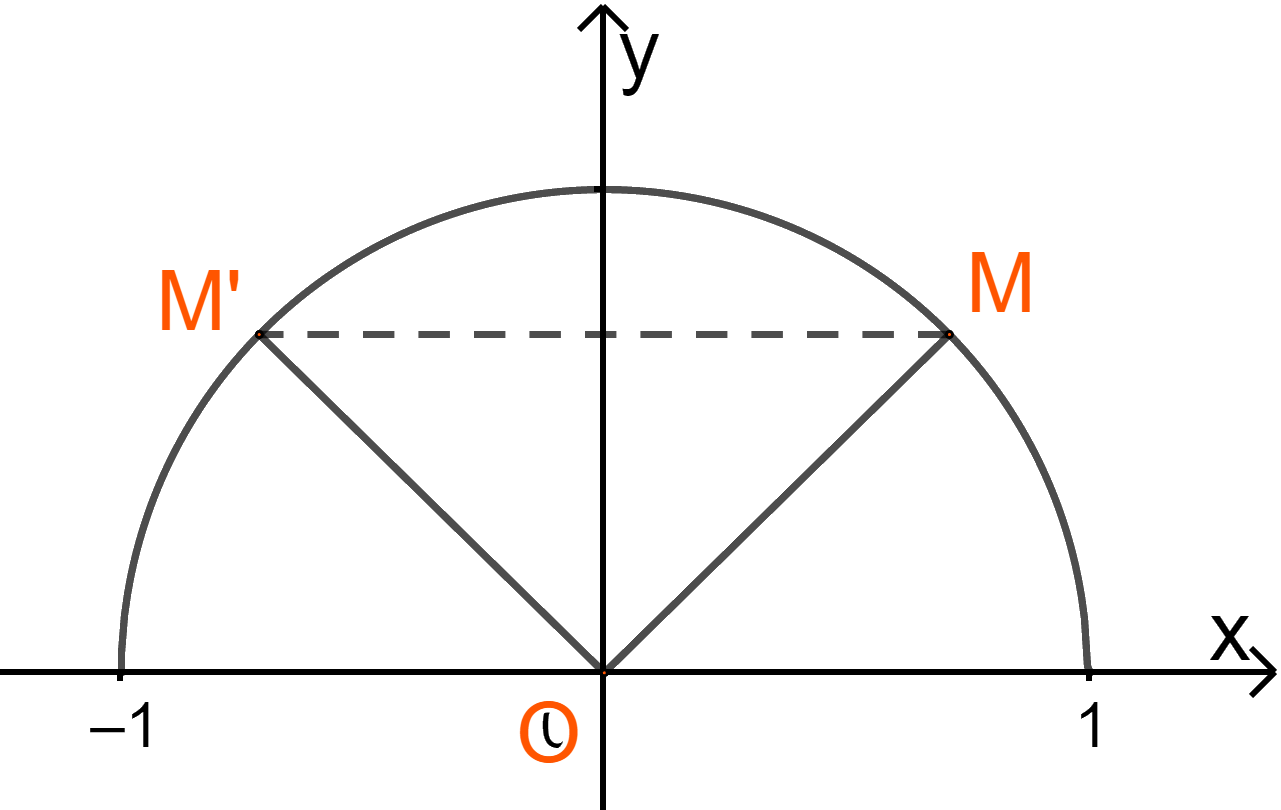
Do đó có hai góc thỏa mãn là \(\widehat {xOM}\) và \(\widehat {xOM'}\), trong đó \(\widehat {xOM} < {90^ \circ } < \widehat {xOM'}\).
Vì M và M’ đối xứng nhau qua Oy nên \(\widehat {MOy} = \widehat {M'Oy}\)\( \Rightarrow \widehat {M'Oy} = {90^ \circ } - \widehat {xOM} \Rightarrow \widehat {xOM'} = {90^ \circ } + \widehat {M'Oy} = {180^ \circ } - \widehat {xOM}\)
Dùng máy tính, bấm SHIFT sin 0.67 =, ta được góc xấp xỉ \({42^o}\)
\( \Rightarrow \widehat {xOM} = {42^ \circ },\widehat {xOM'} = {180^ \circ } - {42^ \circ } = {138^ \circ }\)
Vậy \(\alpha = {42^ \circ }\) hoặc \(\alpha = {138^ \circ }\)
Trong toán học, đặc biệt là trong lĩnh vực lượng giác, việc hiểu rõ giá trị lượng giác của các góc là vô cùng quan trọng. Các giá trị này đóng vai trò then chốt trong việc giải quyết nhiều bài toán liên quan đến tam giác, đường tròn lượng giác và các ứng dụng thực tế khác.
Có bốn hàm lượng giác cơ bản thường được sử dụng:
Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt từ 0 đến 180 độ:
| Góc (độ) | Sin | Cos | Tan | Cot |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | Không xác định |
| 30 | 1/2 | √3/2 | 1/√3 | √3 |
| 45 | √2/2 | √2/2 | 1 | 1 |
| 60 | √3/2 | 1/2 | √3 | 1/√3 |
| 90 | 1 | 0 | Không xác định | 0 |
| 120 | √3/2 | -1/2 | -√3 | -1/√3 |
| 135 | √2/2 | -√2/2 | -1 | -1 |
| 150 | 1/2 | -√3/2 | -1/√3 | -√3 |
| 180 | 0 | -1 | 0 | Không xác định |
Các hàm lượng giác có mối quan hệ mật thiết với nhau, được thể hiện qua các công thức sau:
Giá trị lượng giác có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Ví dụ 1: Tính giá trị của sin(30°) + cos(60°)
sin(30°) = 1/2
cos(60°) = 1/2
sin(30°) + cos(60°) = 1/2 + 1/2 = 1
Ví dụ 2: Cho tam giác ABC vuông tại A, biết AB = 3cm và AC = 4cm. Tính sin(B), cos(B) và tan(B).
BC = √(AB2 + AC2) = √(32 + 42) = 5cm
sin(B) = AC/BC = 4/5
cos(B) = AB/BC = 3/5
tan(B) = AC/AB = 4/3
Việc nắm vững giá trị lượng giác của các góc từ 0 đến 180 độ là nền tảng quan trọng để học tập và làm việc trong nhiều lĩnh vực. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc giải quyết các bài toán liên quan đến lượng giác.