Trong chương trình Toán học, đặc biệt là ở giai đoạn THPT, kiến thức về tập hợp đóng vai trò vô cùng quan trọng. Hiểu rõ khái niệm tập hợp con và điều kiện để hai tập hợp bằng nhau là bước đệm cần thiết để tiếp cận các khái niệm toán học phức tạp hơn.
Bài viết này trên giaitoan.edu.vn sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu nhất về hai khái niệm này, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức.
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con (tập con) của B. Cho tập hợp A có n phần tử, khi đó số tập hợp con của A là: ({2^n})
1. Lý thuyết
+ Định nghĩa: Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con (tập con) của B.
+ Kí hiệu
\(A \subset B\) (đọc là A chứa trong B) hoặc \(B \supset A\)(đọc là B chứa A).
+ Nhận xét:
· \(A \subset A\) và \(\emptyset \subset A\) với mọi tập A.
· Nếu A không là tập con của B thì ta viết \(A \not\subset B\)
· Nếu \(A \subset B\) hoặc \(A \subset B\) thì ta nói A và B có quan hệ bao hàm.
+ Số tập hợp con:
Cho tập hợp A có n phần tử, khi đó số tập hợp con của A là: \({2^n}\)
+ Biểu đồ Ven:
Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín.
Theo cách này, ta có thể minh họa A là tập con của B như sau:
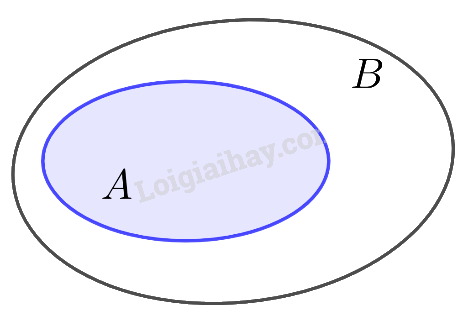
+ Mối quan hệ giữa các tập hợp số
\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
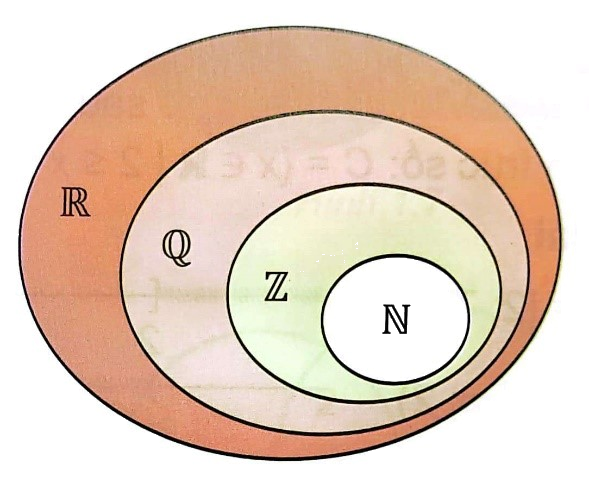
+ Kiểm tra A là tập con của B
\(A \subset B \Leftrightarrow \forall x \in A\) suy ra \(x \in B\)
\(A \not\subset B \Leftrightarrow \exists x \in A:x \notin B\)
+ Định nghĩa: Hai tập hợp bằng nhau
Hai tập hợp A và B gọi là bằng nhau nếu mỗi phần tử của A cũng là phần tử của tập hợp B và ngược lại.
+ Kí hiệu: \(A = B\)
+ Nhận xét: \(A = B \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)
2. Ví dụ minh họa
Ví dụ về tập hợp con
Cho tập hợp \(A = \{ 2;3;7\} \)
Các tập \(B = \{ 2\} ,C = \{ 2;7\} \) là các tập con của A. Kí hiệu: \(B \subset A\), \(C \subset A\)
Các tập \(D = \{ 4;5\} ,E = \{ 0\} \) không là tập con của A. Kí hiệu: \(D \not\subset A\), \(E \not\subset A\)
Ví dụ về hai tập hợp bằng nhau
C là tập hợp các hình thoi có hai đường chéo bằng nhau.
D là tập hợp các hình vuông
Ta có: \(C \subset D\) và \(D \subset C\) nên \(C = D\)
Trong lý thuyết tập hợp, tập hợp A được gọi là tập hợp con của tập hợp B (ký hiệu A ⊆ B) nếu mọi phần tử của A đều là phần tử của B. Nói cách khác, nếu x thuộc A thì x cũng thuộc B.
Ví dụ:
Tập hợp con thực sự: Tập hợp A được gọi là tập hợp con thực sự của tập hợp B (ký hiệu A ⊂ B) nếu A ⊆ B và A ≠ B. Điều này có nghĩa là mọi phần tử của A đều thuộc B, nhưng B có ít nhất một phần tử không thuộc A.
Ví dụ:
Hai tập hợp A và B được gọi là bằng nhau (ký hiệu A = B) nếu chúng có cùng các phần tử. Điều này có nghĩa là mọi phần tử của A đều thuộc B và mọi phần tử của B đều thuộc A.
Ví dụ:
Một số tính chất quan trọng liên quan đến tập hợp con và sự bằng nhau của hai tập hợp:
Các khái niệm về tập hợp con và hai tập hợp bằng nhau có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, bao gồm:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Hiểu rõ về tập hợp con và hai tập hợp bằng nhau là nền tảng quan trọng để học tập và nghiên cứu Toán học. Hy vọng bài viết này trên giaitoan.edu.vn đã cung cấp cho bạn những kiến thức cần thiết và giúp bạn tự tin hơn trong việc giải quyết các bài toán liên quan đến tập hợp.