Bài viết này cung cấp kiến thức cơ bản và nâng cao về hiệu của hai tập hợp và phần bù của một tập hợp trong chương trình toán học. Chúng tôi sẽ trình bày lý thuyết, ví dụ minh họa và bài tập thực hành để giúp bạn hiểu rõ và áp dụng kiến thức một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến những bài giảng toán học online chất lượng, dễ hiểu và phù hợp với mọi trình độ.
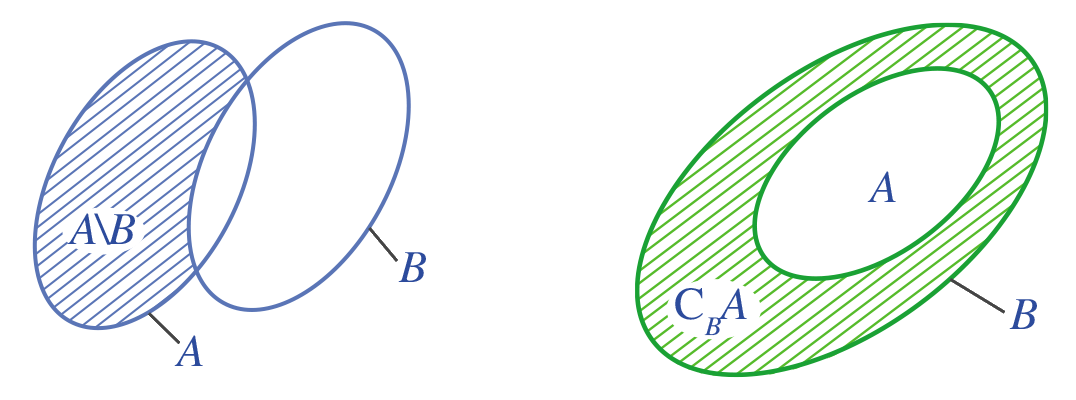
Tập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B. Kí hiệu: (A{rm{backslash }}B)
1. Lý thuyết
+ Định nghĩa: hiệu của A và B
Tập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B.
+ Kí hiệu: \(A{\rm{\backslash }}B\)
Và \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
+ Định nghĩa: Phần bù
Nếu \(A \subset B\) thì hiệu \(A{\rm{\backslash }}B\) gọi là phần bù của A trong B.
+ Kí hiệu: \({C_B}A\)
+ Biểu đồ Ven
+ Xác định hiệu của A và B
Bước 1: Biểu diễn hai tập hợp đó trên trục số.
Bước 2: Gạch bỏ những phần thuộc B trong A. Khi đó phần không bị gạch là hiệu của A và B.
2. Ví dụ minh họa
Ví dụ 1. Cho tập hợp \(C = \{ 2;3;5;7\} \) và \(D = \{ - 1;3;4;5;9\} \)
Tập hợp \(C{\rm{\backslash }}D = \{ 2;7\} \)
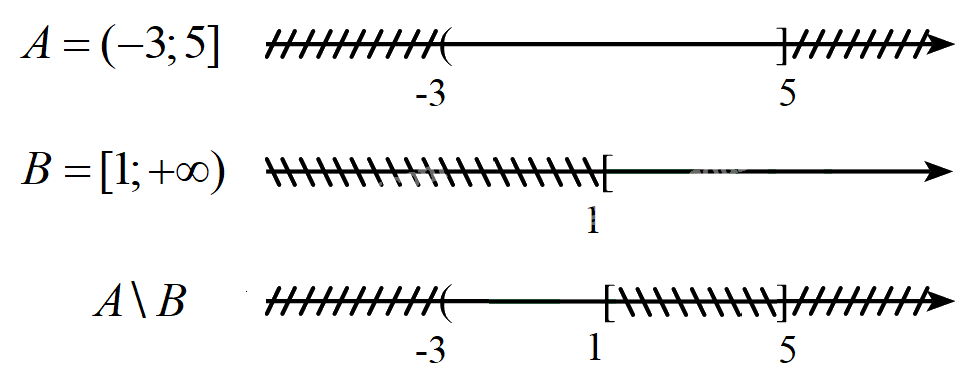
Ví dụ 2. Cho tập hợp \(A = ( - 3;5]\) và \(B = [1; + \infty )\). Xác định \(A{\rm{\backslash }}B\) và \({C_\mathbb{R}}\left( {A \cap B} \right)\).
Vậy \(A{\rm{\backslash }}B = ( - 3;1)\)
Ta có: \(A \cap B = ( - 3;5] \cap [1; + \infty ) = [1;5]\)
Suy ra \({C_\mathbb{R}}\left( {A \cap B} \right) = \mathbb{R}{\rm{\backslash }}[1;5] = ( - \infty ;1) \cup (5; + \infty )\)
Trong lý thuyết tập hợp, hiệu của hai tập hợp A và B, ký hiệu là A \ B (đọc là A trừ B), là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. Nói cách khác, A \ B = {x | x ∈ A và x ∉ B}.
Cho A = {1, 2, 3, 4, 5} và B = {3, 5, 6, 7}. Khi đó:
Phần bù của một tập hợp A, ký hiệu là A', trong một tập hợp vũ trụ U, là tập hợp chứa tất cả các phần tử thuộc U nhưng không thuộc A. Nói cách khác, A' = {x | x ∈ U và x ∉ A}. Tập hợp vũ trụ U phải được xác định rõ ràng trước khi nói về phần bù của một tập hợp.
Cho U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} và A = {2, 4, 6, 8}. Khi đó:
A' = {1, 3, 5, 7, 9, 10}
Sơ đồ Venn là một công cụ trực quan hữu ích để minh họa các phép toán trên tập hợp, bao gồm cả hiệu và phần bù. Trong sơ đồ Venn, tập hợp vũ trụ U được biểu diễn bằng một hình chữ nhật, và các tập hợp con được biểu diễn bằng các hình tròn bên trong hình chữ nhật.
Hiệu A \ B được biểu diễn bằng phần hình tròn của A không giao với hình tròn của B. Phần bù A' được biểu diễn bằng phần hình chữ nhật bên ngoài hình tròn của A.
Bài 1: Cho A = {a, b, c, d} và B = {b, d, e, f}. Tìm A \ B và B \ A.
Bài 2: Cho U = {1, 2, 3, 4, 5, 6, 7} và A = {1, 3, 5}. Tìm A'.
Bài 3: Sử dụng sơ đồ Venn để minh họa hiệu và phần bù của các tập hợp trong Bài 1 và Bài 2.
Hiệu và phần bù của tập hợp có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Để hiểu sâu hơn về lý thuyết tập hợp, bạn có thể tìm hiểu thêm về các khái niệm sau:
Lưu ý: Việc nắm vững các khái niệm cơ bản về tập hợp là nền tảng quan trọng để học tốt các môn toán học khác, đặc biệt là đại số và giải tích.
Hiệu của hai tập hợp và phần bù là những khái niệm quan trọng trong lý thuyết tập hợp. Việc hiểu rõ các khái niệm này sẽ giúp bạn giải quyết các bài toán toán học một cách hiệu quả và áp dụng kiến thức vào thực tế.