Tập Xác Định, Tập Giá Trị Hàm Số | Giải Toán Online

Tập xác định, tập giá trị của hàm số

Tập Xác Định và Tập Giá Trị của Hàm Số - Nền Tảng Toán Học Quan Trọng

Trong chương trình toán học, đặc biệt là ở cấp THPT, việc hiểu rõ về tập xác định và tập giá trị của hàm số là vô cùng quan trọng. Đây là những khái niệm cơ bản giúp chúng ta xác định được những giá trị mà hàm số có thể nhận và những giá trị mà biến độc lập có thể có.

Giaitoan.edu.vn cung cấp tài liệu học tập, bài giảng chi tiết và bài tập thực hành giúp bạn nắm vững kiến thức này một cách dễ dàng và hiệu quả.

Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa. Tập giá trị của hàm số \(y = f(x)\) là tập hợp tất cả các giá trị \(f(x)\) tương ứng với x thuộc tập xác định.

1. Lý thuyết

+ Định nghĩa:

Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa.

Tập giá trị của hàm số \(y = f(x)\) là tập hợp tất cả các giá trị \(f(x)\) tương ứng với x thuộc tập xác định.

+ Kí hiệu:

Tập xác định thường kí hiệu là D. Ta nói: \(x \in D\) là điều kiện xác định của hàm số.

Tập giá trị thường kí hiệu là T.

+ Điều kiện xác định của một số biểu thức

\(\sqrt {f(x)} \) xác định khi \(f(x) \ge 0\)

\(\frac{1}{{f(x)}}\) xác định khi \(f(x) \ne 0\)

\(\frac{1}{{\sqrt {f(x)} }}\) xác định khi \(f(x) > 0\)

2. Ví dụ minh họa

Dạng bảng

Tập xác định là tập hợp các giá trị x có trong bảng.

Tập giá trị là tập hợp các giá trị y có trong bảng.

Ví dụ: Dự báo thời tiết ngày 2/11/2022 tại Hà Nội

Giờ	1	4	7	10	13	16	19	22
Nhiệt độ \({(^o}C)\)	19	17	22	26	29	27	25	23

Tập xác định \(D = \{ 1;4;7;10;13;16;19;22\} \)

Tập giá trị \(T = \{ 19;17;22;26;29;27;25;23\} \).

Dạng biểu đồ

Ví dụ: Dự báo thời tiết ngày 20/11/2021 tại Hà Nội

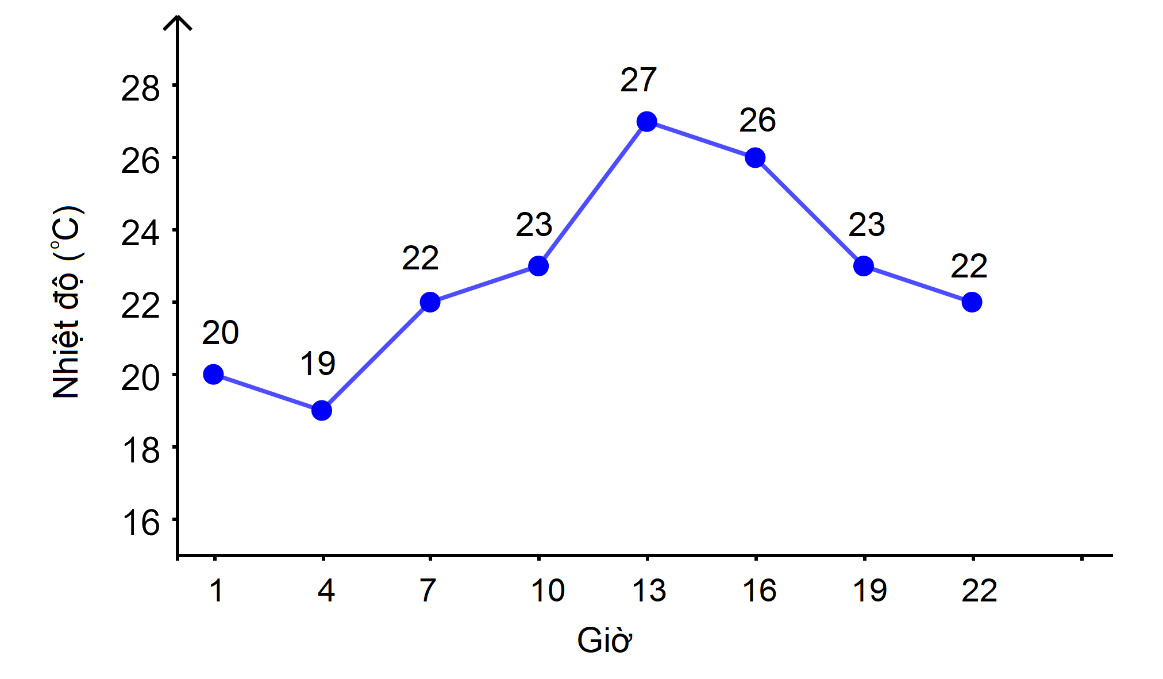
Tập xác định, tập giá trị của hàm số 1

Tập xác định \(D = \{ 1;4;7;10;13;16;19;22\} \)

Tập giá trị \(T = \{ 20;19;22;23;27;26\} \).

Dạng công thức

Ví dụ:

\(y = {x^2} + 3\), biểu thức có nghĩa với mọi \(x \in \mathbb{R}\) nên tập xác định là \(D = \mathbb{R}\)

\(y = \sqrt {x - 1} \), biểu thức có nghĩa nếu \(x - 1 \ge 0\) hay \(x \ge 1\). Vậy tập xác định \(D = [1; + \infty )\)

\(y = \left\{ \begin{array}{l} - 3x + 5\quad \quad x \le 1\\2{x^2}\quad \quad \quad \;\;x > 2\end{array} \right.\), ta xác đinh được y với \(x \le 1\) hoặc \(x > 2\), do đó tập xác định là \(D = ( - \infty ;1] \cup (2; + \infty )\)

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Tập xác định, tập giá trị của hàm số đặc sắc thuộc chuyên mục sgk toán 10 trên nền tảng toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Tập Xác Định và Tập Giá Trị của Hàm Số: Tổng Quan

Hàm số là một công cụ toán học quan trọng, mô tả mối quan hệ giữa một biến độc lập (thường là x) và một biến phụ thuộc (thường là y). Tuy nhiên, không phải giá trị nào của biến độc lập cũng có thể được sử dụng để tính giá trị của hàm số. Tập xác định chính là tập hợp tất cả các giá trị mà biến độc lập có thể nhận.

1. Tập Xác Định của Hàm Số

Tập xác định (ký hiệu là D) của hàm số f(x) là tập hợp tất cả các giá trị x sao cho f(x) có nghĩa. Để tìm tập xác định, chúng ta cần xem xét các điều kiện sau:

Mẫu số khác 0: Nếu hàm số có dạng phân thức, mẫu số phải khác 0.
Căn bậc chẵn: Biểu thức dưới dấu căn bậc chẵn phải lớn hơn hoặc bằng 0.
Logarit: Cơ số của logarit phải dương và khác 1, và biểu thức bên trong logarit phải dương.
Hàm số lượng giác: Một số hàm lượng giác có tập xác định bị giới hạn (ví dụ: tan(x) xác định khi x ≠ π/2 + kπ, k ∈ Z).

Ví dụ 1: Tìm tập xác định của hàm số f(x) = √(x - 2)

Điều kiện xác định: x - 2 ≥ 0 ⇔ x ≥ 2. Vậy tập xác định của hàm số là D = [2, +∞).

2. Tập Giá Trị của Hàm Số

Tập giá trị (ký hiệu là V) của hàm số f(x) là tập hợp tất cả các giá trị y mà hàm số có thể nhận được khi x thuộc tập xác định. Việc tìm tập giá trị thường khó khăn hơn so với tìm tập xác định và đòi hỏi sự hiểu biết sâu sắc về tính chất của hàm số.

Các phương pháp tìm tập giá trị:

Sử dụng tính chất của hàm số: Ví dụ, hàm số y = x² luôn có giá trị không âm, do đó tập giá trị là [0, +∞).
Sử dụng đạo hàm: Tìm cực trị của hàm số để xác định giá trị lớn nhất và nhỏ nhất.
Biến đổi hàm số: Đặt t = f(x) và tìm tập xác định của t.

Ví dụ 2: Tìm tập giá trị của hàm số f(x) = x² - 4x + 3

Ta có f(x) = (x - 2)² - 1. Vì (x - 2)² ≥ 0 với mọi x, nên f(x) ≥ -1. Vậy tập giá trị của hàm số là V = [-1, +∞).

3. Mối Quan Hệ Giữa Tập Xác Định và Tập Giá Trị

Tập xác định và tập giá trị là hai khái niệm quan trọng và có mối liên hệ mật thiết với nhau. Việc hiểu rõ cả hai khái niệm này giúp chúng ta phân tích và giải quyết các bài toán liên quan đến hàm số một cách hiệu quả.

4. Ứng Dụng của Tập Xác Định và Tập Giá Trị

Kiến thức về tập xác định và tập giá trị được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học, như:

Giải phương trình và bất phương trình: Xác định miền nghiệm của phương trình và bất phương trình.
Vẽ đồ thị hàm số: Xác định các điểm không xác định và các điểm giới hạn của đồ thị.
Tính giới hạn và đạo hàm: Đảm bảo rằng các phép tính này được thực hiện trên tập xác định của hàm số.

5. Bài Tập Vận Dụng

Hãy thử giải các bài tập sau để củng cố kiến thức về tập xác định và tập giá trị:

Tìm tập xác định của hàm số f(x) = 1/(x² - 1).
Tìm tập giá trị của hàm số f(x) = sin(x).
Tìm tập xác định và tập giá trị của hàm số f(x) = log₂(x + 3).

Kết Luận

Tập xác định và tập giá trị là những khái niệm cơ bản nhưng vô cùng quan trọng trong toán học. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán liên quan đến hàm số một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.