Sự biến thiên của hàm số là một trong những chủ đề quan trọng trong chương trình Toán học, đặc biệt là ở cấp THPT.
Hiểu rõ về sự biến thiên của hàm số giúp học sinh phân tích được tính chất của hàm số, dự đoán được xu hướng thay đổi của hàm số và giải quyết các bài toán liên quan một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập sự biến thiên hàm số một cách dễ hiểu nhất.
Hàm số \(y = f(x)\) đồng biến (tăng) trên khoảng (a;b) nếu \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\) Hàm số \(y = f(x)\) nghịch biến (giảm) trên khoảng (a;b) nếu \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
1. Lý thuyết
Cho hàm số \(y = f(x)\) xác định trên khoảng (a;b).
+ Định nghĩa:
Hàm số \(y = f(x)\) đồng biến (tăng) trên khoảng (a;b) nếu
\(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
Hàm số \(y = f(x)\) nghịch biến (giảm) trên khoảng (a;b) nếu
\(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
Xét sự biến thiên của hàm số là tìm các khoảng hàm số đồng biến và các khoảng hàm số nghịch biến.
+ Mô tả sự biến thiên bằng bảng biến thiên
Kết quả xét sự biến thiên được tổng kết trong mộtbảng biến thiên. Trong đó:
Dấu mũi tên đi lên diễn tả hàm số đồng biến trên khoảng tương ứng.
Dấu mũi tên đi xuống diễn tả hàm số nghịch biến trên khoảng tương ứng.
+ Mô tả sự biến thiên bằng đồ thị
Hàm số đồng biến trên khoảng (a;b) khi và chỉ khi đồ thị hàm số có dạng “đi lên” (từ trái sang phải) trên khoảng đó.
Hàm số nghịch biến trên khoảng (a;b) khi và chỉ khi đồ thị hàm số có dạng “đi xuống” (từ trái sang phải) trên khoảng đó.
+ Hàm số bậc nhất \(y = ax + b\) đồng biến trên \(\mathbb{R}\) nếu \(a > 0\), nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).
2. Ví dụ minh họa
Ví dụ 1.Chứng minh hàm số \(y = 2{x^2}\)đồng biến trên khoảng\((0; + \infty )\)
Xét hai số bất kì \({x_1},{x_2} \in (0; + \infty )\) sao cho \({x_1} < {x_2}\).
Ta có: \(0 < {x_1} < {x_2}\) nên \(2{x_1}^2 < 2{x_2}^2\) hay \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến trên khoảng \((0; + \infty )\)
Ví dụ 2.Cho bảng biến thiên của hàm số \(y = 2{x^2} + 1\)
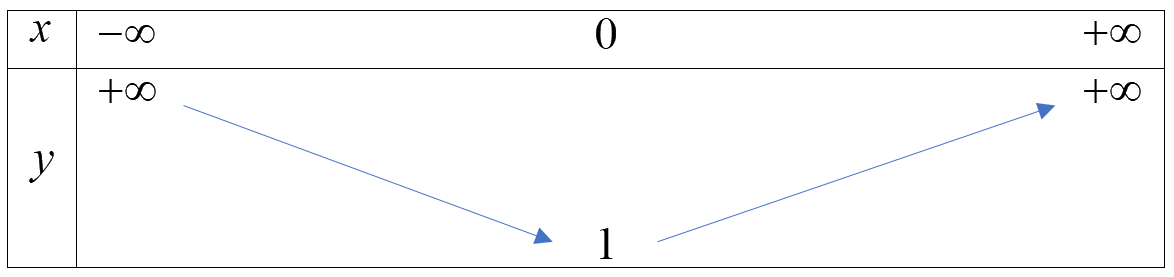
Ví dụ 3.Cho đồ thị của hàm số \(y = f(x)\)
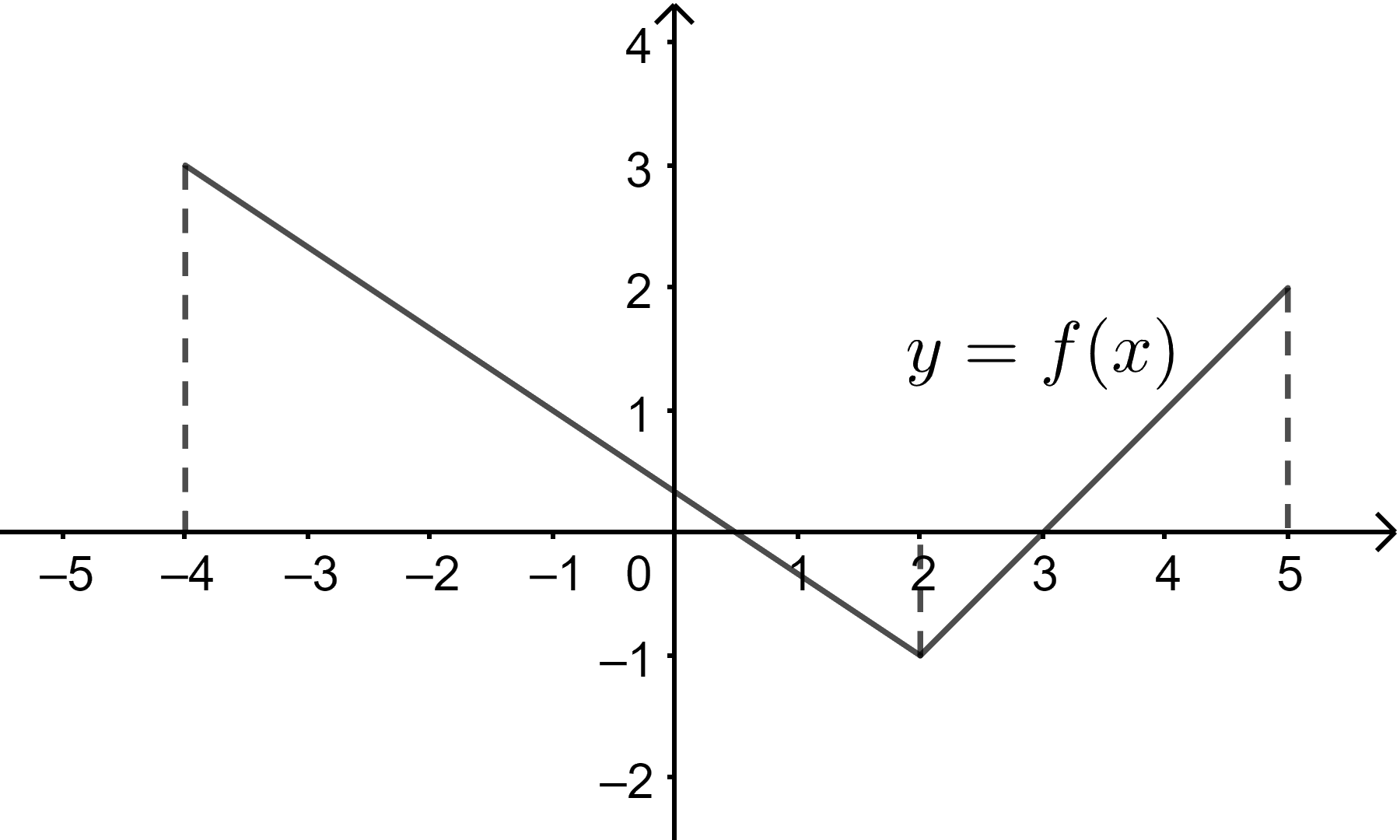
Hàm số \(y = f(x)\) đồng biến trên khoảng (2;5)
Hàm số \(y = f(x)\) nghịch biến trên khoảng (-4;2)
Sự biến thiên của hàm số là một khái niệm quan trọng trong giải tích, giúp ta hiểu rõ hơn về hành vi của hàm số trên một khoảng xác định. Việc nghiên cứu sự biến thiên của hàm số bao gồm việc xác định khoảng đồng biến, khoảng nghịch biến, cực trị, giới hạn và các tính chất khác của hàm số.
Một hàm số f(x) được gọi là đồng biến trên một khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≤ f(x2). Hàm số được gọi là nghịch biến trên một khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≥ f(x2).
Để xác định khoảng đồng biến, nghịch biến của hàm số, ta thường sử dụng đạo hàm của hàm số:
Cực đại của hàm số f(x) là giá trị lớn nhất của hàm số trong một lân cận nào đó. Cực tiểu của hàm số f(x) là giá trị nhỏ nhất của hàm số trong một lân cận nào đó.
Để tìm cực trị của hàm số, ta thực hiện các bước sau:
Bảng biến thiên là một công cụ hữu ích để tóm tắt các thông tin về sự biến thiên của hàm số, bao gồm khoảng đồng biến, khoảng nghịch biến, cực trị, giới hạn và các điểm đặc biệt khác.
Xét hàm số f(x) = x3 - 3x2 + 2. Ta có f'(x) = 3x2 - 6x = 3x(x - 2). Giải phương trình f'(x) = 0, ta được x = 0 và x = 2.
Khảo sát dấu của f'(x):
| Khoảng | f'(x) | f(x) |
|---|---|---|
| (-∞, 0) | + | Đồng biến |
| (0, 2) | - | Nghịch biến |
| (2, +∞) | + | Đồng biến |
Vậy hàm số đồng biến trên (-∞, 0) và (2, +∞), nghịch biến trên (0, 2). Hàm số đạt cực đại tại x = 0 với giá trị f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị f(2) = -2.
Nghiên cứu sự biến thiên của hàm số có nhiều ứng dụng trong thực tế, như:
Để nắm vững kiến thức về sự biến thiên của hàm số, bạn nên luyện tập thường xuyên các bài tập khác nhau. Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Hy vọng với những kiến thức và phương pháp được trình bày trên, bạn sẽ hiểu rõ hơn về sự biến thiên của hàm số và có thể áp dụng chúng vào việc giải quyết các bài toán thực tế.