Bài viết này cung cấp kiến thức đầy đủ và dễ hiểu về các tập hợp con của tập số thực R trong chương trình toán học. Chúng ta sẽ cùng nhau khám phá định nghĩa, các loại tập hợp con phổ biến và cách ứng dụng chúng trong giải toán.
Nội dung được trình bày một cách logic, kèm theo nhiều ví dụ minh họa và bài tập thực hành để bạn có thể tự kiểm tra và củng cố kiến thức.
Kí hiệu ( - infty ) đọc là âm vô cực (hoặc âm vô cùng) Kí hiệu ( + infty ) đọc là dương vô cực (hoặc dương vô cùng)
1. Lý thuyết
Cho \(a\) và \(b\) là hai số thực với \(a < b\)
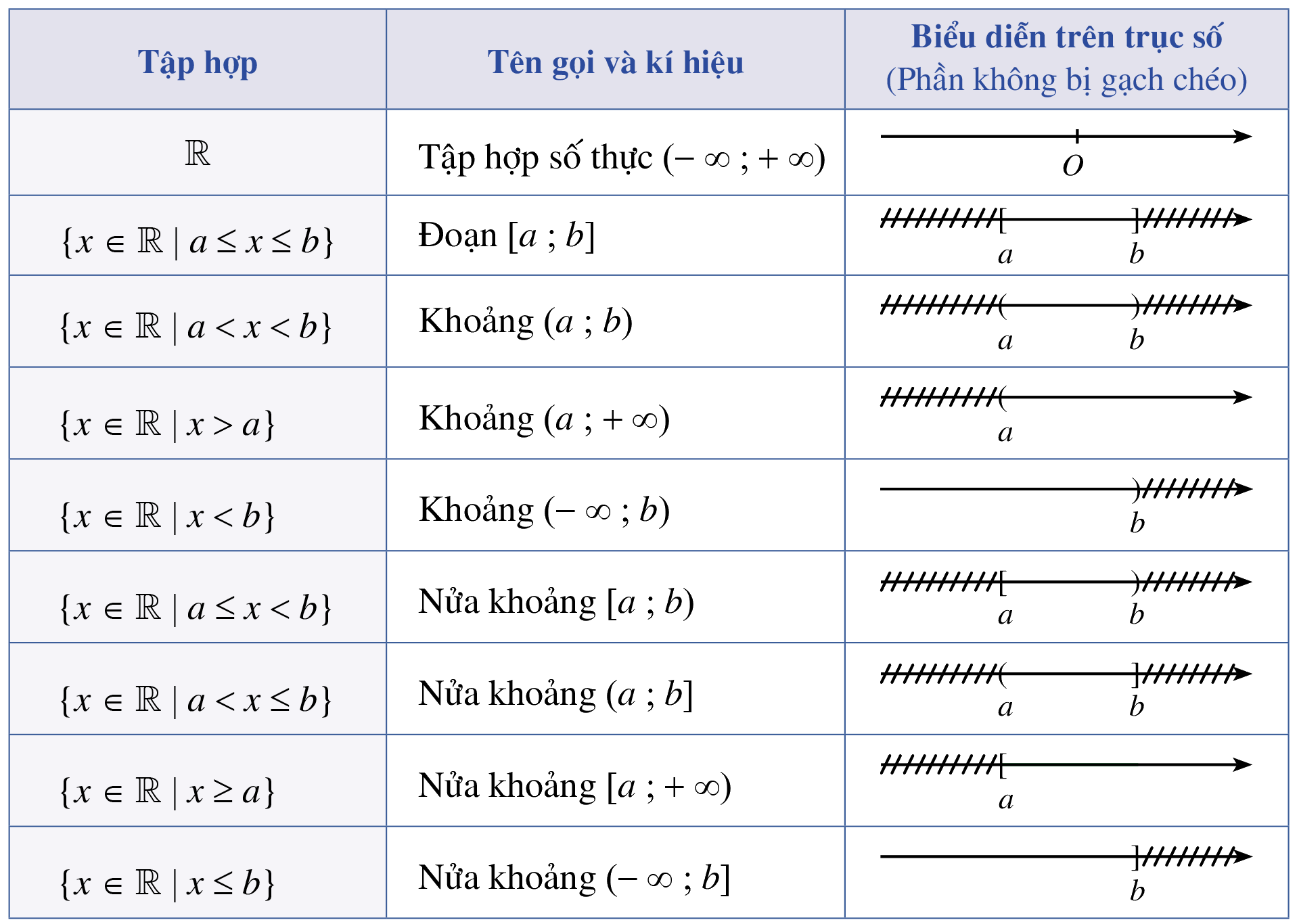
Kí hiệu \( - \infty \) đọc là âm vô cực (hoặc âm vô cùng)
Kí hiệu \( + \infty \) đọc là dương vô cực (hoặc dương vô cùng)
\(a\) và \(b\) được gọi là các đầu mút của các đoạn, khoảng, nửa khoảng
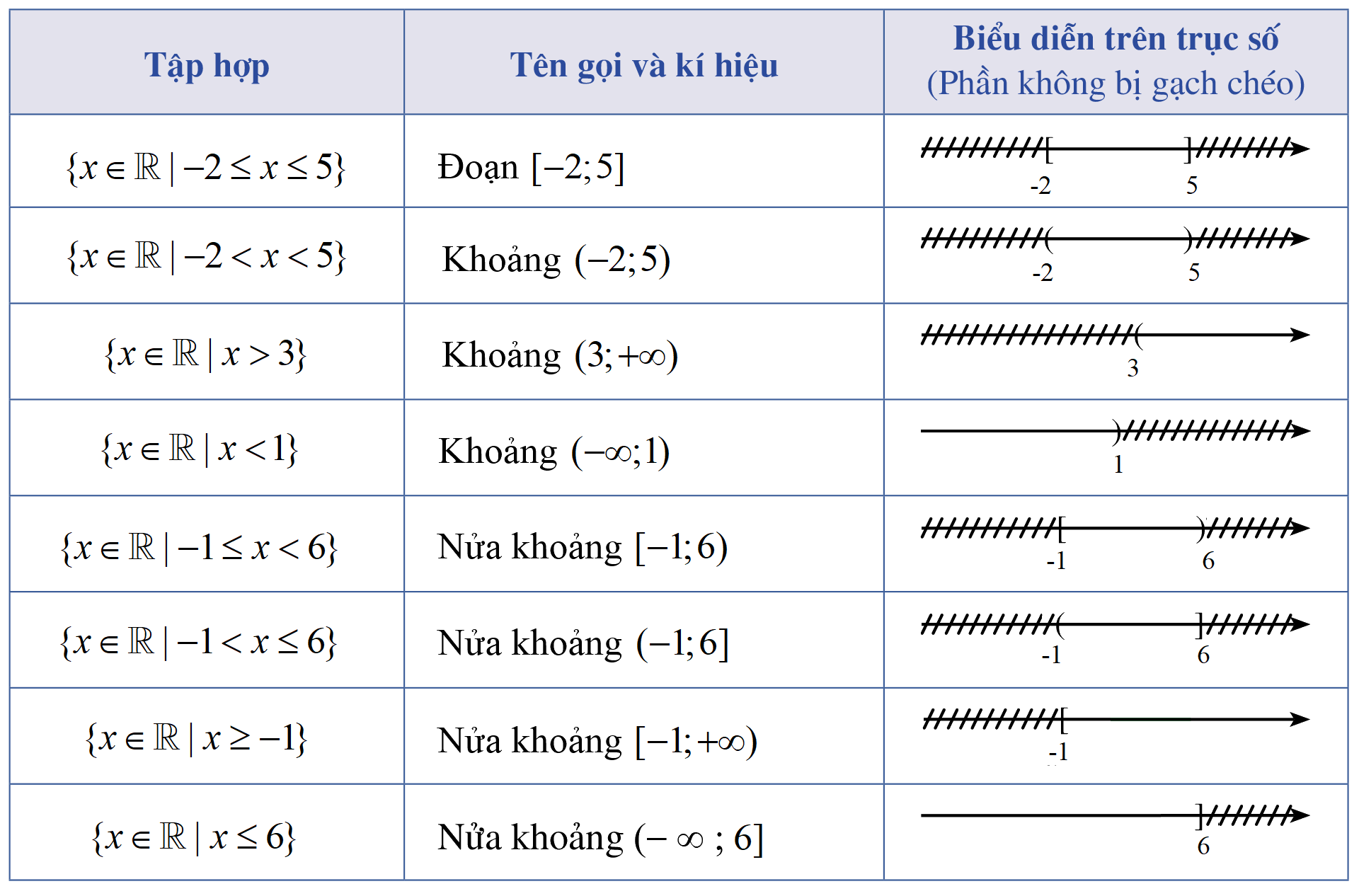
2. Ví dụ minh họa
Tập số thực (ký hiệu là R) bao gồm tất cả các số có thể biểu diễn trên trục số, bao gồm các số hữu tỉ (Q) và các số vô tỉ (I). Nói cách khác, R = Q ∪ I. Hiểu rõ về tập số thực là nền tảng để nắm vững các khái niệm về tập hợp con của R.
Một tập hợp A được gọi là tập hợp con của tập hợp B (ký hiệu là A ⊆ B) nếu mọi phần tử thuộc A đều thuộc B. Tức là, nếu x ∈ A thì x ∈ B.
Ví dụ: Nếu A = {1, 2} và B = {1, 2, 3}, thì A ⊆ B.
Cho A = [1, 3] và B = (2, 5). Hãy tìm:
Các khái niệm về tập hợp con của R được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học, bao gồm:
1. Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B, A ∩ B, A \ B.
2. Biểu diễn khoảng (-2, 4] trên trục số và xác định các phần tử thuộc khoảng này.
3. Cho A = Q và B = I. A ∪ B bằng tập hợp nào?
Việc nắm vững kiến thức về các tập hợp con của R là vô cùng quan trọng để học tốt toán học. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.