Trong toán học, đặc biệt là trong lý thuyết tập hợp, Hợp của hai tập hợp là một khái niệm cơ bản và quan trọng. Bài viết này tại giaitoan.edu.vn sẽ cung cấp cho bạn định nghĩa, tính chất, các ví dụ minh họa và bài tập thực hành để hiểu rõ hơn về khái niệm này.
Chúng ta sẽ cùng nhau khám phá cách xác định hợp của hai tập hợp, các quy tắc liên quan và ứng dụng của nó trong việc giải quyết các bài toán toán học.
Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B gọi là hợp của hai tập hợp A và B. Kí hiệu: (A cup B)
1. Lý thuyết
+ Định nghĩa:
Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B gọi là hợp của hai tập hợp A và B.
+ Kí hiệu: \(A \cup B\)
+ Nhận xét
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
\(A \cup B = B \Leftrightarrow A \subset B\)
+ Biểu đồ Ven
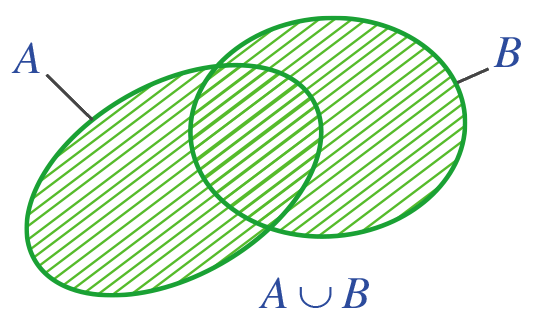
+ Xác định hợp của hai tập con của \(\mathbb{R}\)
Bước 1: Biểu diễn hai tập hợp đó trên trục số.
Bước 2: Hợp hai tập hợp là phần không bị gạch ở cả hai tập hợp.
2. Ví dụ minh họa
Ví dụ 1. Cho tập hợp \(C = \{ 2;3;5;7\} \) và \(D = \{ - 1;2;4;5;9\} \)
Tập hợp \(C \cup D = \{ 2;3;5;7; - 1;4;9\} \)
Ví dụ 2. Cho tập hợp \(A = ( - 3;5]\) và \(B = [1; + \infty )\). Xác định \(A \cup B\) và biểu diễn trên trục số.
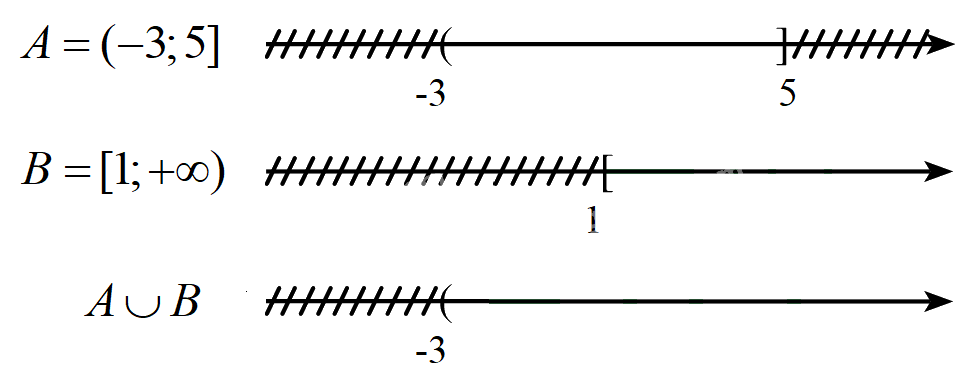
Vậy \(A \cup B = ( - 3; + \infty )\)
Trong lý thuyết tập hợp, tập hợp là một khái niệm nền tảng. Một tập hợp là một bộ sưu tập các đối tượng riêng biệt, được gọi là các phần tử. Hợp của hai tập hợp, ký hiệu là A ∪ B, là một tập hợp chứa tất cả các phần tử thuộc A, thuộc B, hoặc thuộc cả A và B. Nói cách khác, nó bao gồm tất cả các phần tử của cả hai tập hợp, loại bỏ các phần tử trùng lặp.
Công thức toán học để biểu diễn hợp của hai tập hợp A và B là:
A ∪ B = {x | x ∈ A hoặc x ∈ B}
Trong đó:
Xét hai tập hợp sau:
A = {1, 2, 3}
B = {3, 4, 5}
Hợp của hai tập hợp A và B là:
A ∪ B = {1, 2, 3, 4, 5}
Điều quan trọng là phải phân biệt phép hợp (∪) với phép giao (∩) của hai tập hợp. Trong khi hợp của hai tập hợp chứa tất cả các phần tử thuộc ít nhất một trong hai tập hợp, giao của hai tập hợp chỉ chứa các phần tử thuộc cả hai tập hợp.
Ví dụ, với A = {1, 2, 3} và B = {3, 4, 5}, giao của A và B là:
A ∩ B = {3}
Hợp của hai tập hợp có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Dưới đây là một số bài tập để bạn luyện tập về hợp của hai tập hợp:
Khái niệm hợp có thể được mở rộng cho nhiều hơn hai tập hợp. Hợp của n tập hợp A1, A2, ..., An là tập hợp chứa tất cả các phần tử thuộc ít nhất một trong các tập hợp đó.
A1 ∪ A2 ∪ ... ∪ An = {x | x ∈ Ai với ít nhất một i từ 1 đến n}
Hợp của hai tập hợp là một khái niệm quan trọng trong lý thuyết tập hợp và có nhiều ứng dụng trong toán học và các lĩnh vực khác. Hiểu rõ định nghĩa, tính chất và cách sử dụng phép hợp sẽ giúp bạn giải quyết các bài toán toán học một cách hiệu quả hơn. Hãy luyện tập thường xuyên để nắm vững kiến thức này!