Nghiệm của hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm

Nghiệm của Hệ Bất Phương Trình Bậc Nhất Hai Ẩn: Hướng Dẫn Chi Tiết

Bài viết này sẽ cung cấp cho bạn kiến thức nền tảng và phương pháp giải quyết các bài toán liên quan đến nghiệm của hệ bất phương trình bậc nhất hai ẩn. Chúng ta sẽ cùng nhau tìm hiểu cách xác định nghiệm, biểu diễn miền nghiệm và ứng dụng của kiến thức này trong thực tế.

Giaitoan.edu.vn tự hào mang đến những bài giảng chất lượng, dễ hiểu, giúp bạn nắm vững kiến thức toán học một cách nhanh chóng và hiệu quả.

Cặp số \(({x_0};{y_0})\) được gọi là một nghiệm của hệ bất phương trình bậc nhất hai ẩn nếu nó là nghiệm chung của tất cả các bất phương trình trong hệ. Trong mặt phẳng tọa độ \(Oxy\), miền nghiệm của hệ bất phương trình bậc nhất hai ẩn là tập hợp các điểm \(({x_0};{y_0})\) là nghiệm của hệ bất phương trình đó.

1. Lý thuyết

+ Định nghĩa:

Cặp số \(({x_0};{y_0})\) được gọi là một nghiệm của hệ bất phương trình bậc nhất hai ẩn nếu nó là nghiệm chung của tất cả các bất phương trình trong hệ.

Trong mặt phẳng tọa độ \(Oxy\), miền nghiệm của hệ bất phương trình bậc nhất hai ẩn là tập hợp các điểm \(({x_0};{y_0})\) là nghiệm của hệ bất phương trình đó.

+ Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn

Bước 1: Biểu diễn miền nghiệm của mỗi bất phương trình trong hệ trên cùng mặt phẳng tọa độ. Gạch bỏ miền không là nghiệm.

Bước 2: Phần không bị gạch là miền nghiệm của hệ.

+ Biểu diễn miền nghiệm của bất phương trình \(ax + by \le c\)

Bước 1: Vẽ đường thẳng \(\Delta :ax + by = c\)

Bước 2: Lấy điểm \(A({x_0};{y_0})\) không thuộc \(\Delta \). Tính \(a{x_0} + b{y_0}\) rồi so sánh với c.

Bước 3: Kết luận

Nếu \(a{x_0} + b{y_0} < c\) thì miền nghiệm là nửa mặt phẳng (kể cả bờ \(\Delta \)) chứa điểm \(A({x_0};{y_0})\).

Nếu \(a{x_0} + b{y_0} > c\) thì miền nghiệm là nửa mặt phẳng (kể cả bờ \(\Delta \)) không chứa điểm \(A({x_0};{y_0})\).

2. Ví dụ minh họa

+ Nghiệm của hệ bất phương trình bậc nhất hai ẩn:

Cặp số \((7;0)\) là một nghiệm của hệ BPT \(\left\{ {\begin{array}{*{20}{l}}{2x + 3y > 10}\\{x - y \le 7}\end{array}} \right.\)

Cặp số \((0;0)\) không là nghiệm của hệ BPT \(\left\{ {\begin{array}{*{20}{l}}{2x + 3y > 10}\\{x - y \le 7}\end{array}} \right.\)

Điểm \((2;1)\) thuộc miền nghiệm của hệ BPT \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge 0\\2x - 3y < 10\end{array}\\{x + 2y \le 7}\end{array}} \right.\)

Điểm \(( - 1;0)\) không thuộc miền nghiệm của hệ BPT \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge 0\\2x - 3y < 10\end{array}\\{x + 2y \le 7}\end{array}} \right.\)

+ Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - y > 2\\3x + y \le 6\end{array} \right.\)

Bước 1:

Xác định miền nghiệm của BPT \(2x - y > 2\)

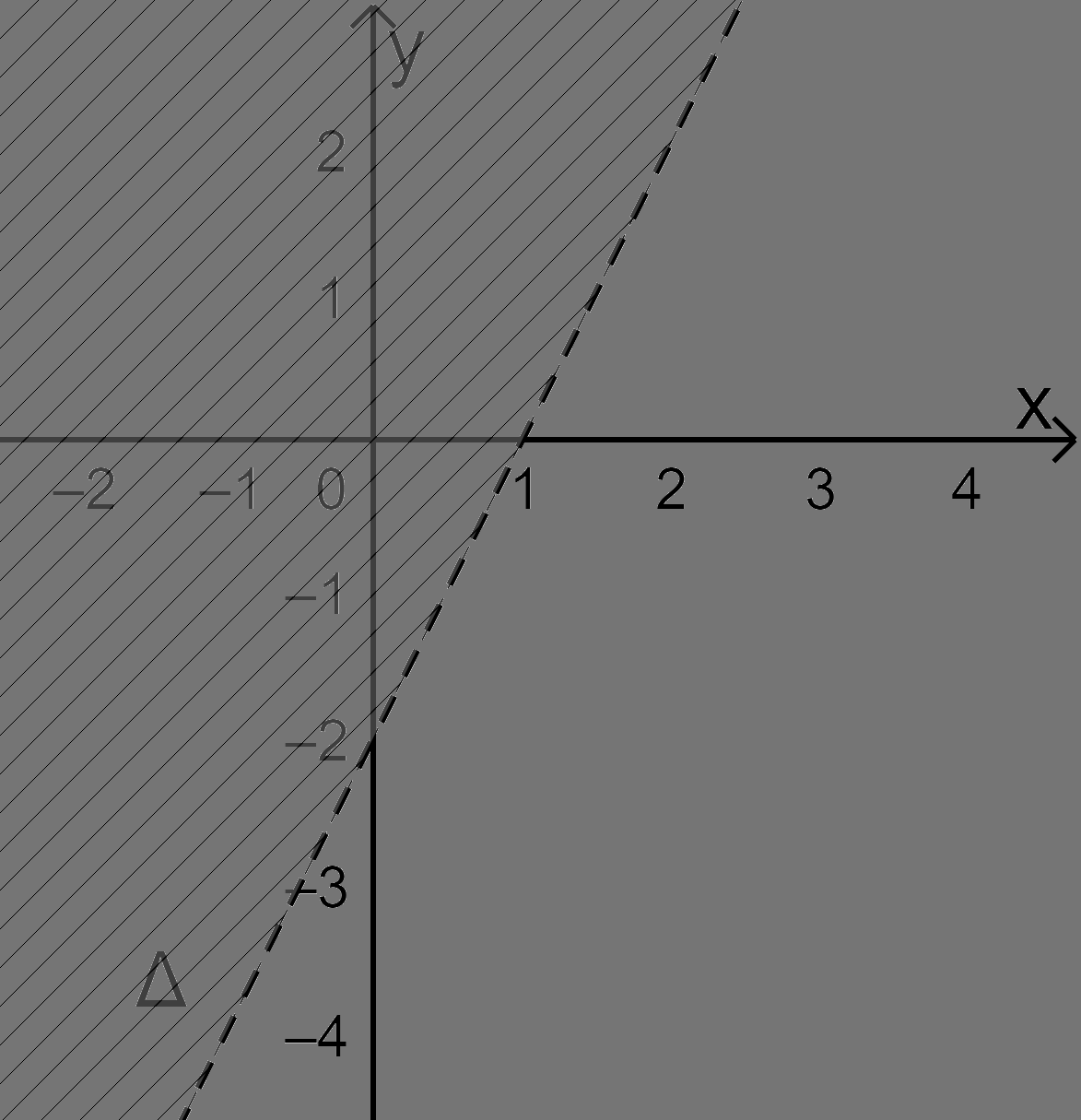
Vẽ đường thẳng \(\Delta :2x - y = 2\) (nét đứt) đi qua (1;0) và (0; -2).

Lấy điểm \(O(0;0)\) không thuộc \(\Delta \). Ta có \(2.0 - 0 = 0\) và \(c = 2\).

Vì \(2.0 - 0 = 0 < 2\) nên điểm \(O(0;0)\) không thuộc miền nghiệm.

Vậy miền nghiệm của BPT \(2x - y > 2\) là nửa mặt phẳng (không kể bờ \(\Delta \)) không chứa điểm \(O(0;0)\) (miền không gạch chéo).

Nghiệm của hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm 1

Xác định miền nghiệm của BPT \(3x + y \le 6\)

Vẽ đường thẳng \(d:3x + y = 6\) (nét liền) đi qua (2;0) và (0; 6).

Lấy điểm \(O(0;0)\) không thuộc \(d\). Ta có \(3.0 + 0 = 0\) và \(c = 6\).

Vì \(3.0 + 0 = 0 \le 6\) nên điểm \(O(0;0)\) thuộc miền nghiệm.

Vậy miền nghiệm của BPT \(3x + y \le 6\) là nửa mặt phẳng (kể cả bờ \(d\)) chứa điểm \(O(0;0)\) (miền không gạch chéo).

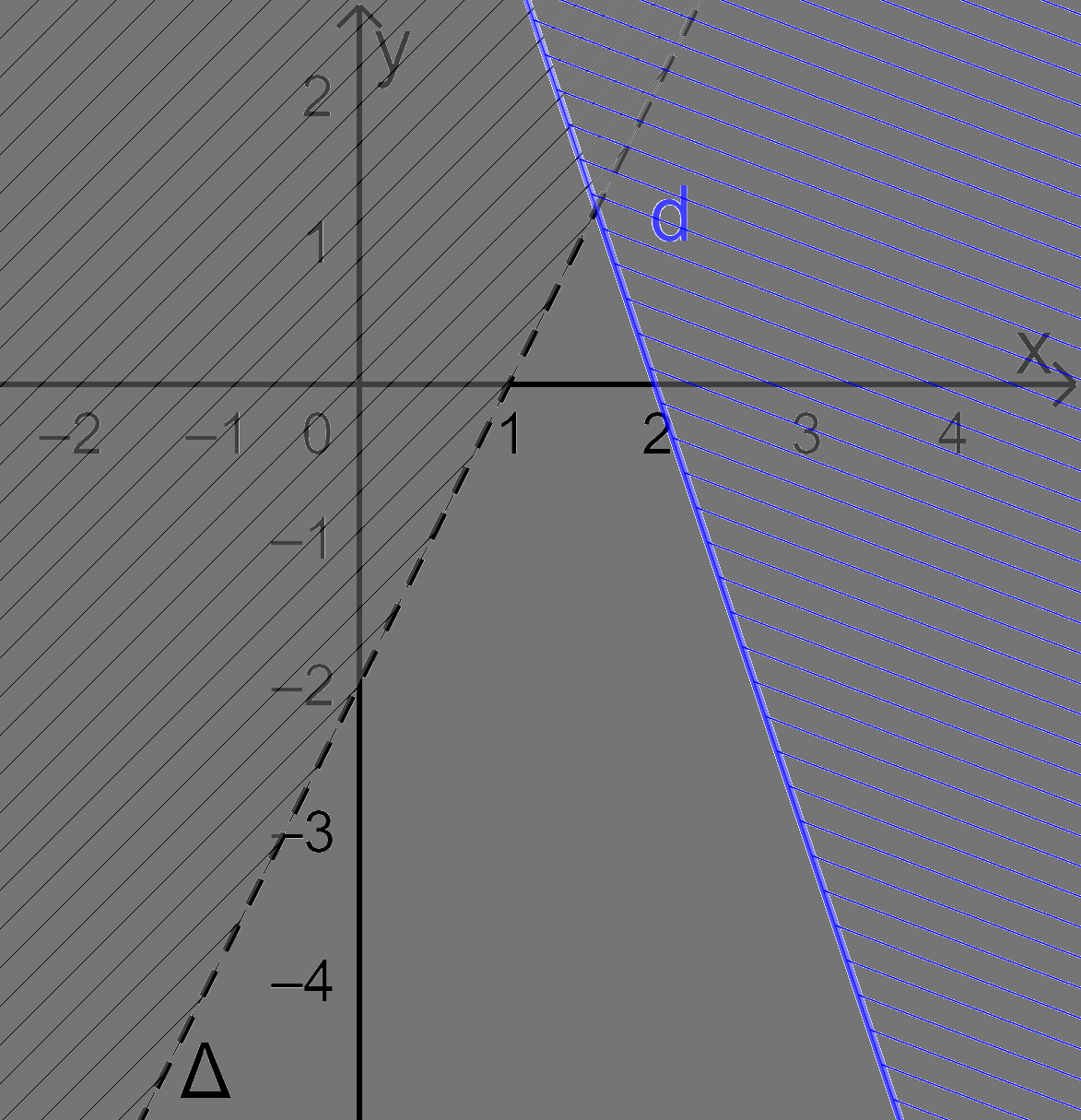
Nghiệm của hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm 2

Bước 2: Kết luận

Miền không bị gạch (kể cả d, không kể \(\Delta \)) là miền nghiệm của hệ bất phương trình đã cho.

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Nghiệm của hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm đặc sắc thuộc chuyên mục giải bài tập toán 10 trên nền tảng soạn toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Nghiệm của Hệ Bất Phương Trình Bậc Nhất Hai Ẩn: Tổng Quan

Hệ bất phương trình bậc nhất hai ẩn là một tập hợp các bất phương trình, mỗi bất phương trình chứa hai biến bậc nhất. Việc tìm nghiệm của hệ bất phương trình này là xác định tất cả các cặp giá trị (x, y) thỏa mãn đồng thời tất cả các bất phương trình trong hệ. Miền nghiệm của hệ là tập hợp tất cả các điểm (x, y) trên mặt phẳng tọa độ thỏa mãn tất cả các bất phương trình trong hệ.

Định Nghĩa và Khái Niệm Cơ Bản

Một hệ bất phương trình bậc nhất hai ẩn có dạng:

a₁x + b₁y ≤ c₁
a₂x + b₂y ≤ c₂
...
a_nx + b_ny ≤ c_n

Trong đó, a_i, b_i, c_i là các số thực với i = 1, 2, ..., n.

Phương Pháp Giải Hệ Bất Phương Trình Bậc Nhất Hai Ẩn

Biểu diễn các bất phương trình trên mặt phẳng tọa độ: Mỗi bất phương trình bậc nhất hai ẩn tương ứng với một nửa mặt phẳng. Vùng nửa mặt phẳng thỏa mãn bất phương trình là miền nghiệm của bất phương trình đó.
Xác định miền nghiệm của hệ: Miền nghiệm của hệ là giao của các miền nghiệm của từng bất phương trình.
Kiểm tra các điểm thuộc miền nghiệm: Chọn một điểm bất kỳ thuộc miền nghiệm để kiểm tra xem nó có thỏa mãn tất cả các bất phương trình trong hệ hay không.

Biểu Diễn Miền Nghiệm

Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn có thể là một đa giác lồi vô hạn, một đa giác lồi hữu hạn hoặc một tập hợp các điểm rời rạc. Để biểu diễn miền nghiệm, ta thường vẽ các đường thẳng tương ứng với các bất phương trình và tô đậm vùng thỏa mãn.

Ví Dụ Minh Họa

Xét hệ bất phương trình sau:

x + y ≤ 2
x - y ≤ 1
x ≥ 0
y ≥ 0

Để giải hệ này, ta thực hiện các bước sau:

Vẽ các đường thẳng x + y = 2, x - y = 1, x = 0, y = 0.
Xác định miền nghiệm của từng bất phương trình.
Tìm giao của các miền nghiệm. Miền nghiệm của hệ là tứ giác có các đỉnh (0, 0), (1, 0), (2, 0), (1, 1).

Ứng Dụng của Nghiệm Hệ Bất Phương Trình Bậc Nhất Hai Ẩn

Nghiệm của hệ bất phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, chẳng hạn như:

Bài toán quy hoạch tuyến tính: Tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm mục tiêu trên một miền nghiệm.
Bài toán tối ưu hóa: Tìm các giải pháp tối ưu cho một bài toán có nhiều ràng buộc.
Bài toán kinh tế: Phân tích các mối quan hệ giữa các biến số kinh tế.

Lưu Ý Quan Trọng

Khi vẽ các đường thẳng, cần chú ý đến dấu của bất phương trình. Nếu bất phương trình là ≤ hoặc ≥, đường thẳng được vẽ là đường liền nét. Nếu bất phương trình là < hoặc >, đường thẳng được vẽ là đường đứt nét.
Khi xác định miền nghiệm, cần kiểm tra xem các điểm thuộc miền nghiệm có thỏa mãn tất cả các bất phương trình trong hệ hay không.

Bài Tập Thực Hành

Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:

Giải hệ bất phương trình: x + 2y ≤ 4, x - y ≥ 1, x ≥ 0, y ≥ 0.
Tìm miền nghiệm của hệ bất phương trình: 2x + y ≤ 6, x + y ≤ 4, x ≥ 0, y ≥ 0.

Kết Luận

Việc nắm vững kiến thức về nghiệm của hệ bất phương trình bậc nhất hai ẩn và biểu diễn miền nghiệm là rất quan trọng trong quá trình học toán. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin giải quyết các bài toán liên quan.