Bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F=ax+by trên một miền đa giác là một chủ đề quan trọng trong chương trình Toán học, đặc biệt là trong các lớp 10, 11, 12. Đây là một ứng dụng thực tế của phương pháp tọa độ và các kiến thức về bất đẳng thức.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập đa dạng để giúp bạn nắm vững phương pháp giải quyết bài toán này một cách hiệu quả nhất.
Bước 1: Đặt ẩn (hai ẩn x, y), từ giả thiết lập hệ bất phương trình bậc nhất hai ẩn. Bước 2: Xác định miền đa giác nghiệm và tọa độ đỉnh của đa giác đó. Bước 3: Tính gía trị cuả F tại các đỉnh của đa giác. So sánh các giá trị thu được. Bước 4: Kết luận.
1. Lý thuyết
Nhiều bài toán thực tế được đưa về bài toán tìm giá trị lớn nhất (nhỏ nhất) của biểu thức \(F = ax + by\) trên một miền đa giác – miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn.
Người ta chứng minh được F đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của đa giác.
+ Các bước giải
Bước 1: Đặt ẩn (hai ẩn x, y), từ giả thiết lập hệ bất phương trình bậc nhất hai ẩn.
Bước 2: Xác định miền đa giác nghiệm và tọa độ đỉnh của đa giác đó.
Bước 3: Tính gía trị cuả F tại các đỉnh của đa giác. So sánh các giá trị thu được.
Bước 4: Kết luận.
2. Ví dụ minh họa
Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?
Lời giải chi tiết
Gọi diện tích trồng cà chua và cải bắp lần lượt là x, y (đơn vị: \({m^2}\)). \((x,y \ge 0)\)
Mảnh vườn rộng \(8{m^2}\) nên ta có: \(x + y \le 8\)
Khi trồng x \({m^2}\) cà chua thì cần \(20x\) công và thu được \(300x\) nghìn đồng
Khi trồng y \({m^2}\) cải bắp thì cần \(30x\) công và thu được \(400x\) nghìn đồng
Tổng số công không quá 180 nên ta có: \(20x + 30y \le 180\) hay \(2x + 3y \le 18\)
Tổng số tiền thu được là: \(F(x;y) = 300x + 400y\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 8\\0 \le y \le 8\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
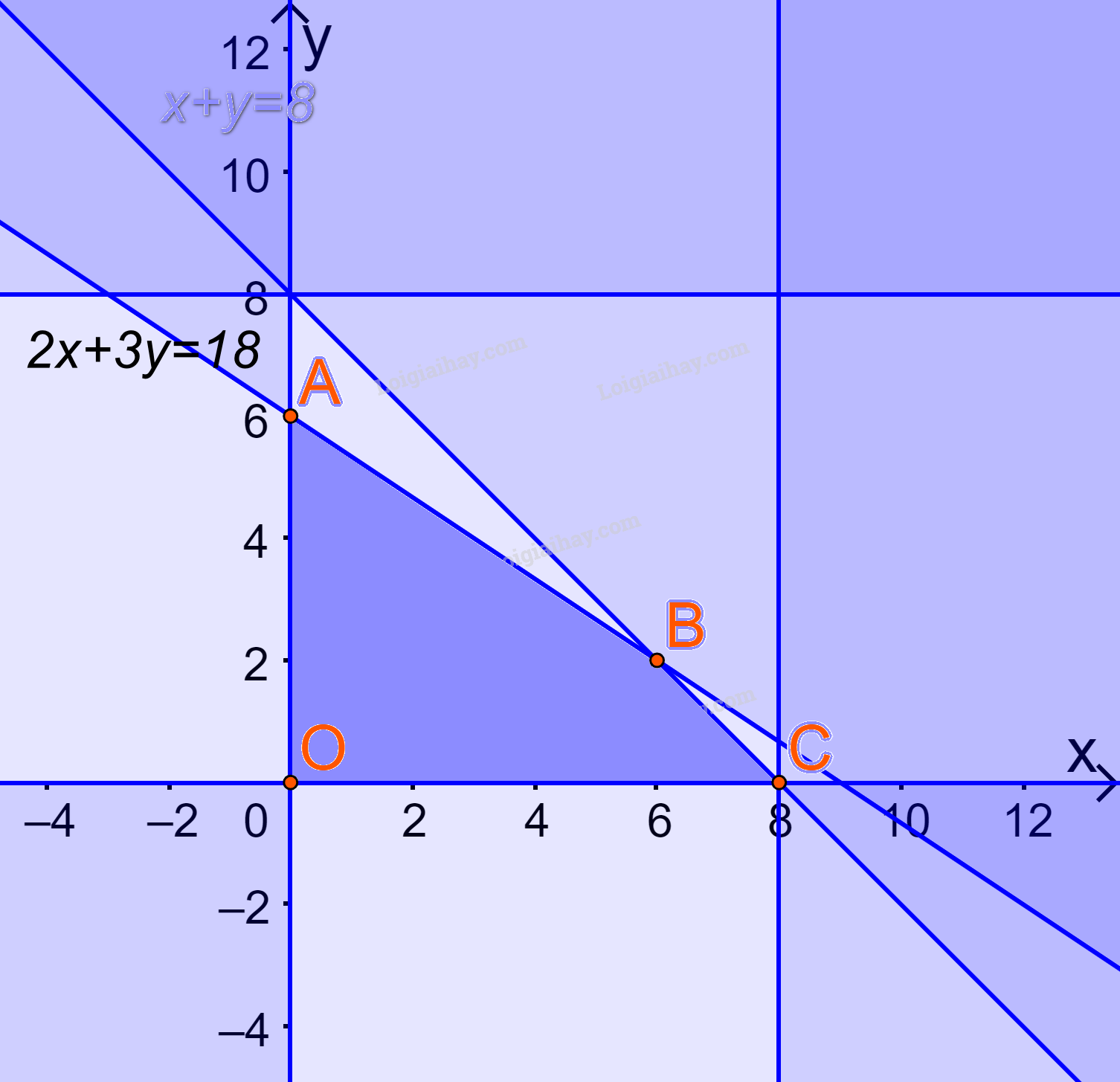
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh), trong đó \(A(0;6),B(6;2),C(8;0),O(0;0)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 300x + 400y\) ta được:
\[\begin{array}{l}F(0;0) = 300.0 + 400.0 = 0\\F(0;6) = 300.0 + 400.6 = 2400\\F(2;6) = 300.2 + 400.6 = 3000\\F(8;0) = 300.8 + 400.0 = 2400\end{array}\]
Do đó F đạt giá trị lớn nhất bằng 3000 tại \(x = 2;y = 6\)
Vậy cô Minh cần mua trồng \(2{m^2}\) cà chua và \(6{m^2}\) cải bắp.
Bài toán tìm giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của biểu thức F = ax + by trên một miền đa giác là một bài toán kinh điển trong chương trình Toán học, thường xuất hiện trong các kỳ thi THPT Quốc gia và các kỳ thi học sinh giỏi. Bài toán này có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ kinh tế đến kỹ thuật.
Để giải quyết bài toán này, chúng ta cần nắm vững một số kiến thức cơ bản:
Có hai phương pháp chính để giải bài toán này:
Phương pháp này dựa trên việc phân tích hình học của miền đa giác và tìm các điểm cực trị của biểu thức F = ax + by trên các đỉnh và cạnh của đa giác.
Phương pháp này dựa trên việc sử dụng các công cụ đại số để giải quyết bài toán.
Ví dụ: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = 2x + y trên miền đa giác giới hạn bởi các đường thẳng x = 0, y = 0, x + y = 4.
Giải:
Miền đa giác là tam giác OAB với A(4, 0), B(0, 4), O(0, 0).
Tính giá trị của F tại các đỉnh:
Xét các cạnh:
Vậy, giá trị lớn nhất của F là 8 tại điểm A(4, 0) và giá trị nhỏ nhất của F là 0 tại điểm O(0, 0).
Khi giải bài toán này, cần lưu ý:
Để củng cố kiến thức, bạn có thể thực hành với các bài tập sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về cách tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác. Chúc bạn học tập tốt!