Các phép toán trên tập hợp là một phần kiến thức cơ bản và vô cùng quan trọng trong chương trình Toán học, đặc biệt là ở cấp THPT. Việc nắm vững các phép toán này không chỉ giúp bạn giải quyết các bài toán cụ thể mà còn là nền tảng để tiếp cận các khái niệm toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, giúp bạn nắm vững kiến thức về các phép toán trên tập hợp một cách hiệu quả nhất.
(A cap B = { x|x in A) và (x in B} ) (A cup B = { x|x in A) hoặc (x in B} ) (A{rm{backslash }}B = { x in A|x notin B} )
1. Lý thuyết
+ Phép giao
Tập hợp gồm các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B. Kí hiệu: \(A \cap B\)
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
+ Phép hợp
Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B gọi là hợp của hai tập hợp A và B. Kí hiệu: \(A \cup B\)
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
+ Hiệu của A và B
Tập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B. Kí hiệu: \(A{\rm{\backslash }}B\).
\(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
+ Phần bù
Nếu \(A \subset B\) thì hiệu \(A{\rm{\backslash }}B\) gọi là phần bù của A trong B. Kí hiệu: \({C_B}A\)
+ Biểu đồ Ven
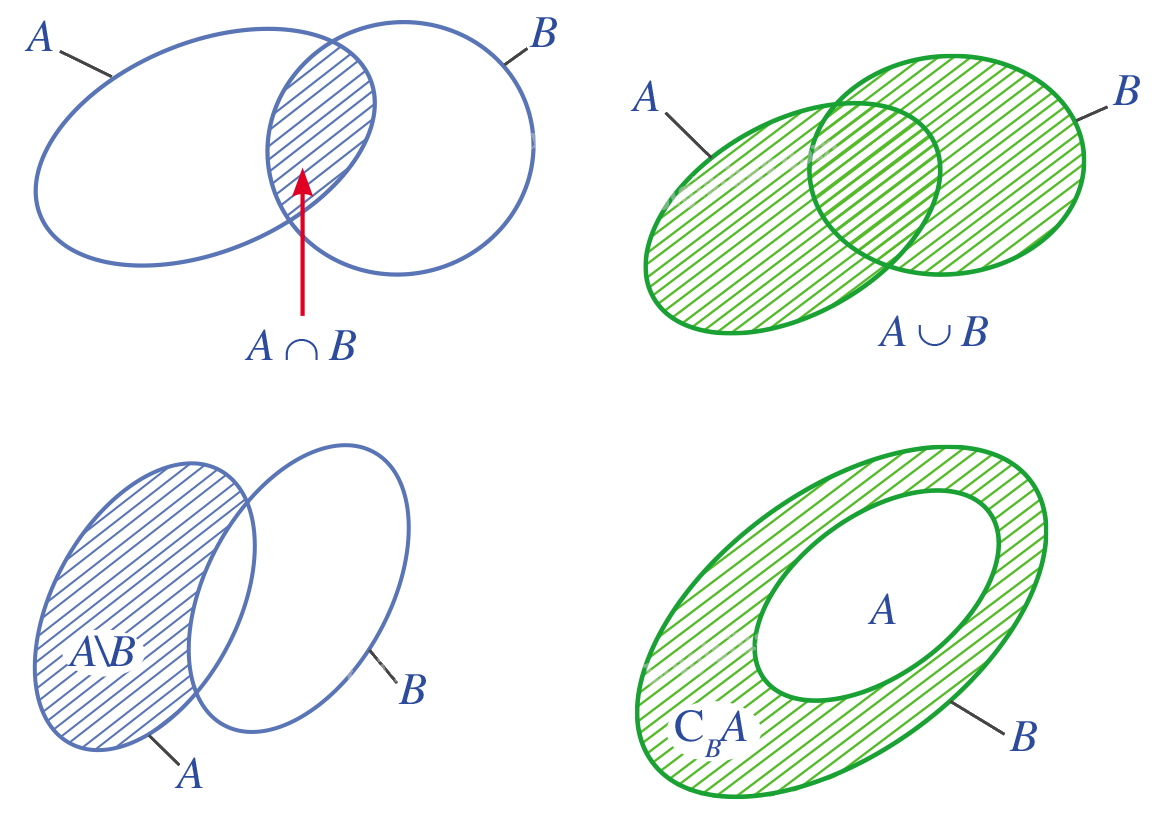
+ Mối quan hệ về số phần tử
\(n\left( {A \cup B} \right) = n(A) + n(B) - n(A \cap B)\)
\(n(A{\rm{\backslash }}B) = n(A) - n(A \cap B)\)
2. Ví dụ minh họa
Ví dụ 1. Cho hai tập hợp \(A = \left[ { - 2;{\mkern 1mu} {\mkern 1mu} 3} \right)\) và \(B = \left[ {1;6} \right)\).
Xác định các tập hợp \(A \cup B,A \cap B,A{\rm{\backslash }}B,B{\rm{\backslash }}A\)
\(A \cup B = [ - 2;6)\)

\(A \cap B = [ - 1;3)\)

\(A\backslash B = [ - 2; - 1)\)

\(B\backslash A = [3;6)\)

Ví dụ 2. Cho hai tập hợp \(A = ( - 1;4]\) và \(B = [ - 2; + \infty )\). Xác định tập hợp \({C_B}A\).
Ta có: \({C_B}A = B\backslash A = [ - 2; + \infty ){\rm{\backslash }}( - 1;4]\)

\( \Rightarrow {C_B}A = [ - 2; - 1] \cup (4; + \infty ).\)
Tập hợp là một khái niệm cơ bản trong toán học, dùng để chứa các đối tượng được xác định rõ ràng. Các đối tượng này, được gọi là các phần tử của tập hợp, có thể là bất kỳ thứ gì: số, người, hình dạng, hoặc thậm chí các tập hợp khác. Các phép toán trên tập hợp cho phép chúng ta kết hợp, so sánh và thao tác với các tập hợp để tạo ra các tập hợp mới.
Các phép toán trên tập hợp có rất nhiều ứng dụng trong các lĩnh vực khác nhau của toán học và khoa học máy tính:
Bài toán: Cho A = {a, b, c, d}, B = {b, d, e, f}. Hãy tìm A ∪ B, A ∩ B, A \ B và B \ A.
Giải:
Để nắm vững kiến thức về các phép toán trên tập hợp, bạn cần luyện tập thường xuyên với các bài tập khác nhau. Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống bài tập phong phú, được phân loại theo mức độ khó, giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán.
Các phép toán trên tập hợp là một công cụ mạnh mẽ và linh hoạt trong toán học. Việc hiểu rõ và nắm vững các phép toán này là rất quan trọng để thành công trong học tập và nghiên cứu toán học. Hãy bắt đầu hành trình khám phá thế giới tập hợp ngay hôm nay tại giaitoan.edu.vn!