Bài viết này sẽ cung cấp cho bạn kiến thức cơ bản và nâng cao về hàm số, đặc biệt tập trung vào "Cách cho một hàm số". Chúng ta sẽ cùng nhau khám phá định nghĩa, các dạng biểu diễn, và cách xác định hàm số một cách chính xác.
Tại giaitoan.edu.vn, chúng tôi luôn nỗ lực mang đến những tài liệu học toán online chất lượng, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.
Nếu với mỗi giá trị \(x\) thuộc tập D, ta xác định được một và chỉ một giá trị tương ứng thuộc tập hợp số thực \(\mathbb{R}\) thì ta có một hàm số.
1. Lý thuyết
+ Định nghĩa:
Nếu với mỗi giá trị \(x\) thuộc tập D, ta xác định được một và chỉ một giá trị tương ứng thuộc tập hợp số thực \(\mathbb{R}\) thì ta có một hàm số.
\( \Rightarrow \) Nếu với một giá trị của x mà ta tìm được từ 2 giá trị của y thì y không là hàm số của x.
+ Cách gọi: \(x\) là biến số, \(y\) là hàm số của \(x\).
+ Kí hiệu: Thường dùng \(y = f(x)\)
+ Cách cho một hàm số
Dạng bảng
Ví dụ: Dự báo thời tiết ngày 2/11/2022 tại Hà Nội
Giờ | 1 | 4 | 7 | 10 | 13 | 16 | 19 | 22 |
Nhiệt độ \({(^o}C)\) | 19 | 17 | 22 | 26 | 29 | 27 | 25 | 23 |
Dạng biểu đồ
Ví dụ: Dự báo thời tiết ngày 20/11/2021 tại Hà Nội
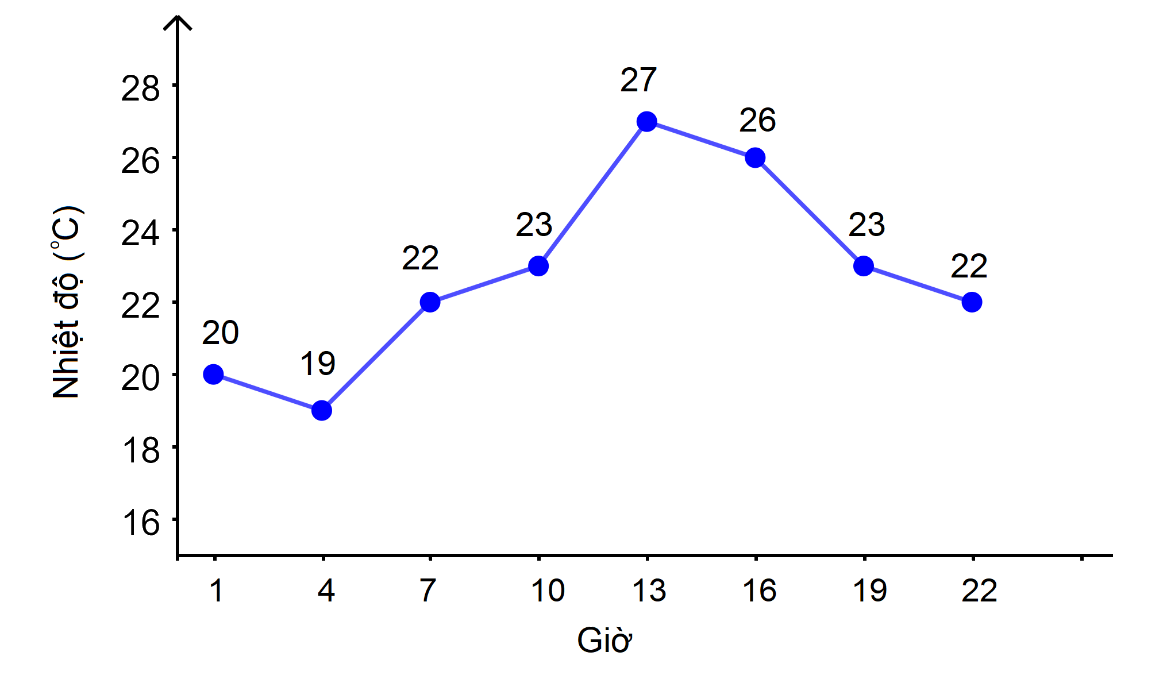
Dạng công thức
Một hàm số có thể được cho bởi một hoặc nhiều công thức.
Chẳng hạn:
\(y = {x^2} + 3\)
\(f(x) = \left\{ \begin{array}{l} - 3x + 5\quad \quad x \le 1\\2{x^2}\quad \quad \quad \;\;x > 1\end{array} \right.\)
2. Ví dụ minh họa
+ Hàm số
1. Bảng dưới đây biểu thị một hàm số
\(t\) (giây) | 1 | 2 | 4 | 6 | 9 |
\(v\) (mét/giây) | 2 | 3 | 0 | 5,5 | 7 |
\(v\) là một hàm số của \(t\) vì ứng với mỗi giá trị của t, có một và chỉ một giá trị tương ứng của v.
2. Hàm số cho bởi công thức
\(y = \sqrt x + 4\) với \(x \ge 0\)
\(f(x) = \left\{ \begin{array}{l}1\quad \quad \quad \;\;\quad \quad x \le 0\\2x - 1\quad \quad \quad 0 < x \le 5\\{x^2} - 3x - 1\quad \quad x > 5\end{array} \right.\)
+ Không là hàm số
a) Cho bảng sau
\(x\) | 1 | 0 | 2 | 1 | 5 |
\(y\) | 2 | 3 | 0 | -1 | 7 |
\(y\) không là hàm số của \(x\) vì với \(x = 1\) ta xác định được hai giá trị của y là \(y = 2\) và \(y = - 1\).
b) Cho \(x,y \in \mathbb{R}\) thỏa mãn: \({x^2} + {y^2} = 4\)
Khi đó \(y\) không là hàm số của \(x\) vì với \(x = 0\) ta xác định được hai giá trị \(y = 2\) và \(y = - 2\) đều thỏa mãn.
Hàm số là một quy tắc quan hệ giữa hai tập hợp, tập hợp đầu vào (tập xác định) và tập hợp đầu ra (tập giá trị). Nói cách khác, hàm số gán mỗi phần tử trong tập xác định với duy nhất một phần tử trong tập giá trị. Ký hiệu phổ biến của hàm số là f: A → B, trong đó A là tập xác định và B là tập giá trị.
Có nhiều cách để cho một hàm số:
Tập xác định (TXĐ) của hàm số là tập hợp tất cả các giá trị của x mà hàm số có nghĩa. Để tìm tập xác định, ta cần xác định các điều kiện để hàm số không xác định (ví dụ: mẫu số bằng 0, căn bậc chẵn của một số âm, logarit của một số không dương).
Tập giá trị (TGT) của hàm số là tập hợp tất cả các giá trị của f(x) mà hàm số có thể nhận được. Việc tìm tập giá trị thường khó khăn hơn tập xác định và đòi hỏi kiến thức về các tính chất của hàm số.
Ví dụ 1: Cho hàm số f(x) = 3x - 2. Hãy tìm tập xác định và tập giá trị của hàm số.
Giải:
Ví dụ 2: Cho hàm số f(x) = 1 / (x - 1). Hãy tìm tập xác định của hàm số.
Giải:
Hàm số xác định khi và chỉ khi mẫu số khác 0. Vậy x - 1 ≠ 0, suy ra x ≠ 1. Do đó, TXĐ = ℝ \ {1}.
Hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Hàm số là một khái niệm cơ bản và quan trọng trong toán học. Việc hiểu rõ định nghĩa, các cách cho hàm số, tập xác định, tập giá trị và các dạng hàm số phổ biến là nền tảng để học tập các kiến thức toán học nâng cao hơn. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về hàm số.