Trong quá trình học toán, chúng ta thường gặp những câu hỏi mang tính xác suất như 'Có thể xảy ra?', 'Chắc chắn xảy ra?', hay 'Không thể xảy ra?'. Việc hiểu rõ ý nghĩa của các khái niệm này là nền tảng quan trọng để giải quyết các bài toán liên quan đến xác suất và thống kê.
Giaitoan.edu.vn sẽ giúp bạn làm rõ những khái niệm này thông qua các bài giảng, bài tập thực hành và các ví dụ minh họa sinh động.
Giải Có thể, chắc chắn, không thể trang 105 SGK Toán 2 Chân trời sáng tạo. Bài 1. Có thể, chắc chắn hay không thế?
Bài 2 (trang 105 SGK Toán 2 tập 1)
Trò chơi Tập tầm vông (nhóm chơi 2 người).
• Người đố giấu  trong lòng một bàn tay và nắm lại rồi hát:
trong lòng một bàn tay và nắm lại rồi hát:
Tập tầm vông
Tay không tay có
Tập tầm vó
Tay có tay không
Tay nào có, tay nào không?
• Người đoán chỉ một tay của người đố.
Nếu đoán đúng, người đoán sẽ trở thành người đố, trò chơi lại tiếp tục.
Lời giải chi tiết:
Các em tự chơi theo hướng dẫn nhé.
Bài 1 (trang 105 SGK Toán 2 tập 1)
Có thể, chắc chắn hay không thể?
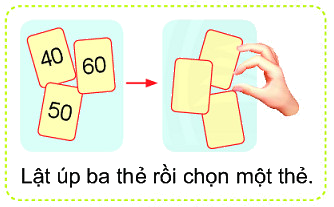
a) Thẻ được chọn .?. có số tròn chục.
b) Thẻ được chọn .?. có số 70.
c) Thẻ được chọn .?. có số 50.
Phương pháp giải:
- Quan sát các số đã cho rồi dự đoán các trường hợp có thể xảy ra.
- Số tròn chục là số có chữ số hàng đơn vị là 0.
Lời giải chi tiết:
a) Thẻ được chọn chắc chắn có số tròn chục (Vì các số 40, 50, 60 đều là số tròn chục).
b) Thẻ được chọn không thể có số 70 (Vì trong 3 thẻ không có thẻ nào có số 70).
c) Thẻ được chọn có thể có số 50 (Vì trong 3 thẻ có 1 thẻ có số 50).
Hoạt động thực tế (trang 105 SGK Toán 2 tập 1)
Em tập dùng các từ có thể, chắc chắn, không thể khi nói chuyện với người thân.
Lời giải chi tiết:
Ví dụ mẫu:
Em và anh chơi chơi trò tung xúc xắc với nhau.

Em tung xúc xắc 1 lần. Khi đó:
- Số chấm tròn trên mặt xúc xắc chắc chắn là số tự nhiên lớn hơn 0 và nhỏ hơn 7.
- Số chấm tròn trên mặt xúc xắc có thể là 4.
- Số chấm tròn trên mặt xúc xắc không thể là 8.
Bởi vì: xúc xắc có 6 mặt và số chấm tròn trên các mặt đó là 1; 2; 3; 4; 5; 6.
Bài 1 (trang 105 SGK Toán 2 tập 1)
Có thể, chắc chắn hay không thể?
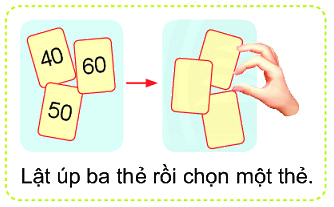
a) Thẻ được chọn .?. có số tròn chục.
b) Thẻ được chọn .?. có số 70.
c) Thẻ được chọn .?. có số 50.
Phương pháp giải:
- Quan sát các số đã cho rồi dự đoán các trường hợp có thể xảy ra.
- Số tròn chục là số có chữ số hàng đơn vị là 0.
Lời giải chi tiết:
a) Thẻ được chọn chắc chắn có số tròn chục (Vì các số 40, 50, 60 đều là số tròn chục).
b) Thẻ được chọn không thể có số 70 (Vì trong 3 thẻ không có thẻ nào có số 70).
c) Thẻ được chọn có thể có số 50 (Vì trong 3 thẻ có 1 thẻ có số 50).
Bài 2 (trang 105 SGK Toán 2 tập 1)
Trò chơi Tập tầm vông (nhóm chơi 2 người).
• Người đố giấu  trong lòng một bàn tay và nắm lại rồi hát:
trong lòng một bàn tay và nắm lại rồi hát:
Tập tầm vông
Tay không tay có
Tập tầm vó
Tay có tay không
Tay nào có, tay nào không?
• Người đoán chỉ một tay của người đố.
Nếu đoán đúng, người đoán sẽ trở thành người đố, trò chơi lại tiếp tục.
Lời giải chi tiết:
Các em tự chơi theo hướng dẫn nhé.
Hoạt động thực tế (trang 105 SGK Toán 2 tập 1)
Em tập dùng các từ có thể, chắc chắn, không thể khi nói chuyện với người thân.
Lời giải chi tiết:
Ví dụ mẫu:
Em và anh chơi chơi trò tung xúc xắc với nhau.

Em tung xúc xắc 1 lần. Khi đó:
- Số chấm tròn trên mặt xúc xắc chắc chắn là số tự nhiên lớn hơn 0 và nhỏ hơn 7.
- Số chấm tròn trên mặt xúc xắc có thể là 4.
- Số chấm tròn trên mặt xúc xắc không thể là 8.
Bởi vì: xúc xắc có 6 mặt và số chấm tròn trên các mặt đó là 1; 2; 3; 4; 5; 6.
Trong toán học, đặc biệt là trong lĩnh vực xác suất thống kê, việc phân loại các sự kiện dựa trên khả năng xảy ra của chúng là vô cùng quan trọng. Ba khái niệm cơ bản được sử dụng để mô tả khả năng này là 'có thể', 'chắc chắn' và 'không thể'.
Một sự kiện được gọi là 'có thể' nếu nó có khả năng xảy ra, nhưng không phải lúc nào cũng xảy ra. Nói cách khác, sự kiện này có thể xảy ra hoặc không xảy ra, tùy thuộc vào điều kiện cụ thể. Ví dụ:
Một sự kiện được gọi là 'chắc chắn' nếu nó luôn luôn xảy ra, bất kể điều kiện nào. Nói cách khác, sự kiện này không thể không xảy ra. Ví dụ:
Một sự kiện được gọi là 'không thể' nếu nó không bao giờ xảy ra, bất kể điều kiện nào. Nói cách khác, sự kiện này không có khả năng xảy ra. Ví dụ:
Hiểu rõ các khái niệm 'có thể', 'chắc chắn' và 'không thể' là rất quan trọng trong việc giải các bài toán về xác suất. Ví dụ, khi tính xác suất của một sự kiện, chúng ta cần xác định xem sự kiện đó có thể xảy ra hay không. Nếu sự kiện đó không thể xảy ra, xác suất của nó bằng 0. Nếu sự kiện đó chắc chắn xảy ra, xác suất của nó bằng 1.
Xét bài toán sau:
Một hộp chứa 5 quả bóng, trong đó có 3 quả bóng màu đỏ và 2 quả bóng màu xanh. Nếu chúng ta lấy ngẫu nhiên một quả bóng từ hộp, hãy tính xác suất để quả bóng đó màu đỏ.
Trong trường hợp này, sự kiện 'lấy được quả bóng màu đỏ' là một sự kiện có thể. Xác suất của sự kiện này được tính như sau:
P(đỏ) = Số quả bóng màu đỏ / Tổng số quả bóng = 3/5
Ngoài ba khái niệm cơ bản trên, còn có các khái niệm khác liên quan đến khả năng xảy ra của sự kiện, như 'gần như chắc chắn' và 'gần như không thể'. Tuy nhiên, ba khái niệm 'có thể', 'chắc chắn' và 'không thể' là nền tảng quan trọng nhất để hiểu về xác suất.
Giaitoan.edu.vn cung cấp một loạt các bài tập và tài liệu học tập giúp bạn nắm vững các khái niệm về xác suất và thống kê, bao gồm cả việc phân loại các sự kiện dựa trên khả năng xảy ra của chúng. Hãy truy cập giaitoan.edu.vn để bắt đầu hành trình khám phá thế giới toán học đầy thú vị!
| Khái Niệm | Mô Tả | Ví Dụ |
|---|---|---|
| Có Thể | Sự kiện có khả năng xảy ra, nhưng không phải lúc nào cũng xảy ra. | Tung đồng xu được mặt ngửa. |
| Chắc Chắn | Sự kiện luôn luôn xảy ra. | Mặt trời mọc ở hướng Đông. |
| Không Thể | Sự kiện không bao giờ xảy ra. | Rút lá bài có giá trị lớn hơn 13. |
Việc hiểu rõ các khái niệm 'có thể', 'chắc chắn' và 'không thể' là bước đầu tiên quan trọng để làm chủ môn toán học, đặc biệt là trong lĩnh vực xác suất và thống kê. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức.